基于混沌-粒子群算法的柔性线缆装配序列规划技术

杨啸东， 刘检华， 马江涛， 赵瑛峰， 吕乃静

(北京理工大学 机械与车辆学院 数字化制造研究所，北京 100081)

装配序列规划(assembly sequence planning，ASP)是指寻求一组较优的序列使得待装配零部件组装在一起. ASP是产品装配工艺规划的核心环节，在产品质量、装配效率以及产品的全生命周期中起到关键作用，其优劣将直接影响到产品的装配质量. 但是，目前复杂机电产品的装配工艺规划尚存在不足，其装配序列自动规划通常仅考虑刚性结构件，柔性线缆的装配规划仍以模装法和模板法为主，大量依赖物理样机和操作工人的经验，线缆的装配序列规划问题已经成为复杂机电产品装配序列规划中的瓶颈难题[1-3].

当前常见的装配序列规划方法有人机交互法、几何可行推理法、基于知识的推理方法和智能优化算法[4]. 由于装配序列规划是一个典型的非确定多项式(NP)问题，利用智能优化算法通常可以得到这类问题的较优解. 常见的智能优化算法有遗传算法、蚁群算法、粒子群算法、模拟退火算法、萤火虫算法等. Murali等[5]通过模拟退火算法来解决减速箱的装配序列规划问题，Wang等[6]基于遗传-蚁群混合算法对反射板进行了装配序列规划，吴宏超等[7]提出了一种基于萤火虫算法的管路布局序列优化方法，相对而言，粒子群算法是一种易于编码的群智能优化算法，其全局搜索能力强，收敛速度快，同时比较容易实现，因此也越来越多地用来求解这类问题，如Wu等[8]通过粒子群算法解决了偏心铣床的装配序列规划问题，与遗传算法相比，该算法的收敛速度更快，效率更高.

上述研究存在的主要问题在于假设待装配的零部件都是刚体，即在装配过程中不会发生变形，但复杂机电产品中柔性线缆的装配占据了大量的比重，且线缆不同于刚性零部件，具有布局密集、长径比大、弯角多、分支结构复杂等特点，这也为线缆装配序列规划的研究增加了困难. Somayé等[9]通过柔性件的装配干涉矩阵和装配应力矩阵，从几何、物理、机械等方面定义了其装配性能，但并未提出柔性线缆装配序列规划的具体方法. 为解决线缆序列规划难题，笔者提出了一种基于改进粒子群算法的柔性线缆装配序列规划方法，该方法综合考虑了线缆上述特点，并通过实例分析和算法对比验证了所提算法的可行性及效率.

1 线缆装配序列规划数学模型

针对柔性线缆装配序列规划问题，需要建立相应的数学模型. 笔者首先根据线缆装配序列规划的影响因素确定其约束条件，然后在此基础上建立该过程的优化目标.

1.1 约束条件的确定

在实际布线过程中，先敷设的线缆将会直接影响到后续线缆的敷设空间，因此整机的线缆装配顺序对产品的布线成功率具有重要影响. 线缆装配顺序一般要服从的约束条件为：①先敷设布局密集的线缆，后敷设布局稀疏的线缆；②先敷设直径和弯曲半径大的线缆，后敷设直径和弯曲半径小的线缆；③先敷设多分支线缆，后敷设单分支线缆. 其中①为考虑线缆装配的优先级约束，即满足可装配性与装配可达性的要求，若先敷设布局稀疏的线缆，则本身布局密集的线缆的装配空间将会进一步受到制约，甚至无法完成装配；第②③则是考虑线缆敷设路径的几何复杂性. 线缆装配序列的优化目标也将依据①②③中的约束条件设计.

1.2 优化目标的建立

1.2.1适应度函数影响因子的确定

根据上述的约束条件，确定以线缆装配优先级、线缆长度、直径、弯曲半径和线缆分支数为设计变量，即目标函数(适应度函数)的影响因子. 其中，线缆装配优先等级系数P由线缆布局密度δ(δ为每平方米的线缆数目)决定. 线缆布局越密集的区域，装配优先等级越高，二者的对应关系如表1所示. 数值越小则对应区域内线缆的装配优先等级越高.

表1 线缆布局密度与装配优先等级系数的对应关系

1.2.2适应度函数的构造

适应度函数的构造对线缆装配序列优劣的评判具有重要作用，由上述的布线约束条件可知，本文目标函数为最大值问题，即适应度值越高，其对应的装配序列性能越好. 根据1.1节的影响因素进行适应度函数的构造，包括线缆装配优先等级系数P、长度L、直径D、弯曲半径R、分支数S这几方面，以下将详细说明.

① 线缆装配优先等级系数P.

f1表示线缆装配优先等级系数P对适应度函数的影响因子. 通常情况下，最优装配序列中最先装配完成的线缆，其装配优先等级系数P是最小的(优先等级高的线缆要先完成装配)，即Xi[1].P=1. 且随着装配先后次序的递增，线缆装配优先等级系数P总体上应呈递增趋势，即Xi[j].P≤Xi[j+1].P，其中1≤j≤n-1，n为线缆总数(若某支线缆为跨装配单元装配，即线缆不同部位对应的装配优先级系数不同，则该线缆的装配优先级系数取其中的最小值，但在实际装配过程中，非跨装配单元的线缆优先于相同优先等级系数跨装配单元的线缆完成装配).

综合上述情况，f1的表达式为

(1)

② 线缆长度L*线缆直径D*弯曲半径R.

f2表示线缆长度L*线缆直径D*弯曲半径R对适应度函数的影响因子(同一支线缆中的多个弯曲半径，取其中最大值). 一般来说，粗长且弯角大的线束的装配要优先于细短且弯角小的线束.

综合上述情况，f2的表达式为

f2=

(2)

③ 线缆分支数S.

f3表示线缆分支数S对适应度函数的影响因子. 一般来说，分支数大的线缆的装配要优先于分支数小的线缆.

综合上述情况，f3的表达式为

(3)

综合考虑线缆装配序列的可行性、线缆装配优先等级P,线缆长度L*线缆直径D*弯曲半径R、线缆分支数S，确定适应度函数如下(w1、w2、w3为三个影响因素的权重系数)：

fitness(n)=

(4)

式中：n为线缆的总数；f1、f2、f3的初始值均为0；wi(1≤i≤3)为这三个影响因子的权重系数，且满足：

(5)

2 标准粒子群算法原理

2.1 粒子群算法概述

标准PSO算法的速度和位置更新公式为

Vi(t+1)=ωVi(t)+c1rand()×

[Pbesti-Xi(t)]+c2rand()×

[Gbesti-Xi(t)],

(6)

Xi(t+1)=Xi(t)+Vi(t+1),

(7)

式中:Pbesti为当前粒子i找到的最优解；Gbesti为当前在整个种群中找到的全局最优解；Vi(t)和Xi(t)分别代表粒子i在第t次迭代中的速度和位置;ω为非负惯性权重(惯性因子)，决定了对粒子当前速度的继承比例，其作用是保持粒子群体扩展搜索空间的能力;参数c1和c2是用以调整粒子运动过程中的局部搜索能力与全局搜索能力学习因子，其中学习因子c1反映了个体历史最优位置对更新速度Vi(t+1)的影响，学习因子c2反映了全局最优位置对更新速度Vi(t+1)的影响.

2.2 线缆装配序列规划与PSO模型的对应关系

对于PSO算法，编码方式、位置更新与速度更新需要离散化处理，因此线缆装配序列规划问题的模型可通过以下关系与PSO模型对应起来.

① 编码方式：采用实数编码的方式，设第i支线缆的编号为xi，xi∈[1,n]，则X=[x1x2…xn]为解的一般形式. 序列中的元素与线缆编号一一对应，如{2,5,1,7,3,9,10,8,6,4}，其结构示意图如图1所示.

② 粒子i的位置：粒子i的位置对应于线缆装配序列的一组有序排列，每个粒子的位置初始化为一个n维矢量，即Xi=[xi1xi2…xij…xin]，其中xij∈{1,2…,n}，n为机电产品中线缆总数.

③ 粒子i的速度：粒子的速度对应粒子位置的改变，粒子i位置的改变即线缆装配序列i排列顺序的一种变换序列，装配序列i的速度矢量表示如下：Vi=[vi1vi2…vij…vin]，其中vij∈{1,2,3,…,n}，vij表示粒子i速度矢量的第j维分量且算法的初始速度随机生成.

由于惯性权重ω与学习因子c1和c2对PSO算法的性能有很大程度的影响，同时为提高粒子的自我总结和向群体中精英个体学习的能力，需要重新定义上述公式中的ω、c1和c2. 此处的惯性权重ω与学习因子c1和c2均为变量，其定义如下：

(8)

式中：ωmax和ωmin为设定的惯性权重的最大值与最小值，其值分别为ωmax=0.9，ωmin=0.3；Gmax为最大迭代次数；n为已迭代次数；c1l、c1s、c2l、c2s分别为学习因子c1和c2在PSO中的最大值与最小值，其中，c1l=0.8，c1s=0.2，c2l=0.2，c2s=0.8. 式(8)重新定义的优点在于算法迭代早期避免了粒子陷入局部最优，迭代后期有利于算法的快速收敛.

3 粒子群算法的改进

由于标准PSO算法的初始解是随机生成的，搜索寻优的过程也是随机的，这会浪费粒子群的搜索时间，降低优化的效率，同时容易陷入局部最优解. 为克服以上缺点，需要对PSO算法的初始化和搜索策略进行改进. 本文提出装配优先关系矩阵的概念，对装配序列的初始化进行改进，同时引入混沌算法来确定线缆的交换位置，改进了算法的搜索策略.

3.1 PSO算法的初始化改进

3.1.1装配优先关系矩阵的生成

本文通过引入装配优先关系矩阵APM(assembly priority matrix，APM)，来改进PSO算法的初始化.

装配优先关系矩阵由一个n维矩阵APM=[aij](1 ≤i,j≤n)表示，其中n为机电产品中线缆的数量，对APM中的元素aij做如下规定：

如果aii= 3，则第i支线缆为非跨装配单元线缆；

如果aii= 2，则第i支线缆为跨装配单元线缆；

如果aij= 0(i≠j)，则第i支线缆可以优先于第j支线缆进行装配；

如果aij= 1(i≠j)，则第i支线缆不可以优先于第j支线缆进行装配.

以表2中6支线缆为例，对APM的建立进行说明.

表2 线缆装配优先级基本信息

则APM为

3.1.2初始种群生成方法的改进

初始种群(即初始的线缆装配序列)生成方法的改进是指根据上述的APM求解出一些可行的线缆装配序列作为初始种群，以降低初始化的随机性与盲目性，提高粒子的搜索效率. 初始种群改进算法(IPSO)的流程图如图2所示，相应步骤如下：

① 遍历APM，找出符合所有aij=0(i≠j) 的行，加入到集合T1中；

② 遍历步骤①得到的集合T1，并将集合T1中满足aii= 3(非跨装配单元的线缆)的行序号i加入到集合T2中，将满足aii= 2(跨装配单元的线缆)的行序号i加入到集合T3中；

③ 若T2非空，则从集合T2中随机选择一个元素，例如p，在APM中删除p行、p列的所有元素，更新APM并将p记录到线缆装配序列集合T4中；若T2为空，则从集合T3中随机选择一个元素，例如q，在APM中删除q行、q列的所有元素，更新APM并将q记录到线缆装配序列集合T4中；

④ 重复步骤①到③，直至APM为空；

⑤ 将线缆装配序列集合T4中元素的顺序作为可行的初始化线缆装配序列.

3.2 PSO算法搜索策略的改进

3.2.1混沌算法的引入及作用

PSO算法优化成功的关键是具有持续发现最优解的能力. 标准PSO算法在每一次迭代寻优的过程中，粒子通过随机搜索发现下一个最优解，因此在整个优化过程中会产生大量重复解，浪费了粒子群的搜索时间；如果不能发现更好的最优解，算法就会陷入局部最优. 为解决粒子搜索过程中的问题，在改进PSO算法初始化的基础上，进一步引入混沌算法，以增加粒子个体的多样性和持续发现最优解的能力.

3.2.2基于混沌-粒子群算法的线缆装配序列规划

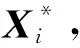
步骤1 确定混沌算法的发生机制. 选择下式所示的logistic映射作为混沌发生机制，其中μ是控制参量，称为吸引子. 当取μ=4且xk∉{0,0.25,0.50,0.75,1.00}时，确定性等式表现出混沌动态性，混沌变量初始值的微小变化会导致长期显著的变化，混沌变量的轨迹可以遍历优化问题的整个搜索空间.

xk+1=μxk(1-xk),xk∈(0,1).

(9)

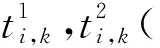
步骤3 按照给定的交换概率q交换装配序列Xi,k中ui,k+1，wi,k+1位置的线缆，得到新的装配序列Xi,k+1.

4 实例验证与算法比较

为验证上述算法的可行性及效率，对算法进行了实例测试. 系统的CPU为2.80 GHz Intel Core i5-2300，显卡为NVIDIA GeForceGT 240，内存4 GB，操作系统为Window 7 SP1，利用Matlab与C++的混合编程实现算法集成. 以图3所示

卫星结构板(包含10支多分支线缆，线缆编号如图所示)为例进行计算实例分析，其中结构件与线缆的建模均在CATIA软件中完成，提取的线缆参数信息如表3所示.

表3 线缆参数信息表

由于粒子数目越多，个体多样性越明显且越容易收敛到全局最优，为此，分别对PSO、IPSO、C-IPSO算法进行不同粒子数目下的实验. 算法参数设置如下：CNum=10，最大迭代次数为500，设定交换概率q=0.8，粒子数目分别为100，300，500，测试10次取平均值后得到的实验结果如表4所示，当粒子数目为500时得到的迭代收敛曲线对比如图4所示，最终得到的最优装配序列为7-2-10-8-4-3-1-9-5-6，最大适应度值为33.6.

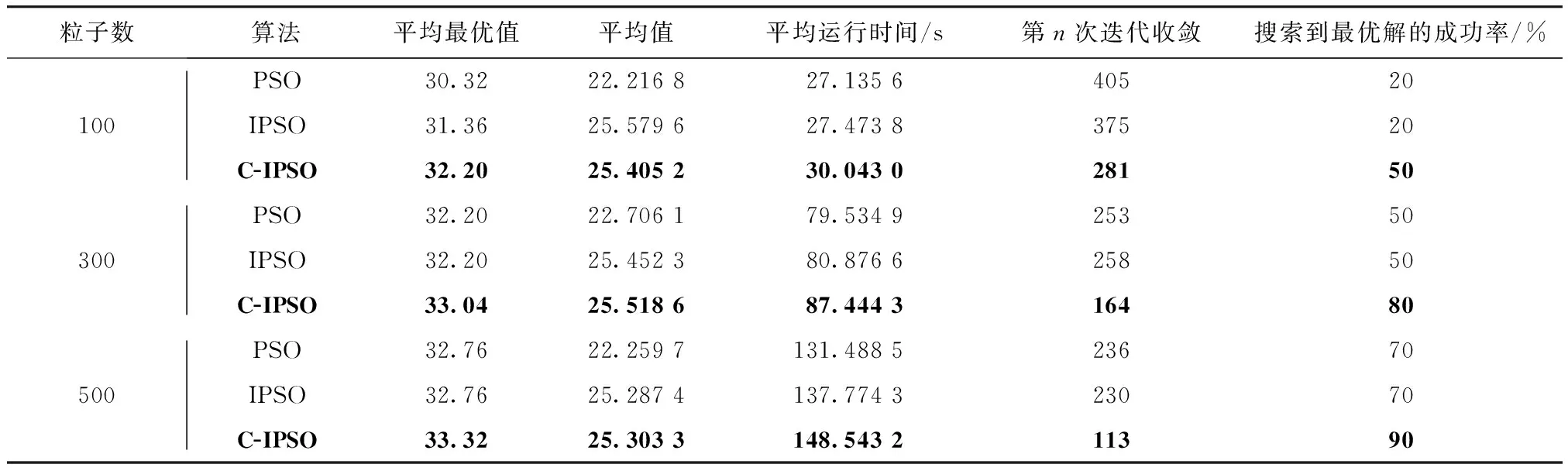
表4 实验结果对比

从表4的平均值对比中可看出，IPSO和C-IPSO算法的平均值较PSO算法有明显提升；从收敛速度和搜索到最优解的成功率可看出，C-IPSO算法的收敛速度和收敛到全局最优的概率明显优于PSO和IPSO算法. 从图4中可看出，IPSO和C-IPSO算法的初始值明显高于PSO算法的初始值，且C-IPSO算法的迭代收敛速度要快于IPSO和PSO算法. 因此，C-IPSO算法不仅改进了初始化的结果，同时提升了PSO算法的全局优化能力，加快了收敛速度. 从工程应用角度来看，C-IPSO算法得到的装配序列结果可用于指导并优化卫星结构板中线缆的装配工作，具有实际的工程意义.

5 结束语

针对复杂机电产品中线缆装配序列规划问题，引入粒子群算法，通过提出APM的概念对标准粒子群算法的初始化加以改进，通过引入混沌算法提高算法的搜索效率，并以卫星结构板中线缆的敷设为例进行了实例验证，反映出所提算法的可行性与稳定性，为线缆装配序列的优化提供了指导. 本文所述研究实现了线缆的装配序列规划，但复杂机电产品的实际装配通常是刚性零件与柔性线缆交叉装配的过程，因此如何确定刚柔混合的装配序列将会是后续研究的重点工作.