多MEMS监测系统温度补偿及在猴子岩大坝应用

郑天翱 蔡德所 陈声震

摘 要：多MEMS监测系统是高面板堆石坝安全监测的新技术。在实际监测中，由于运行管道内外存在温差，会使MEMS陀螺仪产生温度漂移，影响测量结果的精确度。为了抑制温度漂移对陀螺仪输出结果的影响，通过室内温度特性试验总结出MEMS陀螺仪的温度漂移规律，在此基础上，建立了基于回归理论的最小二乘法多项式温度补偿模型与一阶马氏链温度补偿模型，在猴子岩面板堆石坝的应用结果表明：两种方法均能有效降低陀螺仪的零偏误差，马氏链模型补偿效果优于多项式拟合模型的，精确度更高，能更好反映面板挠度和堆石体沉降的变形情况，可为大坝运行安全评价提供可靠依据。

关键词：大坝安全监测;MEMS陀螺仪;温度补偿;多项式拟合;马氏链

中图分类号：TV168.1 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.05.031

Abstract： Multi-MEMS monitoring system is a new technology for safety monitoring of high-panel rockfill dams. In actual monitoring， due to the temperature difference between the inside and outside of theoperational pipeline， the MEMS gyroscope will drift and affect the measurement accuracy. In order to suppress the influence of temperature drift on the output of gyroscope， the temperature drift law of MEMS gyroscope was summarized by the experiment of indoor temperature characteristics. On the basis of this， a least squares polynomial compensation model based on regression theory and first-order Markov chain compensation were established. The model was compensated by two methods. The results show that both methods can effectively reduce the yoke zero-bias stability and the Markov chain model has higher compensation accuracy which can better reflect the deflection of the panel and the deformation of the rockfill settlement. It also can provide a reliable basis for safety assessment of dam operations.

Key words： dam safety monitoring; MEMS gyroscope; temperature compensation; polynomial fitting; Markov chain

隨着我国面板堆石坝筑坝高度不断增高，逐渐从200 m级向300 m级坝高迈进，超高面板堆石坝的安全性受到人们的极大关注[1]。大坝变形监测可以及时掌握坝体内部性态的变化，为大坝在施工期及蓄水运行期的安全提供保障。面板堆石坝安全监测的两个必测项目是面板挠度和堆石体沉降。目前常规监测手段有采用引张线式水平位移计、水管式沉降仪和固定式测斜仪等仪器进行监测，均为点式监测，存在受施工干扰大、耐久性差、无法反映坝体最大变形量等问题，已无法满足现代化监测的要求[2]。多MEMS监测系统是在光纤陀螺仪基础上开发的新技术，具有全分布式、精确度高和稳定性好等优点，已成功应用于水布垭面板堆石坝（坝高233.0 m）、猴子岩面板堆石坝（坝高223.5 m）和江坪河面板堆石坝（坝高219.0 m）的变形监测，为大坝安全性评估提供了可靠的监测资料[3-5]。

多MEMS监测系统是利用事先在坝体内部埋设好的运行管道，通过采集

内置九轴MEMS传感器的监测小车在行走过程中的三维姿态，利用恒定的地磁场和重力场解算出监测小车在管道内的运行轨迹，进而得到坝体在该测线上的变形量[6]。在实际监测过程中，运行管道内外温差较大，导致多MEMS监测系统的核心部件三轴MEMS陀螺仪产生温度漂移，影响监测到的角速度信号的精确度，从而干扰整个系统的稳定性和准确性，所以对MEMS陀螺仪进行温度补偿至关重要。多MEMS监测系统的温度补偿，一般可以采取两种方式[7]：一是增加温控设施，或通过温控电路来降低硬件的温度，但会增加测量系统的体积;二是通过分析温度误差特性，针对温度误差漂移规律，建立实时温度误差补偿模型进行温度补偿，从而提高MEMS陀螺仪的精确度。相对于硬件补偿，建立温度误差补偿模型进行温度补偿的方法更加简单且实用有效。

1 MEMS陀螺仪温度特性试验

多MEMS传感器监测小车内置三轴磁通门传感器、三轴MEMS陀螺仪和三轴加速度计，其中三轴MEMS陀螺仪的主要材料为硅，为一种热敏材料，受温度变化影响很大。当微型陀螺仪壳体内装有测控电路或构成惯性组合时，因壳体密封而散热不良，电路的功耗使壳体内部温度急剧升高，导致微型陀螺仪工作环境急剧恶化，温度的剧烈变化影响MEMS陀螺仪的输出精度。

1.1 MEMS陀螺仪温度特性试验过程

MEMS陀螺仪的输出值与温度有很大关系[8]，为进一步了解它们之间的联系，进行MEMS陀螺仪室内温度特性试验，试验设备包括室内试验转台、VG910型温度控制箱、单轴位置速率转台。试验步骤：①将MEMS陀螺仪置于VG910型温度控制箱中，整体置于转台上，起始温度设置为18 ℃，接通电源后充分预热30 min;②将试验上限温度设置为38 ℃（模拟实际工程测量环境），MEMS陀螺仪和温度传感器采样间隔均为1 s，记录陀螺仪的输出值，同时通过安装在MEMS陀螺仪内的温度传感器记录实时温度;③重复以上步骤，并观察MEMS陀螺仪的输出值，比较不同温度下的值获得温度特性。

1.2 试验数据分析

通过陀螺仪内的温度传感器得到陀螺仪内部的温度变化曲线（见图1），通过计算机实时获得陀螺仪的输出值曲线（见图2）。

由图1可以看出，MEMS陀螺仪内部温度在预先设置的温度区间内，说明试验过程中保溫时间符合要求。由图2可以看出，在MEMS陀螺仪没有任何输入的情况下即产生了一定输出，这个输出值就是陀螺仪的漂移，并且陀螺仪的漂移呈增大趋势，这是陀螺仪内部材料的热稳定性发生了改变，进而影响了MEMS陀螺仪的性能以及监测的精确度。

2 MEMS陀螺仪温度误差补偿模型

2.1 多项式拟合模型的确定

2.1.1 多项式拟合模型阶次的确定

运用多项式拟合方法对MEMS陀螺仪温度漂移进行拟合时，往往要考虑模型阶次选择问题。模型的阶次越高，拟合的精确度越高，但是增加了计算量[9-10]，因此模型阶次选择既要考虑模型精确度，又要使计算简便。

当建立的m阶次模型的残差与m-1阶次模型的残差相近，且残差接近于0时，则无需再增加模型阶次，此时模型的精确度已满足要求。其中，残差指的是实际观测值y与回归方程计算值之差，残差εi可以看成是误差项ei的估计值。

以图1温度特性试验数据为例，分别对其建立1～8阶多项式模型，求出不同模型阶次的温度补偿残差。模型阶数为1、2、…、8时各模型残差分别为0.032 25、0.023 57、0.015 74、0.014 27、0.013 98、0.013 57、0.013 15、0.012 9。当模型阶次为1～3时，各模型残差较大，而在模型阶次为4～8时，模型残差与模型阶次关系逐渐稳定，且在阶次为4以后，残差变化很小，表明当模型阶次为4时，所建立的温度漂移模型已满足MEMS陀螺仪的精度要求。

2.1.2 多项式模型数据拟合结果

4阶多项式模型拟合曲线见图3，由图3可以看出，拟合曲线与MEMS陀螺仪原始输出曲线的整体趋势基本相同。

2.1.3 多项式拟合模型对MEMS陀螺仪温度误差补偿结果

采用多项式拟合模型对MEMS陀螺仪试验数据进行温度漂移补偿，补偿结果见图4。从图4可以看出，在温度变化的情况下，MEMS陀螺仪漂移极其不稳定，波动比较大，而经过建立的多项式拟合模型补偿后，MEMS陀螺仪的温度漂移显著降低，且相对稳定。在试验温度（18 ℃）下，MEMS陀螺仪的零偏稳定性为1.527 3 °/h，经过模型补偿后，降到了0.237 2 °/h，表明多项式拟合模型可以提高MEMS陀螺仪的精确度，同时说明该模型温度补偿简单实用，实时性好。但是该模型在精确度要求很高的条件下不太适用，而且采用该方法进行温度补偿后，陀螺仪的输出还会随温度发生一定程度的漂移。

2.2 马氏链

马尔可夫链简称马氏链，又称离散时间马氏链，是从一种状态向另一种状态的随机转换过程，这个过程需要具有“无记忆”的特性：下一个状态的概率分布只能由当前状态决定，之前的事件在时间序列中与它无关。马氏链作为实际过程的统计模型具有许多应用[10-11]。

在马氏链的每一步，系统可以根据概率分布从一种状态向另一种状态变化，也可以保持当前状态不变。这个状态变化称为转移，与不同状态变化相关的概率称为转移概率。随机游走是马氏链的一个例子。随机游走中每个步骤的状态是图中的一个点，每个步骤都可以移动到任何相邻的点，其中移动到各个点的概率是相同的[12-14]。在离散空间为F中的一个随机序列{X（n）|n=0，1，2，…}，如果在任意时刻m，以及任意的状态i1、i2、…、in、i、 j，满足：

2.2.2 马氏链对MEMS陀螺仪温度误差补偿结果

工程上常采用蒙特卡洛方法处理马氏链问题，其基本思想是运用随机数算法来解决某种事件出现的概率问题。简单来说就是通过随机抽样的方法得到随机变量的平均值，并近似作为问题的解。

首先在系统状态量中选取m个元素，控制量选取n个元素，即状态转移概率Pijk确定为n×m×m维。然后对温度模型进行抽样，在抽样过程中下一个状态值由蒙特卡洛方法确定。期望分布随机值的生成采用均匀分布发生器的功能转换，经过式（10）、式（11）输入和输出转换为马尔可夫状态：

计算出F（y）、F（x）就可以得到马氏链的拟合曲线，见图5。从图3和图5可以看出，马氏链拟合曲线相对于4阶多项式模型拟合曲线更加贴近于原始数据的趋势，说明马氏链的拟合精确度更高。将马氏链拟合后的数据代入式（9）温度补偿模型可以得到温度误差补偿后的陀螺仪输出值，见图6。

从图6可以看出，在温度变化的情况下，MEMS陀螺仪漂移极不稳定，波动较大，而通过建立的马氏链模型补偿后，陀螺仪零偏输出趋于平稳，且变化幅度显著减小。补偿后MEMS陀螺仪的漂移比较稳定，不会随温度、时间的变化而变化，基本稳定在0附近。在试验温度（18 ℃）下，MEMS陀螺仪的零偏稳定性为1.527 3°/h，经过马氏链模型补偿后的零偏稳定性降到了0.125 8°/h。

当温度为20、25、30 ℃时，马氏链模型的误差方差为4.30×10-4、5.60×10-4、3.70×10-4，4阶多项式模型的误差方差为1.30×10-3、1.60×10-3、1.90×10-3，马氏链的误差方差比多项式的误差方差要小得多，即马氏链模型的拟合效果更好。多项式模型相对于马氏链模型温度补偿误差要大，但是计算简便，运行速度快，因此在实际工程应用中，可以根据监测的精度要求选择计算模型。

3 工程应用

猴子岩水电站位于四川省甘孜藏族自治州康定市孔玉乡，是大渡河干流上第9个梯级电站。猴子岩混凝土面板堆石坝是世界上同类型的第二高坝[15]，坝高223.5 m，坝顶高程1 848.5 m，坝顶宽14.00 m，坝顶长278.35 m，大坝上游坝坡坡比为1∶1.4，下游坝坡综合坡比为1∶1.65。工程共布置了5条监测系统运行管道，以0+117.5断面面板挠度、0+162.8断面1 775 m高程坝体沉降监测为例，在面板挠度监测管道部位埋设安装了测斜仪，在坝体沉降监测管道部位安装了水管式沉降仪，以供对比分析，相互校核。

3.1 MEMS陀螺仪温度补偿

以第8次监测结果为例进行分析，此时坝顶高程1 848.5 m，坝前水位1 837.0 m。面板挠度管道沿着面板铺设，坝体沉降管道水平埋设在坝体内部，实际监测时MEMS陀螺仪温度变化曲线见图7、图8。

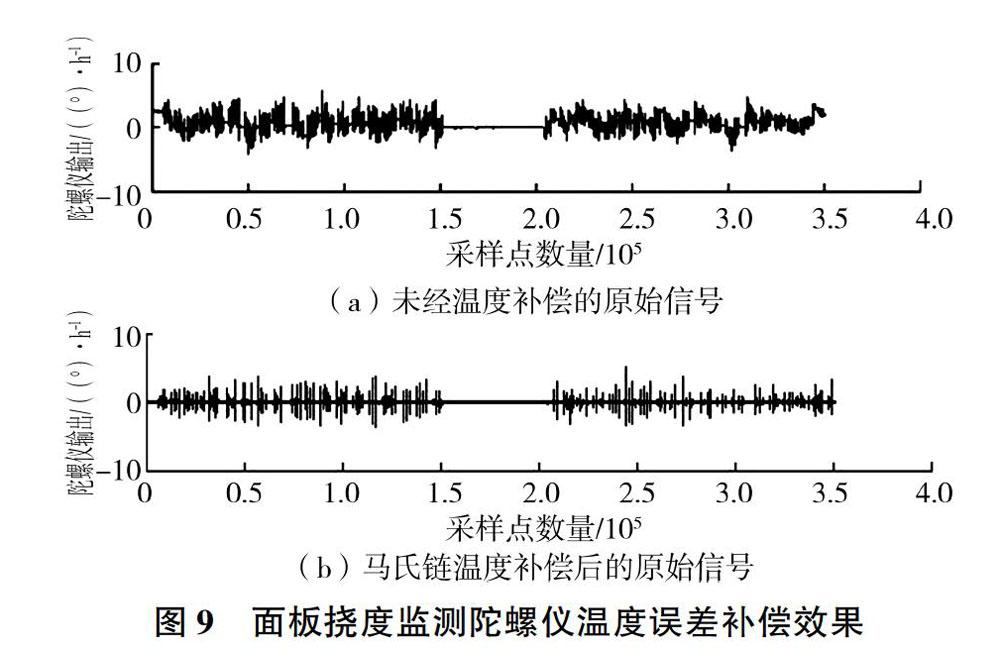
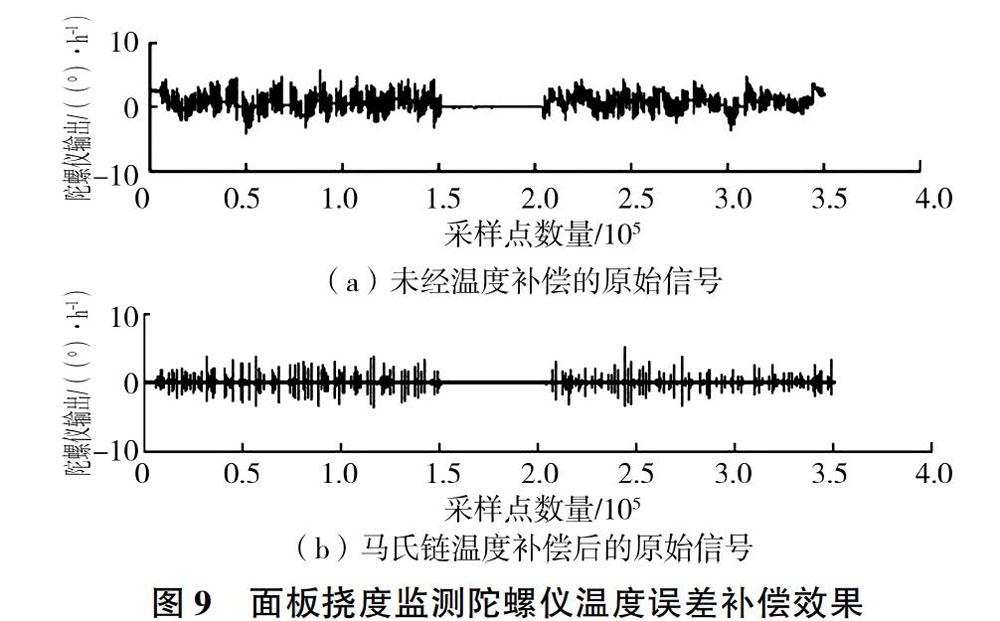
从图7可以看出，在面板挠度运行管道中MEMS陀螺仪温度缓慢上升至15.2 ℃。从图8可以看出，坝体沉降监测运行管道中MEMS陀螺仪温度先由12.4 ℃上升至13.2 ℃，再缓慢下降到11.3 ℃。MEMS陀螺仪温度大致与监测时的外部温度相近。采用精度更高的马氏链温度补偿模型对MEMS陀螺仪的信号进行实时处理，温度补偿前后MEMS陀螺仪原始信号见图9、图10，可以看出，温度补偿后，MEMS陀螺仪的输出大部分趋近于0附近，整体比较平稳，MEMS陀螺仪温度误差明显减小，精确度提高，说明一阶马氏链温度补偿模型补偿效果较好。

3.2 多MEMS监测系统与常规仪器沉降值对比

猴子岩面板堆石坝1 775 m高程（0+162.8断面）采用多MEMS监测系统与水管式沉降仪两套设备进行坝体沉降监测。多MEMS监测系统是分布式监测，采样频率为100 Hz，可以近似认为该系统测得的点是连续的。水管式沉降仪只有6个监测点（1 775 m高程（0+162.8断面）第7个测点已坏，故该断面为6个测点），因此两组监测数据可以在这6个点上进行对比。由图11可知，多MEMS监测系统监测1 775 m高程（0+162.8断面）沉降曲线与水管式沉降仪监测曲线趋势一致。同时，水管式沉降仪是点式监测，具有局限性，不能完全展现整个坝段沉降状况，不能测出该断面的最大沉降点。多MEMS监测系统分布式监测可以充分展现出分布式监测的优势。

4 结 语

（1）针对MEMS陀螺仪设计了温度特性的试验方案，通过试验得出了MEMS陀螺仪的温度漂移规律，即温度越高，MEMS陀螺仪产生的零偏波动幅度越大。

（2）基于回归理论的最小二乘法多项式拟合模型，确定多项式补偿模型为4阶，结合MEMS陀螺仪温度漂移规律，建立了多项式温度漂移补偿模型，该方法能有效提高零偏稳定性，精确度满足一般的监测需求。马氏链模型通过建立概率模型来进行温度补偿，其补偿效果优于多项式拟合模型的，精确度更高。

（3）马氏链温度补偿模型在猴子岩面板堆石坝的应用表明，一阶马氏链温度补偿模型明显降低了温度漂移误差，能够有效提高MEMS陀螺仪的精确度，能够更好地反映面板堆石坝变形的真实情况，具有一定工程实用性。

参考文献：

[1] 杨泽艳，周建平，蒋国澄.中国混凝土面板堆石坝的发展[J].水力发电，2011，37（2）：22-27.

[2] 蔡德所.分布式光纤温度传感系统和光纤陀螺技术在大坝工程中的应用研究[M].桂林：广西师范大学出版社，2013：35.

[3] 陈光富，蔡德所，李玮岚.光纤传感技术在大坝安全监测中的应用探讨[J].水电能源科学，2011，29（7）：70-72，168.

[4] 黎佛林，蔡德所，秦鹏.水布垭水电站面板挠度监测方法比较[J].水力发电，2013，39（1）：86-88，92.

[5] 孙役，李昌彩，王云清.高混凝土面板堆石坝设计与施工理念[J].水力发电，2007，33（8）：5-9，18.

[6] 王赏，蔡德所，王一立，等.磁惯导系统在大坝变形监测中的应用研究[J].人民长江，2017，48（3）：97-101.

[7] 许宜申，王寿荣，吉训生，等.微机械振动陀螺仪正交误差分析[J].北京：仪器仪表学报，2006， 27（增刊1）：105-107.

[8] 代刚. MEMS-IMU误差分析补偿与实验研究[D].北京：清华大学，2011：48.

[9] 李锷，颜樹华，周春雷.光纤陀螺温度漂移建模与补偿[J].半导体光电，2009，30（4）：45-48.

[10] 钱峰.基于受控马氏链的干涉型光纤陀螺温度漂移模型[J].光电子激光，2003，14（7）：705-708.

[11] 王连球.马氏链平稳分布存在与唯一性的简洁证明与计算[J].数学理论与应用，2007（1）：40-43.

[12] 孙飞跃，杨卫国.关于非齐次马氏链的一个定理[J].纯粹数学与应用数学，2015，31（6）：620-627.

[13] 金少华，刘姣，王东，等.关于非齐次树上m重连续状态马氏链的一个强大数定律[J].数学的实践与认识，2017，47（21）：277-283.

[14] 谈振藩，张勤拓.MEMS陀螺误差辨识与补偿[J].传感器与微系统，2010，29（3）：39-41.

[15] 徐朝勇，谭恺炎，胡升伟，等.猴子岩面板堆石坝安全监测技术[J].大坝与安全，2017（1）：29-33.

【责任编辑 吕艳梅】