和积原理——两正数和与积的关系
2020-10-20邓志雄
邓志雄
道理是事物具有的规律,是用以判断是非的规则和理由,也是据以处理事情的办法和打算。道理有大有小,小道理要服从于大道理。原理就是大道理。原理是具有普遍意义的道理,是可以作为其他规律的基础的规律。
通过多年的琢磨,笔者逐渐体悟出两正数的和C=X+Y与积S=XY中包含的一个重要原理,并尝试用这个原理分析解释了一些经济和社会问题,得到了一系列新的认识。特请《产权导刊》开辟专栏与读者分享,希望感兴趣的同志结合实践做出更多拓展。
1 加法中的“和为常数现象”及其特点
小学一年级一开始,数学课就学10以内的加法。几加几等于10,是十进制算法中必须掌握好的重要学习内容和运算方法。
1+9=10,2+8=10,3+7=10,4+6=10,还有,5+5=10。
这5个等式,右边的和都是10,左边两个相加的数则是此消彼长并互补为10的:1和9,2和8,3和7,4和6,5和5。一方面此消彼长,一方面和为定数,这两个特点将给我们带来很多有趣的讨论。
放开了去想,100以内的数,也有这样的特点吗?
有的!
1和99,2和98,3和97,......,10和90,......,20和80,30和70,......,40和60,......48和52,49和51,50和50,一共50组数,都是两加数此消彼长并互补为100的。
再放开去想,在1000以内,10000以内......直到更大范围内,我们都能找到这种“两个正数之和为常数”的现象。用代数来表达,就是“X>0,Y>0,且X+Y=C,C为常数”。
值得重点说明的是:和为常数的两个正数一定是围绕常数此消彼长的,而此消彼长的两个正数必然互补形成一个常数。这是因为,在等式X+Y=C中,当C是常量时,X扩大Y就得等量缩小,X缩小Y就得等量扩大,即:(X+⊿)+(Y-⊿)=X+Y=C,所以和为定值的两正数的变化总是围绕着这个定值此消彼长的。反过来看,也有此消彼长的两个正数的和一定为定值。这是因为系统中只有此消彼长的两个数,若一个减小与另一个的增大等值,自然导致二者之和不变,即:(X-⊿)+(Y+⊿)=X+Y=C。
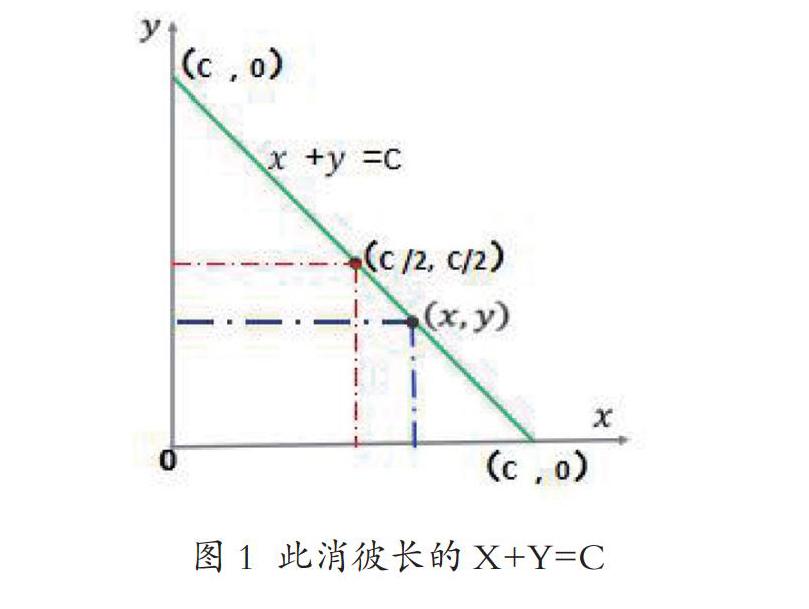
这一特点在直角坐标系中可以看得更清楚。如图1所示,X+Y=C是经过(C,0)、(0,C)两点的直线,(X,Y)是直线上一个动点。当动点沿直线运动时,始终有X+Y=C和X与Y此消彼长的约束关联。因C不变,任何X之长必导致Y的等量之消,反之,任何X之消必要求Y的等量之长。更清楚些看,令C=1,则X和Y就是互补为1的两个小数,它们之间当然是此消彼长的关系。
2 和为常数的两个正数的乘积比较
将10以内和为10的5组数彼此相乘,我们发现:
1×9=9,2×8=16,3×7=21,4×6=24,5×5=25。
认真观察思考,读者会有三个发现:两乘数的差距越大,其积就越小。两乘数差距越小,其积就越大。两乘数相等时,其积最大。
显然,不难验证,在100以内、1000以内、10000以内,情况也是这样。
更开放些,可以想象,在无限大范围内,当“两个正数之和为常数时,其乘积将在两数差距增大时缩小,在两数差缩距缩小时增大,并在两数差为0即两数相等时取得最大”。
当然,这需要加以数学证明。
3 和积原理的代数表达与证明
上述思想用代数语言表达就是:“若X>0,Y>0,且X+Y=C,C为常数,则S=XY将在X与Y的差距扩大时趋于缩小,在X与Y的差距缩小时趋于增大,并在X与Y的差距为0即X=Y时取得最大值”。
这里,两数差距指两数差的绝对值。其证明如下:
由于X+Y=C,C为常数,
故有:
S=XY
=X(C﹣X)
=CX﹣X?
=﹣(X﹣C/2)? + C2/4
由于﹣(X﹣C/2)?≤0,因此,当(X﹣C/2)增大时,S将趋于缩小;当(X﹣C/2)缩小时,S将趋于增大;当(X﹣C/2)=0即X=Y=C/2时,S将取得最大值:SM= C2/4。
而当X>C/2时,|X-Y|=2X-C,(X-C/2)增大即X增大,X与Y的差距|X-Y|=2X-C将随之增大;
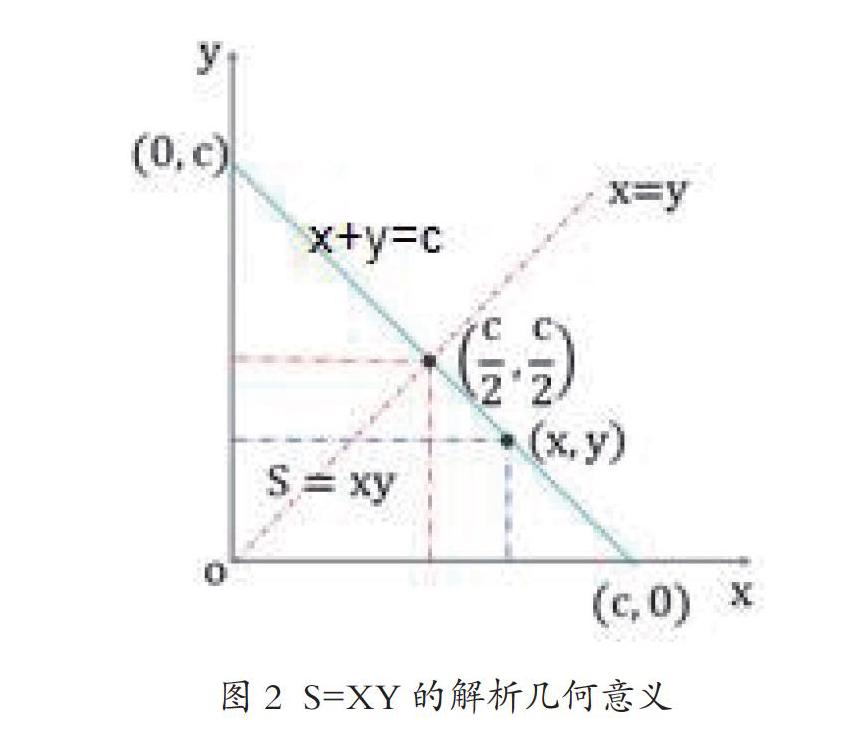
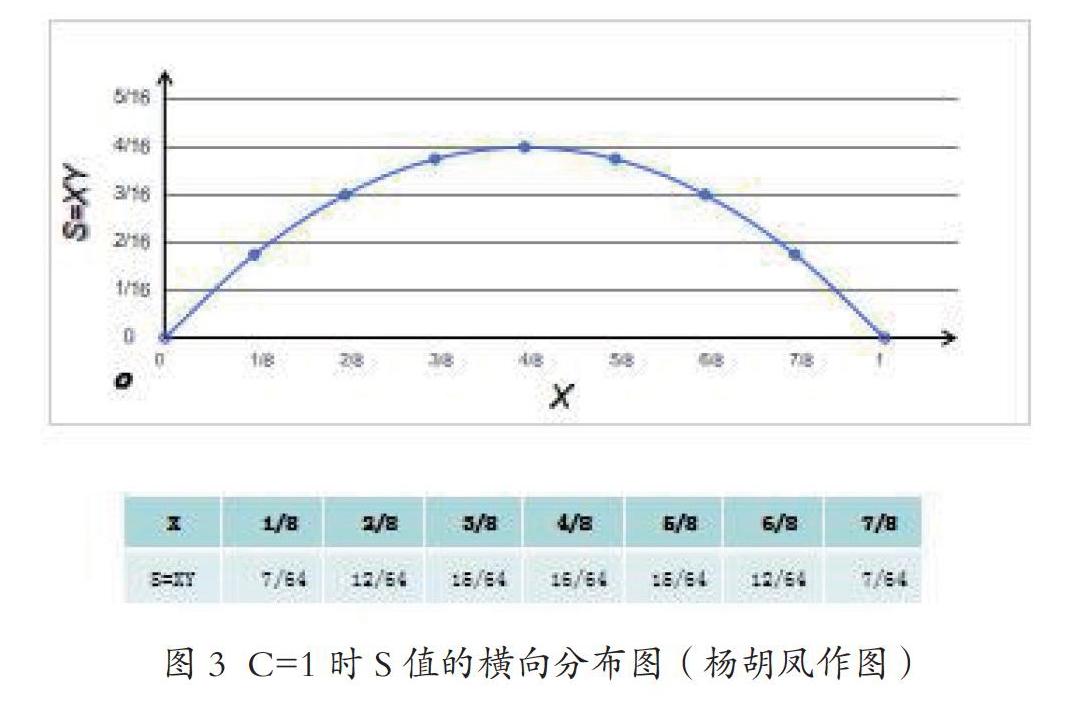
当X 当(X-C/2)=0时,X=Y=C/2,X与Y的差距|X-Y|=0。 于是得证! 这个定理揭示了两个正数X与Y的“和”C=X+Y与“积”S=XY变动趋势的关联关系,利用这条定理中相关因素间的运动规律和辩证关系,我们可以解释不少经济社会现象,即这条定理是一条能管大用的科学原理,因此,我们将这条数学定理命名为“和积原理”。 4 和积原理的几何意义 恩格斯说,“笛卡尔的变数是数学中的转折点,从此,运动和辩证法进入了数学。”如图2所示,把S=XY放到笛卡尔直角坐标系中去表达,我们可以更清晰的看到,点(X,Y)沿着直线X+Y=C运动时,表现为长方形面积的S=XY变化的趋势和极值情况。 图2中,X、Y都处在第一象限,表示X>0,Y>0;满足X+Y=C的点集合在连接但不包括(C,0)、(0,C)两点的线段上,它们共同构成了S=XY极值原理的边界条件。点(X,Y)是边界线段上的一个动点,其横坐标是X,纵坐标是Y,这个点沿着边界线段运动时,分别以其横坐标X和纵坐标Y为长和宽的矩形的面积S=XY随之发生变化。點(C/2,C/2)是边界线段的中点,连接这个中点和坐标系原点的直线的方程是X=Y,由这个中点为右上角构成的矩形是代表SM的正方形。 S=XY的解析几何意义主要是点(X,Y)的运动带来的以下几个特点: 1.当动点(X,Y)向着中点(C/2,C/2)运动时,无论是从(C,0)点往左上行,还是从(0,C)点往右下行,都会出现X与Y的差距不断减小,二者大小逐渐趋向均衡,矩形S随之趋近于正方形,其面积S不断扩大; 2.当点(X,Y)与中点(C/2,C/2)重合时,X=Y=C/2,X与Y差距为0,矩形S变成正方形,矩形面积S=XY达到最大值:SM= C2/4。 3.当动点(X,Y)从中点(C/2,C/2)沿着边界线向(C,0)点运动时,虽然X逐渐增大,但同时Y不断减小,X与Y的差距越来越大,导致S=XY逐渐变小,当动点(X,Y)趋近于点(C,0)时,S=XY便趋近与0,二维的矩形趋近消退成一条没有面积的一维直线(X轴)。 当动点(X,Y)从中点(C/2,C/2)沿着边界线向(0,C)点运动时,虽然Y逐渐增大,但同时X不断减小,Y与X的差距也越来越大,也会导致S=XY逐渐变小,当动点(X,Y)趋近于点(0,C)时,S=XY也趋近于0,二维的矩形亦趋近消退为一条没有面积的一维直线(Y轴)。 上述解析图像十分明晰地告诉我们,在X>0、Y>0,X+Y=C的前提下,X、Y要相向而行,S=XY才能在X与Y的均衡增长中不断实现增长;X与Y要取得相等,S才能获得最大;一旦X和Y背道而驰,S就会随之减小。和积原理的这些重要思想和科学结论,我们将在讨论资源利用最大化、复合资本市场建设、混合所有制发展、病毒疫情防控和企业管理等问题时反复加以利用。 5 S值的单因素分布情况 将上述讨论中S值大小的变化沿坐标系横轴展开,我们可以作出C为定值时S值的横向分布图。 一般而言,二次函数S=aX2+bX+C的图像是一条抛物线。二次项系数a决定抛物线的开口方向,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。抛物线对称轴为直线x=-b/2a。对称轴与抛物线唯一的交点为抛物线的顶点P,其坐标为P(-b/2a,(4ac-b2)/4a)。 按照上述“3”中的分析,S相对于X的函数式为S=﹣X2+CX 。按照上述知识,这条抛物线开口向下,顶点最高;对称轴为X=C/2;顶点坐标为P(C/2,C2/4),即X=Y=C/2时,SM= C2/4。 令C=1后作图,所得图3就是S值的横向分布图。这是一条以(1/2, 1/4)为顶点的开口向下的抛物线。在X值从0(不含0)向1/2逐步增大的时候,S的值随之逐步增大,但增速逐渐降低。当X值等于1/2时,S的值达到最大值 1/4 。当X值大于1/2后继续向1增大时,S的值逐步减小,减速逐步加快。当X趋近于1,S就趋近于0。 图4给出了C=1/2、C=1、C=2、C=3时S值的横向分布组图。由图可见,随着C值的增大,S的极大值有更快的升高。其中原因在于SM= C2/4中,当C发生增长时,SM会发生C2倍变化,其间蕴含着一种倍积的力量。 图5是C=10时S值的横向分布情况。此时,S值的曲线已经是一个高挑漂亮的抛物线了。可以想象,当C取更大数值时,S的曲线将变得更高更尖。 基于X、Y的对称性,可照此作出S沿Y轴展开的纵向分布图。事实上,将图2的X轴反时针旋转900到Y轴位置就得到S的纵向分布图。而在旋转过程中产生的切割体就是S=XY的立体模型。 S值单因素分布图的一个重要特点是,除了抛物线的顶点之外,相对于每一个S值,都有两个X值与之对应。两个X值对应同一个S值,在经济问题中就出现政策取舍问题。这一特点将在讨论拉弗曲线时再作深入分析。 6 两数之积S的极大值SM 从第三节的分析中我们得知,两数之积S的极大值SM由两数之和C来决定:SM= C2/4。若在一定的时段内,X与Y两数之和C不变,这个阶段中两数之积S的极值就不会增大或缩小。进入一个新的阶段后,当C发生变化,S也就将随之发生变化。由此产生做大蛋糕C=X+Y以求得S新的发展空间问题。如图6所示,当直线X+Y=C向内外平行移动时,其中点(C/2,C/2)将沿着直线X=Y运动。因此,不同的C值将共同给出一组不同位置上X+Y=C的平行线。显然,要分阶段做大S的极值,就得创造条件,打破常规,争取隔一段时间就将边界线平行向外推进一段,分阶段做大C值这个蛋糕。当然,工作中更要尽力防范系统风险,始终保持X与Y的均衡,严防C的向内缩减带来的系统性衰退。有关这方面的深入讨论,将在分析帕累托改进与帕累托最优问题时展开。 7 和与积的跨越发展边界线 值得指出的是,由于小数乘法自身的规律性,在S的增长过程中存在着一条关键性的跨越发展边界线。结合图4和图7分析可知: 在0 在C>1阶段,C2>C,指数函数的升维效应得以发挥作用,两数积S会随着两数和的增长出现更加快速的增长。 这就表明,C=1是S发展提升中的一条跨越发展边界线。在此之前,SM的极值空间非常有限,在此之后,S的极值空间迅速拓展。马泰效应等强者恒强的经济社会现象可以由此得到解释。先发国家占据科技与金融等C>1的高端实现持续发展,多数后发国家则仍然处在人才与资本等C<1的低端未能有效突破,原因就在于此。前者倍尝XY>X+Y好处,后者吃尽XY
