在数学教学中渗透“非线性”的教学理念

谢倩妃

【摘要】如何让学生由学会变为会学，成了数学教学的关键。而林少杰老师的“非线性”教学理念、操作原则，在教会学生思考方面给我们提供了一套行之有效的方法。

【关键词】“非线性”教学理念;应用;思维能力

林少杰老师的“非线性”教学理念具有开放性、自组织性、不可逆性和循环性等特征。它最大的特点是：主张整合教学内容，淡化形式、注重实质，注重分层指导，充分重视课堂活动和多种学习方式的组合运用，充分释放学生的潜能，培养学生的探索创新精神和自学能力。

学习了林少杰老师的“非线性”教学理念我对课堂教学结构进行了大胆的改革，主要采取以下几种方法：

一、课前预习（独自领悟，合作发潜）

在学习材料以整体3/4局部3/4整体的方式呈现的“非线性”状态下，学生的感悟才会形成，才会有良好的学习效益。数学教学中，教师不仅要教会学生对数学语言的翻译，更重要的是教导学生怎样读数学。因此，我在课前安排了“问题情景”，采取实验操作，问题探索，以引起学生解决问题的动机，驱使他们在好奇心的诱发下进入探索境界。

通过提出问题，让学生读书时会抓住要点，学生的思维带有明确的目标，从而大大的节约了课堂讲授时间，增加了学生思考和练习的时间，充分提高了课堂效率。

预习在课堂学习中把握住重点、难点和关键，更重要的是这种自学的过程锻炼了学生探索数学问题的能力，在探索中对数学知识的内化得到了加强，关注教学内容的“生成”。

二、新旧融合（先试后学，先学后教）

过去上课前5-10分钟主要用于复习检查和纠正作业，人为地设置了新旧知识的界限，既耽误时间又不能激发学生的积极性，也不利于提高学习能力。现在在传授知识时，我往往采取问题探索，尝试练习等多种形式把新旧知识融合在一起，让学生在不知不觉中完成由旧到新的思维过程。

例如我在讲九年级上册第二十四章《圆》中圆周角的最后一课（86页例题2）时，事先设计了一组前后联系密切的练习题。

1.已知：在圆0中，直径AB=10cm，.AC=6cm.求BC.

2.已知：在圆0中，CD平分圆周角∠ACB，交圆0于点D，求证：？AD=BD。

3.已知：在△ADB中，∠D=90，AD=BD.AB=10cm，求AD、BD的长。

出示例题：已知：在圆0中，直径AB=10cm，弦AC为6cm，∠ACB的平分线交圆0于D，求BC、AD、BD的长。

通过前三个练习的解答既可加深对前节定理的理解与应用，而且综合起来正好组成本节例题，这样对看似复杂的例题也就迎刃而解了。教师讲授的时间累计不超过15分钟，把大量时间留给学生作思考，内省、练习和展示，学生自主学习的时间多了，所有习题几乎全在课内完成，课堂上学会了，教师不用布置课外作业。利用“先试后学，先学后教”这种方式，既关注教学事件的“歧化”又关注教学关系的“循环”。虽然教师课前下的工夫多，但有助于学生对所学知识的巩固和加深理解，难易适度。最重要的是，学生动手动脑的能力能得到充分锻炼，并培养学生的思维能力。

三、鼓励尝试（课内批改，个别提点）

几何题往往一题有多种思路，在讲解时由于害怕学生不会而耽误时间，总是加以提示，学生跟着老师的思维方向去做题，这不仅限制了学生思维能力的发展，长此下去，也使他们丧失了向难题挑战的勇气。学习了“非线性”教学理念后，不但改变了我的教学观念，也大大激发了学生的思维，课堂由过去的“一言堂”变成了“多言堂”。

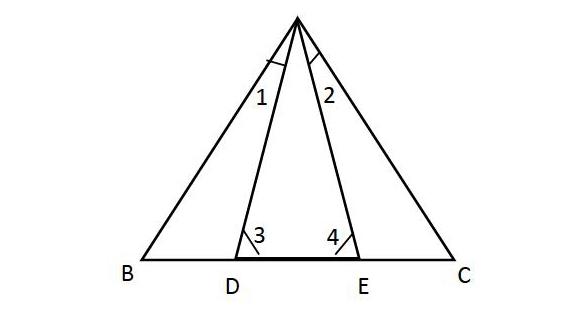
例如习题：如图点D、E在BC上，∠B=∠C，∠l=∠2.求证：AD=AE。

同学们经过独自思考，各抒已见，有的利用了（ASA）定理证全等，有的利用等角对等边，有的证明两次三角形全等，有的说要过A点作BC的垂线，有的说要作BC边上的中线，有的说要作∠BAC的角平分线（利用等腰三角形三线合一）等等。我让他们按自己的想法去写，做好后就举手，让我批改，然后让他们到黑板上写出不同的证明过程。通过对他们的想法进行交流，同学们既可以取长补短，找出最简捷的方法，又可以开拓思维，使教学过程发挥最大的效益，关注教学过程的“交流”，通過课内批改，个别提点，注重分层指导，不仅能更好的把每个学生的错误想法及时纠正，而且能更好地启发学生的观察、分析能力，学生的思维能力也就得到了提高。

四、以题复习（精设主干，精选训练）

以前单元复习总是把知识点一个一个个罗列出来，当把整章书的概念、定理复述一遍后，一堂复习课就差不多结束了，这样的复习既浪费了时间又收不到效果。学习了“非线性”教学理念后，认识到知识的掌握只有在运用中才能掌握。现在改变了策略，精选例题训练，学生在做完题目后就已达到复习的作用，还充分训练了学生的思维。

例如在讲八年级下册第十九章《四边形》复习课时，我出了这样一道题让学生做：

如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C'处，折痕DE交BC于点E，连结C'E。

（1）求证：四边形CDC'E是菱形;

（2）若BC=CD+AD，试判断四边形ABED的形状，并加以证明。

学生已经学习了整章书的内容，包括平行四边形、矩形、菱形、正方形、梯形、等腰梯形等。这章书有很多性质定理和判定定理，通过做这道题目，学生必需要清楚梯形的性质，还有菱形的判定，然后用条件证明四边CDC'E是菱形。在这个过程中，学生又要想平行四边形的性质和菱形的判定，又要与矩形、正方形的判定区别开来，老师抓住知识的主干线进行引导和精讲评。其实，完成这道题就已经把这章书的主要知识都复习遍了。这样，通过教师的引导、点拨，让学生自己去发现、归纳的过程，既有益于学生思维的启动和发展，还可以教会学生如何学习数学。

参考文献：

[1]林少杰.数学教学内容的非线性结构[J].教育导刊，2002（08）.

[2]林少杰.数学技能训练系统的构建及课内技能训练策略[J].中学数学研究，2002？（07）.

[3]施良方.教学理论：课堂教学的原理、策略与研究[M].上海：华东师范大学出版社，2005.

[4]丁石孙，张祖费.数学与教育[M].长沙：湖南教育出版社，1989.