慢条斯理说辅助圆

赵一霖

[摘  要] 近几年江苏高考数学中很多题目看似表面上与圆毫无关系，经过我们细致分析，探索本质引入辅助圆可以使问题极大的简化. 这些题目得分率较低，入手较为困难主要是学生对于其本质没有搞清楚. 文章结合课堂实例，归纳总结引入辅助圆的几种类型.

[关键词] 辅助圆;圆;阿波罗尼斯圆;定值

圆是平面解析几何中最优美的图形之一. 它表示平面内到定点的距离等于定长的点的集合，具有对称性等性质.有很多题目从表面上看与圆毫无关系，但经过分析结合圆的特征，我们就会发现有的题目其实和圆有很大的关系，这时我们就可以引入辅助圆，使问题得到极大的简化.本文结合具体课堂实例，归纳总结引入辅助圆的几类题目.

特征一：到定点的距离等于定长的点的集合

例1：如果圆（x-a）2+（y-a）2=4上总存在两个点到原点的距离为1，则实数a的取值范围是__________.

解答：由题意可得. 圆（x-a）2+（y-a）2=4和圆x2+y2=1相交，

两圆圆心距d=■=■a，由两圆相交可得1<■a<3，所以a的取值范围是-■■，-■∪■，■■.

本质思考：到原点的距离为1，就应该考虑圆的定义：到定点的距离等于定长的点的集合，从而引入辅助圆.同理，到定直线的距离为定值，到定点距离为定值的直线集合都应考虑引入辅助圆求解.

例如：①已知点A与点P（2，0）的距离为2，且到y轴的距离为1，则点A的坐标为__________.

②已知到点P（2，0）的距离为2，且到点Q（-4，0）的距离为4的直线有________条.

①就可以看做直线与圆相交问题，②可转化为两圆公切线问题.

特征二：到两定点的向量积等于定值

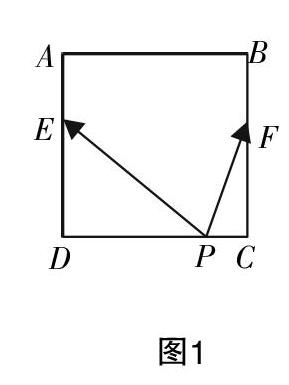
例2：如图1，正方形ABCD的边长为6，点E，F分别在边AD，BC上， 且DE=2AE，CF=2BF. 如果对于常数λ，在正方形ABCD的四条边上，有且只有6个不同的点P使得■·■=λ成立，那么λ的取值范围是__________？摇.

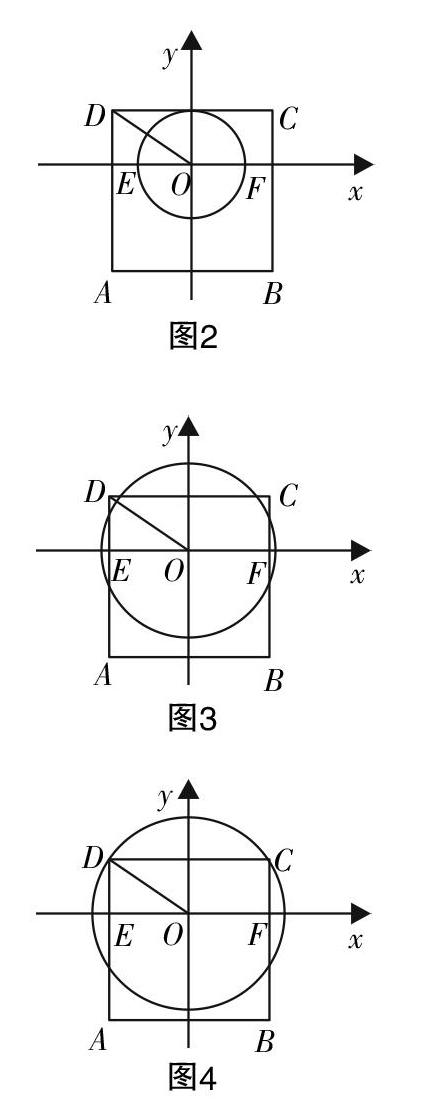
解析：以EF的中点为坐标原点建立直角坐标系可以容易得出点P所在的轨迹为圆x2+y2=λ+9.

如图可知若是圆P与正方形有六个交点，其半径必须介于图一与图三之间，即3<■<■，所以0<λ<4.

本質思考：此题采用了几何意义，关键在于点P的轨迹是圆，由此问题转化为直线与圆的位置关系.我们得出一个结论：

在平面上给定相异两点A，B，AB=2a，设P点在同一平面上，且满足■·■=λ（λ>-a2），点的轨迹是圆.

我们再看下面一题

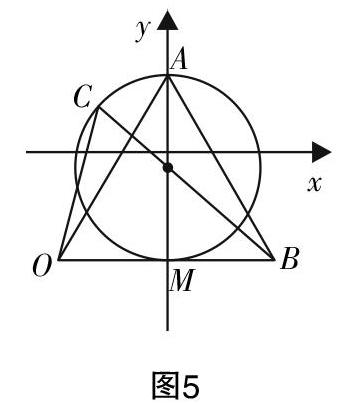
例3：已知a=b=a·b=2，（c-a）·c-■=0，求b-c的取值范围.

解：由a=b=a·b=2可知，a与b的夹角为60°，故a，b与a-b构成一个边长为2的等边三角形OAB，其中■=a，■=b. 由（c-a）·c-■=0可知到点A、OB的中点M的向量积为0，故c的轨迹是以点A、OB的中点M为直径的圆，此时引入辅助圆记为⊙C，半径为r=■. BC=b-c，所以b-c∈■，■.

■特征三：到两定点的比为定值（阿氏圆）

例4：已知AB=2，AC=■BC，则△ABC面积的最大值是__________.

解：以直线AB为x轴，线段AB的中垂线为y轴，建立平面直角坐标系，则A（-1，0），B（1，0）. 设点C（x，y），？摇？摇由题意得：AC2=2BC2，即（x-3）2+y2=8. 所以点C在以（3，0）为圆心，2■为半径的圆上运动，所以点C到直线AB的距离的最大值为半径2■，所以S△ABC≤■×2×2■=2■.

本质思考：在平面上给定相异两点A，B，设P点在同一平面上，且满足■=λ，当λ>0且λ≠1时，P点的轨迹是个圆，称之为阿波罗尼斯圆，简称“阿氏圆”.

（λ=1时，P点的轨迹是线段AB的垂直平分线）

特征四：到两定点的角度为定值表示一段圆弧

例5：设双曲线x2-■=1的左、右焦点分别为F1，F2，P为直线x=4上的动点，若∠F1PF2=θ，则θ的最大值为_________.

解：设x2-■=1的左、右焦点分别为F1（-2，0），P为直线x=4上的动点，若∠F1PF2=θ，则F2（2，0）当过这三点F1，F2，P的圆与直线x=4相切时θ最大，最大值为30°.

本质思考：平面A，B为两个定点，设P在同一平面内，若∠APB=θ（0<θ<π）表示一段圆弧，当这个圆与x=4相切时θ取得最值.

特征五：圆外一点引的切线长相等

例6：x，y为正数，且x+2y=1，求■+■+■的最小值.

解：令■=a，■=b，本题可转化为已知■+■=1，求a+b+■的最小值问题. ■+■=1可看作恒过（1，2）点的直线，a+b+■可看作求OA+OB+AB的最小值问题. 我们可以引入一个辅助圆（x-c）2+（y-c）2=c2，且该圆过点（1，2），则c=5使得直线AB与圆相切，因为切线长相等，所以最小值为OA+OB+AB=OF+OE=2c=10.

通过以上例子我们知道，如果满足圆的如上几个特征，就可以考虑引入辅助圆，结合辅助圆的相关性质简单明了快速求解原问题.