深剖空间距离，例析问题解法

汪艳

[摘  要] 空间距离问题是立体几何中的典型问题之一，能够全面考查学生对空间距离的理解，以及空间几何观.  空间距离问题的类型较多，垂线段法、等体积法和空间向量法是最为常用的方法，同时其方法思想具有一定的代表性，文章对空间距离问题加以探讨，并结合实例探究三种方法.

[关键词] 空间距离;垂线段;等体积法;向量法;思想

问题综述

空间距离是刻画空间中的点、线、面相对位置数量关系的一个重要的量，也是立体几何部分重要的研究问题. 纵观历年高考，主要以求解点到点、点到线、点到面、线到线、线到面的距离为核心，空间距离的求解一般将其转化为计算线段长，问题难点主要集中在以下几个方面：一是如何处理图形特点与相关概念的关联，即理解问题条件;二是如何对空间元素的距离进行转化，尤其是线面距离、异面直线距离;三是空间距离的求解方法较多，如何根据方法步骤来构建转化思路. 下面将对点到平面、线到平面的距离以及异面直线距离的解法举例探究.

方法概述

求解空间距离的方法有很多，对于点到平面、线到平面的距离的解法可以归为以下四种：①垂线段法，即直接作点或直线到平面的垂线段，问题转化为常规的线段长问题;②等体积法，根据立体几何中高的定义可知，高为顶点或上平面到底面的距离，而对于同一几何体，可以从不同的视角来构建体积模型;③向量法，该方法是建立在空间坐标系上的一种特殊方法，充分利用了向量射影长的距离内涵. 而对于异面直线距离问题，可以将其转化为点到平面或直线到平面之间的距离，在实际求解时需要结合具体的问题特点来合理选定方法，确保过程简捷，思路清晰，作答准确.

举例探究

点到平面、线到平面的距离是其中的难点问题，其方法在处理空间距离问题中具有一定的代表性，下面举例探究垂线段法、等体积法和向量法的解析技巧和解题思路的构建.

解法一：垂线段法

垂线段法即是从定义出发直接求距离的方法，相对于后续两种方法较为直接，从空间距离的问题本质来看，实则就是求空间元素之间的垂线段，因此若能直接作出垂线段，则可以采用此方法. 垂线段的作法有多种方式：①若过该点的直线同时垂直于平面内的两条直线，则该直线垂直于目标平面，就可以在该直线上截取垂线段;②也可以过直线作目标平面的垂直平面，可得两平面的交线，将其转化为两平行线之间的距离，显然很容易获得垂线段.

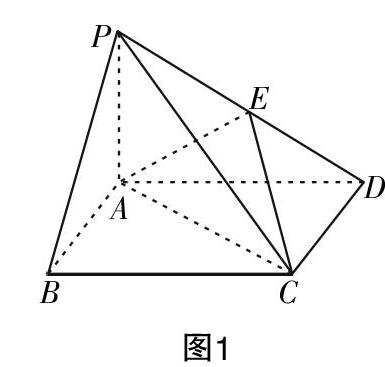
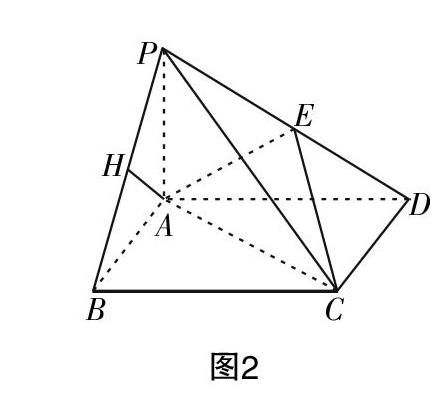
例1：如图1所示，已知ABCD为矩形，PA⊥平面ABCD，点E为线段PD的中点，试回答下列问题.

（1）证明：PB∥平面AEC;

（2）若AP长为1，AD长为■，且三棱锥P-ABD的体积为■，求点A到平面PBC的距离.

分析：第（2）问求点A到平面PBC的距离，分析可知只需要过点A作平面PBC的垂线段即可. 基本思路是确定垂直于平面PBC且过点A的平面，则过点A作两平面交线的垂线，则垂足到点A的距离就为所求的垂线段.

解：已知AP=1，AD=■，三棱锥P-ABD的体积可以表示为V=■PA·AB·AD，代入可得AB=■，根据勾股定理可得PB=■=■. 由于PA⊥平面ABCD，则PA⊥AD. 又知四边形ABCD为矩形，则AB⊥AD. 综上可知AD⊥平面PAB，又知AD∥BC，则BC⊥平面PAB. 又知BC平面PBC，故平面PAB⊥平面PBC，过点A作PB的垂线，垂足为点H，如图1所示，可证AH⊥平面PBC，则AH长就为点A到平面PBC的距离. 将AH放在△PAB中，其中∠PAB=90°，由等面积可知PA·AB=PB·AH，则AH=■=■，即点A到平面PBC的距离为■.

解法二：等体积法

等体积法同样适用于空间距离求解，该方法与等面积法的构建思路是一致的，即从不同的视角来构建几何体的体积，利用体积相等来求解其中的线段长. 等体积法一般适用于规则几何体，且高为所求距离的值. 解析时首先转化视角确定几何体的底面，然后结合线段长来构建代数方程.

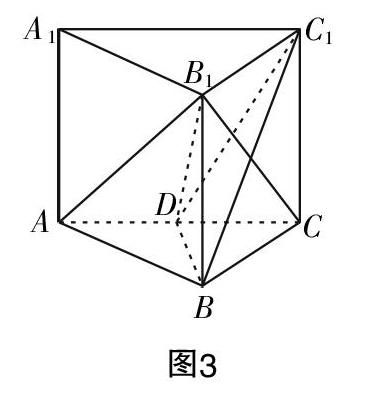
例2：如图3所示，正三棱柱ABC-A■B1C1的底面边长为8，对角线B1C的长为10，点D为AC的中点，试回答下列问题.

（1）求点B1到直线AC的距离;

（2）求直线AB1到平面C■BD的距离.

分析：（1）问求点到直线距离，图中所示几何体为特殊的正三棱柱，点D为AC的中点，有BD⊥AC，则DB1就为所求垂线段，后续将其放在三角形求解即可.

（2）设直线BC1与B1C交于点E，分析可知AB1∥DE，则AB1∥平面BDC1，所以AB1到平面BDC1的距离就等于点A到平面BDC1的距离，同时就等于点C到平面BDC1的距离，后续就可以在三棱锥C-BDC1中利用等体积法求解.

解析：（1）在正三棱柱ABC-A1B1C1中，因為点D为AC的中点，所以有BD⊥AC，连接B1D，由三垂线定理可知B1D⊥AC，则B1D就为所求距离. 在Rt△BB1D中，已知BB1=6，BD=4■，由勾股定理可得B1D=■=2■.

（2）设BC1与B1C交于点E，由于AB1∥DE，则AB1∥平面BDC1，所以A到平面BDC1的距离等于点C到平面BDC1的距离. 对于三棱锥C-BDC1，可将其视为以点C为顶点、平面BDC1为底面的三棱锥，则V■=■hS■（h表示点C到底面BDC1的距离），同时可将其视为以点C1为顶点，以平面BDC为底面的三棱锥，则V■=■·CC1·S■. 由等体积可知hS■=CC1·S■，则h=■，即直线AB1到平面C1BD的距离为■.

解法三：空间向量法

向量法是求解空间几何问题的常用方法，该方法具有简洁直观的优点. 求解时可以按照空间向量的分析步骤进行，即首先建立空间直角坐标系，然后求出关键点的空间坐标，推导其中的线段向量，最后结合公式d=■ （其中点P为平面α内的一点，n为平面α的法向量）即可确定点A到平面α的距离.

例3：如图4所示，在多面体ABCDE中，平面ABD⊥平面ABC，已知AB⊥AC，AE⊥BD，DE∥AC，DE=■AC，且AD和BD的长均为1，试回答下列问题.

（1）求AB的长;

（2）若2≤AC≤4，求点E到平面BCD距离的最大值.

分析：（1）略;（2）在多面体ABCDE中，无法直接确定点E到平面BCD的垂线段，此时可以建立空间直角坐标系，利用空间向量来求点到平面的距离.

解：由于AD=BD，则△ABD为等腰三角形，取BD的中点为O，平面ABD⊥平面ABC，OD⊥平面ABC，过点O作AC的平行线，与BC交于点Y. 以点O为空间坐标原点，分别以OB，OY，OD为x，y，z轴，建立空间直角坐标系O-xyz，如图5所示.

记AC=2a，则1≤a≤2，则A-■，0，0，B■，0，0， C-■，2a，0，D0，0，■，E0，-a，■，■=（-■，2a，0），■=-■，0，■. 可推算出平面BCD的法向量n=■，■，■. 又知■=（0，-a，0），则点E到平面BCD的距离可以表示为d=■=■. 其中1≤a≤2，分析可知当a=2时，d可取得最大值■，即点E到平面BCD距离的最大值为■.

解后思考

1. 回归教材基础，系统梳理方法

空间距离是高中数学的重点问题，也是数学教材探讨的重点内容. 对该问题的探究剖析需要回归教材，把握教材的基础知识，包括线面垂直、面面垂直、线面平行的性质定理和判定定理，深刻理解空间距离中垂线段构建的原理及思路. 空间距离问题的类型较为多样，方法也存在差异，学习时需要对其中的典型方法进行系统梳理，可以采用对比归纳的方式，对方法的原理、特点、优劣、适用题型和构建思路进行整理，从而形成自我的解题策略. 例如上述呈现的三种方法适用题型有如下特点，其中垂线段法适用于容易作出垂线段的问题，等体积法适用于几何结构规则且垂线段为高的问题，空间向量法具有一般性. 对方法的梳理实则就是对问题特点的剖析，同时也是考题探究的必要环节，有助于提升学生的解题能力.

2. 探究方法思想，重视方法反思

空间距离问题属于三维问题，对于学生而言较为抽象，上述方法是通过降维或转化的方式来简化问题. 如垂線段法和空间向量法是将空间问题转化为平面问题，等体积法是将其转化为方程问题，其中隐含着重要的数学思想. 开展方法探究需要重视反思方法本质，关注方法的指导思想，尤其是降维思想和转化思想，这两种思想是求解空间距离问题的关键，也是空间距离问题思路构建的内在原理. 另外，在方法反思教学中应注意引导学生对问题进行多视角剖析，对于某些问题可以采用多种方法求解，在反思过程中有必要开展一题多解，使学生深刻认识方法联系，多视角理解方法思想的内涵，最大化激发学生的学习兴趣，拓展解题思维.