典题为例深探究,问题深析重思考
2020-10-20陈硕罡
陈硕罡
[摘 要] 圆锥曲线问题在高考中有着重要的地位,考题设置有两大层次:一是立足基础,考查曲线的基本内容;二是立足综合,考查综合能力. 近几年考题侧重考查学生的探究能力,出现了一些具有探究性的考题,文章以一道圆锥曲线探究题为例,开展问题探究,解后反思,提出相应的建议.
[关键词] 圆锥曲线;探究;定点;面积;最值;思考
圆锥曲线典型问题探究
高考考查圆锥曲线的内容较多,涉及基本定义、标准方程、知识关联、几何性质等,往往问题综合性较强,近几年的考题逐步侧重考查学生的探究能力,出现了一些探究性问题,下面对一道圆锥曲线存在性问题进行探究.
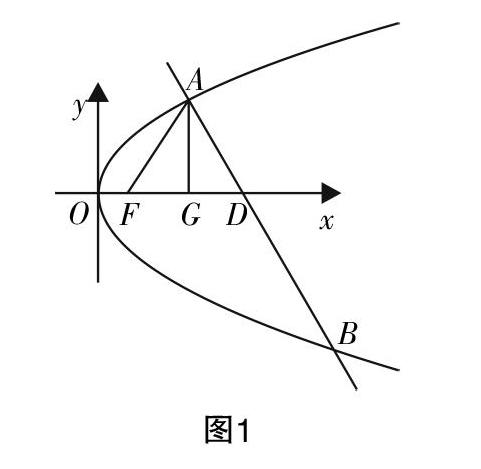
例题:已知抛物线C的解析式为y2=2px(p>0),点F是抛物线C的焦点,点A是曲线上异于原点的一点. 现过点A作直线l,与抛物线C的另一交点设为点B,与x轴正半轴的交点设为点D,且有FA=FD.当点A的横坐标为3时,△ADF为正三角形,试回答下列问题.
(1)求抛物线C的解析式.
(2)若直线l1与l平行,直线l1与抛物线C的交点有且只有一个,为点E.
①直线AE是否恒过一定点?若不存在,请说明理由;若存在,请求出该点的坐标.
②△ABE的面积是否存在最小值?若存在,请求出該最小值;若不存在,请说明理由.
思路点拨:本题目为高考常见的圆锥曲线压轴题,以抛物线为背景,考查解析式求解,探究直线过定点,探究三角形面积的最小值. 问题探究性极强,需要综合运用圆锥曲线的相关知识及探究方法. 例题设置了两大问,下面逐问探究.
(1)该问求解抛物线C的解析式,主要是求解析式中p的值,可设出交点F的坐标,利用条件FA=FD,根据抛物线的定义构建方程;
(2)该问分为两个小问,第①问探究直线AE是否经过定点,总体思路是设出点A和D的坐标,求得直线AB和l1的方程,然后联立直线l1与抛物线C的方程,从而可确定点E的坐标,得到直线AE的方程,通过对直线AE的方程简化即可论证是否经过定点.
第②问探究△ABE的面积是否存在最小值,属于曲线与几何的综合探究题,利用面积公式构建三角形的面积模型,将其转化为关于坐标参数的面积函数,结合函数性质或不等式性质论证是否存在面积最小值.
过程解析:(1)根据抛物线C的解析式可将焦点F的坐标表示为■,0,可设点D的坐标为(t,0)(t>0),则线段FD的中点坐标为■,0.已知FA=FD,根据抛物线的定义可得3+■=t-■,可解得t=3+p或t=-3(舍去),中点G与点A的横坐标相等,即■=3,可解得p=2,所以抛物线的解析式为y2=4x.
(2)①由(1)问可知焦点F(1,0),设点A(x■,y■)(x■·y■≠0),点D(x■,0)(x■>0).由于FA=FD,则x■-1=x■+1,解得x■=x■+2,则D(x■+2,0),由点A和D的坐标可得直线AB的斜率为k■=-■,又知k■=k■,则直线l■的方程可以表示为y= -■x+b,与抛物线的解析式联立可得y2+■y-■=0,由Δ=0,可得b=-■. 设点E的坐标为(x■,y■),则有x■=■,y■= -■. 当y■≠4时,可将直线AE的方程表示为y-y■=■(x-x■),结合y■=4x■可整理为y=■x-1,显然直线AE恒过点F(1,0);当y■=4时,可将直线AE的方程表示为x=1,显然同样恒过点F(1,0). 综上可知直线AE恒过一定点,且定点坐标为(1,0).
②该问探究△ABE面积的最小值,可将三角形视为以AE为底、点B为顶点的三角形,则其面积可以表示为S△ABE=■AE·d(其中d表示顶点B到底边AE的距离).
由①问可知直线AE过定点F(1,0),则AE=AF+FE=x■+■+2,设直线AE的方程为x=my+1,点A位于直线AE上,则有m=■.设点B的坐标为(x■,y■),整理直线AB的方程可得x=-■y+2+x■,代入抛物线方程可得y2+■y-8-4x■=0,可求得y■=-y■-■,x■=■+x■+4. 点B到直线AE的距离可以表示为d=■=4■+■,所以S△ABE=■AE·d=■x■+■+2·4■+■=2■+■3≥16,当且仅当x■=■,即x■=1时等号成立,所以△ABE的面积存在最小值,且最小值为16.
关于问题的解后思考
上述是对一道圆锥曲线问题的探究过程,其中第(2)问的两小问具有一定的代表性,下面对其进一步反思.
1. 考题突破的关键步骤
题目是高考常见的圆锥曲线问题,其核心之问为第(2)问的两小问,分别探究直线过定点和面积的最值. 其中第①问的关键一步是确定点E的坐标,需要结合题目中的条件将其表示,上述设出点A的坐标,采用信息直译的方式,按照“直线AB斜率→直线l方程→直线l■方程→点E坐标”的思路完成构建. 而第②问突破的关键有两个:一是如何构建三角形的面积模型,转化为面积函数;二是如何研究函数的最值. 上述充分利用了点到直线的距离公式及不等式的性质来完成上述关键点的突破.
2. 考题突破的解法启示
总体而言,上述圆锥曲线考题为存在性探究题,从直线过定点和面积最值的探究过程来看,数形结合是突破的有效策略,采用假设验证方法是突破的基本思路,将问题转化为关于核心变量的数式则是解析的目标. 其中核心变量的设定将直接关系到问题数式构建的复杂度,存在性问题的核心在于求出其中的未知量,故设定核心要素时可以此为依据.另外核心变量求解时可采用如下方法:①直接利用其中的条件和辅助变量表示,②联立核心变量与已知条件,构建求解方程,利用方程思想来表示核心变量.
3. 考题变式的拓展方向
开展考题变式是提升学生思维的重要方式,同时可引导学生深刻认识考题,以上述试题为例,具有多个拓展方向,除了可以对其最值进行逆向思维命题外,还可以结合三角形的周长、角度特性进行变式.
变式1:当△ABE的面积为16时,求点A的坐标.
解析指导:该变式与原问题突破思路一致,构建面积模型,转化为关于点坐标参数的面积方程,解方程即可.
变式2:△ABE是否可以为直角三角形?若可为直角三角形,试求点A的坐标;若不可以,请说明理由.
解析指导:直角三角形中一内角为90°,条件没有设定直角需要对其加以讨论,构建方程的依据有如下几种:①勾股定理,②交叉直线斜率之积为-1,③向量之积为0. 从简化过程角度来看建议采用后两种构建方式.
探究性问题的教学建议
1. 引导学生明晰探究性问题的指向
圆锥曲线探究题能够全面考查学生的知识水平和思维能力,因此备受出题人青睐,而在实际学习时需要引导学生明晰探究性问题的命题指向,包括基本形式、考查内容、突破思路等. 例如探究性问题常出现“是否”“有且只有”“探究”等词汇,主要考查曲线的位置关系、图形性质、向量数量积、数式变形等内容,突破时可采用假设论证的思路. 解题教学中不仅应重视问题转化的过程,还应注重引导学生体会探究性问题的解析思路,帮助学生提升探究能力.
2. 引导学生形成数形结合的策略
圆锥曲线题最为显著的特点是融合了“数”与“形”,即将曲线解析式与图像有效地融合为一体,从数形角度来突破是最基础的策略,因此问题探究的过程有必要根据题意来绘制草图,探索图像结构,挖掘隐含信息,在此基础上排除干扰,提取图形,合理讨论. 例如上述考题的最后一问探讨三角形的面积,关键的一步是构建面积模型,结合图像来加以分析很容易确定模型构建的方式. 教学中要向学生传达数形结合解析问题的策略,使学生深刻体会数形结合的思想内涵,掌握数形结合方法的解析技巧.
3. 引导学生重视解后思考的变式
对考题进行拓展变式有助于学生全面认识问题,总结解题方法,拓展数学思维.解题教学帮助学生贯通思路后,学生对问题的脉络有了初步的了解,但思维仍停留在考题本身,并不能完全认清问题的结构,更无法把握其中的关键步骤和核心解法,此时需要教师合理设置变式问题,引导学生进行解后反思.在反思过程中重视对思路、解法的整合,将问题上升到类题层面,促进学生形成完善的解题策略,促进数学思维的发展.
