基于TI图形计算器的高中数学探究性教学研究

胡高嵩 肖启平

[摘  要] 基于TI图形计算器的高中数学探究性教学能够体现以生为本的理念，能够使学生充分经历知识的形成、发展和应用过程，有效改变传统的教学和学习方式. 文章在阐述高中数学教学引入TI图形计算器的价值的基础上，以“圆锥曲线中直线存在性问题”为例，探讨了基于TI图形计算器的高中数学探究性教学策略.

[关键词] 高中数学;TI图形计算器;探究性教学;策略

建构主义认为，新知识的获得就是典型的建构学习过程，而TI图形计算器具有几何画板、简单编程、数据处理、函数和数理实验等功能，不仅能够帮助学生将抽象的内容直观化展示，使高中数学课堂教学更加生动直观，而且也能帮助学生理解和掌握数学知识，有效突破教学重点与难点.在一定程度上可以认为TI图形计算器是解剖抽象复杂性数学知识的有力手段，因此，借助以TI图形计算器为核心的TI手持教育技术，探究高中数学探究性教学策略具有重要的意义.

高中数学教学引入TI图形计算器的价值

1. 有利于激发学生探究的兴趣

传统单一的教学方式往往致使学生学习兴趣淡薄，并且，随着几何画板等图形制作工具的引入，各种精美的图形以及动态的课件往往吸引了学生的注意力，但并没有从真正意义上促使学生专注、思考图形所蕴含的数学原理，在一定程度上分散了学生的注意力，而TI图形计算器的使用可以让学生在课堂教学中亲自动手操作、研究数学问题，可以通过学生指尖上的探究有效消除数学知识的神秘感，使学生与现实数学接触更加亲密，充分调动了学生学习的积极性.

2. 有利于突破教学重难点知识

提供丰富的感性材料是理解抽象概念的重要途径，而TI图形计算器能够将抽象的知识通過直观、动态、形象的方式呈现，能够有效启迪学生的思维，从而突破教学过程中的重难点知识. 并且，还可以将某个学生的TI图形计算器呈现到电脑中进行全班演示和深刻剖析. 例如，教师可以针对某一学生典型的错误解法将其投影到大屏幕中进行深刻解读，可以就一题多解中学生独到的解法进行相互借鉴展示成果.

3. 有利于培养学生的合作探究能力

小组合作探究是TI图形计算器使用过程中常用的模式，并且，TI图形计算器具有超强的表现力和良好的重现力，既能亲自动手操作，又能看得见所呈现的信息.与此同时，教师也从知识的传播者转变为问题的组织者、发现者、探究者和合作者，显然，这种的教学模式有利于培养学生的合作交流和探究能力.

4. 有利于提高学生学习数学的效率

TI图形计算器有效打破了传统黑板静态展示的教学模式，不仅可以常规作图，还可以动态演示和变换，能够直观地表现出问题的数与形之间的内在联系，并且，还可以通过无线接收装置实现课堂中师生之间的实时互动，还可以创设教学情境，将学生作答结果反馈到电脑中进行统计分析，有针对性地进行个性化教学. 同时，教师可以从TI图形计算器动态窗口中了解每个学生的操作过程和进度[1]，关注每个学生是否专注课堂，并及时给予提醒和帮助.

基于TI图形计算器的高中数学探究性教学实践

仅有相关理论是不够的，而基于TI图形计算器的高中数学探究性教学理应是理论联系实际的. 圆锥曲线中的直线存在性问题历来是教学中的重难点知识，相当数量的学生对于该类问题常常望洋兴叹，因此，本文以圆锥曲线中的直线存在性问题为例，充分应用TI图形计算器这个探索发现、获得知识的平台，探索高中数学探究性教学策略.

1. 预习自测，引入新课

为了引发学生主动参与课堂教学，有效将学生的思维集中在将要探究的圆锥曲线直线存在的问题上来，笔者设计了如下预习自测题目：

（1）已知椭圆■+■=1的弦被点（4，2）平分，试求该条弦所在的方程.

（2）已知椭圆9x2+16y2=144与直线l：y=x+m有公共点，m的取值范围能不能确定？若能确定，则m的取值范围是多少？若不能确定，则说明你的理由.

在此过程中，教师应通过引导的方式，鼓励学生类比圆锥曲线及其性质，大胆说出自己的解题思路，了解学生对点差法、韦达定理等基本知识的掌握.

2. 利用工具，尝试探究

为了将抽象的知识变得更加直观形象，促使学生利用TI图形计算器图像功能轻松推导出圆锥曲线中所要求解的直线上来，教师应及时引入TI图形计算器，利用TI图形计算器无线系统的功能发送如下题目：

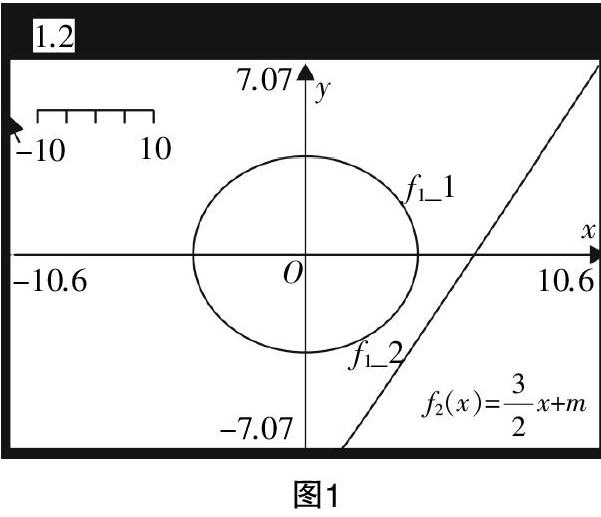
已知直线l：y=■x和椭圆C：■+■=1，试问是否存在平行于直线l的直线p，并且使得这两条直线之间的距离为4，直线l与椭圆C：■+■=1有公共点？？摇

随后，要求学生应用常规思路解答，即不妨存在这样的直线p：y=■x+m，使得直线l与椭圆C：■+■=1有公共点，直线l与直线p之间的距离为4，从而探究是否存在这样的m.

显然，上述探究过程费时费力，探究过程较为抽象，不利于学生对重难点知识的掌握，并且相当数量的学生已经遗忘两平行线之间距离的计算公式.  此时，教师提出疑问，能不能借助TI图形计算器将上述思路直观化，进而转入本节课程重点，即如何通过TI图形计算器形象直观地呈现上述探究结构. 于是，教师应及时引导学生在探究过程中引入TI图形计算器，尝试TI图形计算器的解法，如图1所示，并通过问答的方式促使学生在动手操作过程中感受椭圆与直线之间的公共点个数.

基于以上分析，学生对于如何利用TI图形计算器解答圆锥曲线中直线存在问题有了一定的了解，但仍然有相当数量的学生无法准确归纳出存在性问题的解题步骤，因此，教师应设计如下变式练习题目，要求学生以小组讨论的形式，利用TI图形计算器求解. 如图2所示，将结论落实到具体学案上，不断培养学生科学的思维品质和自主学习的能力.

已知双曲线x2-y2=1，是否存在直线l，使得直线l经过点A（2，1），直线l与双曲线相交于P，Q两点，并且PA=AQ？

3. 归纳小结，回顾反思

归纳总结是探究性教学不可缺少的一个重要环节，为了有效培养学生反思学习的习惯，最大限度地鼓励学生对TI图形计算器解决相关问题进行质疑和概括[2]，教师应引导学生从知识和方法两个方面总结本节课程所学内容，在具体实践中，教师应设计如下问题引导学生进行归纳和概括.

（1）TI图形计算器在学习探究中给了我们什么样的启示？

（2）在本节课程中，你学习到了哪些知识与方法，这些知识与方法之间有哪些联系与区别？

（3）如何利用TI图形计算器探究出圆锥曲线中直线存在性问题.

同时，深入反思上述教学过程，作为教学的主导者，有以下两个方面有待进一步提升：一是课堂教学进展缓慢，相当数量的学生对于TI图形计算器的热情很高，但是对其计算器相关功能不熟练，部分学生对计算器操作较慢，并且由于条件的限制，学生只能以小组的形式拥有TI图形计算器，因此，教师应最大限度地展示TI图形计算器的功能，并在TI图形计算器有限的情况下，最大限度地轮流使用计算器，实施滚动式培训. 二是课堂驾驭能力不足，由于相当数量的学生误认为实验课就是让自己去做，学习态度往往不够认真，因此，教师应引导学生端正自己的学习态度，要向其他同学或老师学习，促使学生认为相比普通课堂教学，实验课堂教学更容易学到更多的知识.

总之，基于TI图形计算器的高中数学探究性教学能够体现以生为本的理念，能够使学生充分经历知识的形成、发展和应用过程，有效改变传统的教学和学习方式. 我们相信，随着TI图形计算器在高中数学中的不断实践与探究，TI图形计算器定能充分发挥其强大的优势，定能不断提高学生发现问题、解决问题等数学核心素养.

参考文献：

[1]  王竹婷. TI-Nspire手持技术在文科圆锥曲线课堂教学中的实践[J]. 中学数学研究（华南师范大学版），2013（06）.

[2]  高鹏，李师师，常磊.基于图形计算器开展高中数学实验探索[J]. 中国数学教育，2019（Z2）.