雷达误差对船舶碰撞危险预警性能的影响
2020-10-20魏祥渊王兴华李丽娜郭健
魏祥渊 王兴华 李丽娜 郭健


摘要:鉴于船舶碰撞危险预警的准确性依赖前端雷达的精度,即雷达误差可能导致危险误判,分析雷达误差对船舶碰撞危险预警性能的影响。分析雷达目标参数计算和船舶碰撞危险判断的原理,建立雷达误差的传递公式;运用概率理论计算雷达误差可能导致预警模型发生误判的概率,进而评估其碰撞危险预警的准确性。以江苏镇扬汽渡船航行避碰智能预警系统为例,评估3种不同精度的雷达对其预警准确性的影响,论证了系统现用雷达的精度能够满足镇扬汽渡船预警准确性的需求。
关键词:雷达误差; 碰撞危险预警; 误判; 预警准确性
中图分类号: U676.1
文献标志码:A
Effect of radar error on ship collision risk early warning performance
WEI Xiangyuan, WANG Xinghua, LI Lina, GUO Jian
(Navigation College, Jimei University, Xiamen 361021, Fujian, China)
Abstract:
In view of the fact that the accuracy of the ship collision risk early warning depends on the accuracy of front-end radars, that is, the radar error may lead to risk misjudgment, the effect of radar error on the ship collision risk early warning performance is analyzed. The transmission formula of radar error is established by analyzing the principles of the radar target parameter calculation and the ship collision risk judgment. The probability theory is used to calculate the probability that the radar error may lead to the misjudgment of the early warning model, and the accuracy of its collision risk early warning is evaluated. Taking the collision avoidance intelligent early warning system of Zhenyang steam ferries in Jiangsu Province as an example, the effect of three kinds of radars with different precision on the early warning accuracy is evaluated. It is proved that the accuracy of the radar used in the system can meet the requirement of early warning accuracy of Zhenyang steam ferries.
Key words:
radar error; collision risk early warning; misjudgment; early warning accuracy
0 引 言
準确的船舶碰撞危险预警是船舶安全航行的重要保障,更是船舶进行有效避让的前提。预警的准确性主要依托两个方面,一是科学合理的碰撞危险评判模型[1-3],二是精确可靠的传感器数据,这两方面相互独立又相互影响。要建立科学合理的碰撞危险评判模型必须考虑前端传感器数据精度不高所导致的误判。
目前,获取目标船动静态数据的主要来源为船舶自动识别系统(automatic identification system,AIS)和雷达[4]。然而,并非所有的船舶均安装或开启了AIS,因此若要获得船舶航行水域所有船舶的数据,雷达还是主要的数据来源[3]。然而,雷达的不足之处显而易见,即存在雷达误差。雷达误差可能引起预警模型发生危险误判,因此有必要验证所使用的雷达精度能否满足预警模型的要求。关于雷达误差对船舶碰撞危险预警性能的影响的研究并不多,文献[5]对由雷达噪声引起的相对误差进行了分析,文献[6]对雷达距离测量精度进行了评估,但都未涉及对危险预警的分析。文献[7]对雷达测绘中方位和距离的偶然误差进行了初步估算,并在估算数值的基础上分析了最近会遇距离
(distance at closest point of approach,DCPA)
可能产生的最大相对误差,但是这种方法适用于当时的人工标绘,不太适用于雷达自动标绘。文献[8]分析了雷达测算中来船航向、航速的误差来源,对来船的航向、航速误差可能导致的碰撞危险进行理论分析,但是并未通过实测或者仿真实验进行验证。本文将理论分析与仿真实验相结合,通过分析雷达目标参数计算和船舶碰撞危险判断的原理,建立雷达误差的传递公式,运用概率理论计算雷达误差导致预警模型发生误判的概率,进而论证雷达误差是否能够满足预警模型的要求。
1 雷达目标参数计算和船舶碰撞危险判断的原理
1.1 雷达目标参数计算原理
雷达目标参数为DCPA和最短会遇时间(time for closest point of approach,TCPA),分别记为dCPA和tCPA,其计算流程见图1。
雷达自动跟踪录取的目标,当跟踪达到稳定收敛后(有一定的跟踪延迟),预测位置与实测位置基本一致,也即跟踪窗的运动规律与目标的运动规律基本一致。因此,可用跟踪窗的运动参数替代目标的运动参数[9]。
dCPA和tCPA的計算方法[10]如图2所示:称目标船相对速度矢量
[WTHX]V[WTBX]r的延长线为相对运动线,以本船O向相对运动线作垂线OC,则C为最近会遇点,线段OC的长即为dCPA,目标船自T点至最近会遇点C的航行时间即为tCPA。图2中:R为目标船与本船的距离;
[WTHX]V[WTBX]O和
[WTHX]V[WTBX]T分别为本船和目标船的速度。
α可由目标船的相对航向φr和相对方位角Br表示,即
1.2 船舶碰撞危险判断原理
《1972年国际海上避碰规则》(以下简称《规则》)第8条“为避免与他船碰撞而采取的行动,应能导致在安全的距离驶过,……”中的安全距离即为安全会遇距离(safe distance of approach, SDA),用dSDA表示。显然,碰撞危险和安全会遇距离在《规则》中都是模糊的概念。实际上,安全会遇距离dSDA的确定与船舶的尺度、航速、操作性能、通航环境等因素有关。若要实现准确的船舶碰撞危险预警,必须研究两船最近会遇距离dCPA处于什么范围内存在潜在碰撞危险。
目前估算安全会遇距离的基本思路是:安全会遇距离dSDA是本船与他船在保向保速情况下的最近会遇距离dCPA,在碰撞区域外,且留有本船的操纵余地[11]。碰撞区域是以本船为中心,不考虑操纵余地,只考虑两船尺寸大小、会遇态势而产生的区域。
两船进入该区域交会就会发生碰撞,故称该碰撞区
域半径为临界碰撞会遇距离(dSDA_min),见图3[3]。
图3中:A点为本船雷达所在位置;B点为目标船的中心;L0和L1分别为本船和目标船的船长。因为船舶尺度和会遇态势实时变化,所以dSDA_min是一个动态的数值。
江苏镇扬汽渡船航行避碰智能预警系统安全会遇距离dSDA边界模型见图4。dSDA是在dSDA_min基础上加上两船安全通过时船舶边缘的最小富余量(dSM)得到的。dSM的取值是向有经验的船长和驾驶员进行问卷调查获得的,定义为根据本船和目标船的船长、速度,在不同会遇局面及不同航行水域过船首或过船尾或过正横时,两船不采取避让措施且能够通过时两船边缘的最小容忍距离。因为船舶尺度、会遇态势的不同,dSM的取值也不尽相同,所以dSDA也是一个实时变化的数值。
dCPA与dSDA的关系见图5。通常将被跟踪目标的dCPA与设置的dSDA进行比较来判断会遇船舶是否
存在潜在碰撞危险。具体判断方法为:(1)当dCPA≥dSDA时,来船为非危险目标;(2)当dCPA
船舶碰撞危险判定方法:(1)当dCPA
2 雷达误差对船舶碰撞危险预警准确性的影响
2.1 雷达误差传递公式
由式(3)可知,最近会遇距离dCPA的误差受两船距离R、目标船相对航向φr和目标船相对方位角Br误差的影响。
假设两船距离R的最大误差为eR,其均方根误差为emR,某些情况下取最大误差为2倍的均方根误差(置信概率为95.45%),但一般情况下取最大误差为3倍的均方根误差(置信概率为99.73%),即
同理,假设:φr的最大误差为eφr,其均方根误差为emφr;Br的最大误差为eBr,其均方根误差为emBr;最大误差均为3倍的均方根误差。
R的误差分别与φr、Br的误差相互独立;φr的误差与Br的误差具有相关性,假设ρ为这2个误差之间的相关系数(根据所测数据求得皮尔逊相关系数ρ≈-0.76)。
根据误差传递规律[12],式(3)中的dCPA的均方根误差为
其最大误差为
2.2 雷达误差导致预警系统误判的概率
由雷达测算得到的dCPA为已知量,而真实的dCPA为未知量(用d*CPA表示),由于edCPA的存在,d*CPA与雷达测算的dCPA存在如下关系:
2.2.1 虚警概率
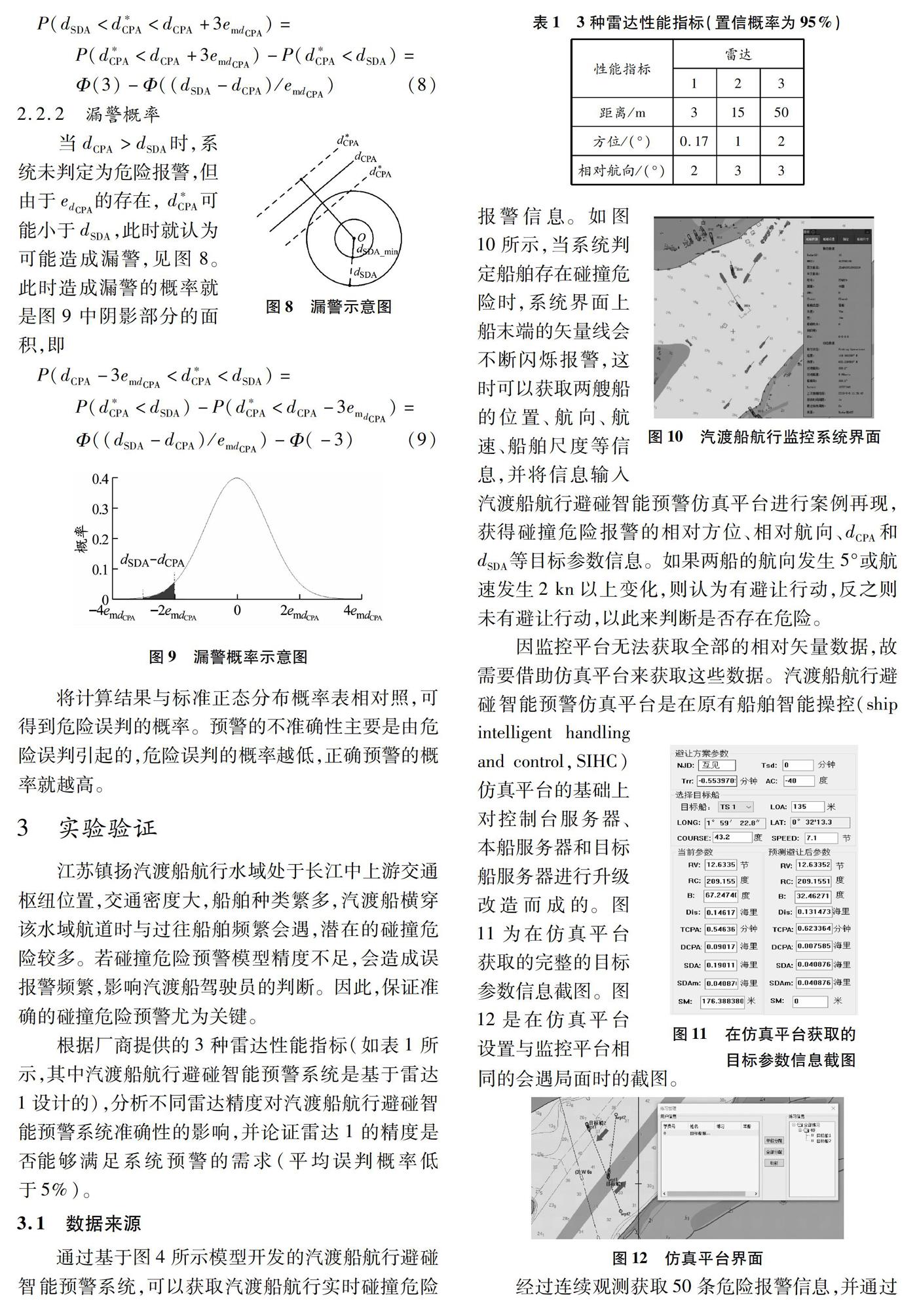
当dCPA 日本学者今津隼馬等[13]的研究表明,d*CPA的误差服从正态分布(见图7),即d*CPA服从N(μ,σ2),其中: 一般认为,d*CPA在(dCPA-3emdCPA,dCPA+3emdCPA)范围内取值,当d*CPA>dSDA时,就认为可能存在虚警,由正态概率分布可知,其虚警的概率就是图7中阴影部分的面积[14],即 2.2.2 漏警概率 当dCPA>dSDA时,系统未判定为危险报警,但由于edCPA的存在, d*CPA可能小于dSDA,此时就认为可能造成漏警,见图8。 此时造成漏警的概率就是图9中阴影部分的面积,即 将计算结果与标准正态分布概率表相对照,可得到危险误判的概率。预警的不准确性主要是由危险误判引起的,危险误判的概率越低,正确预警的概率就越高。 3 实验验证 江苏镇扬汽渡船航行水域处于长江中上游交通枢纽位置,交通密度大,船舶种类繁多,汽渡船横穿该水域航道时与过往船舶频繁会遇,潜在的碰撞危险较多。若碰撞危险预警模型精度不足,会造成误报警频繁,影响汽渡船驾驶员的判断。因此,保证准確的碰撞危险预警尤为关键。 根据厂商提供的3种雷达性能指标(如表1所示,其中汽渡船航行避碰智能预警系统是基于雷达1设计的),分析不同雷达精度对汽渡船航行避碰智能预警系统准确性的影响,并论证雷达1的精度是否能够满足系统预警的需求(平均误判概率低于5%)。 3.1 数据来源 通过基于图4所示模型开发的汽渡船航行避碰智能预警系统,可以获取汽渡船航行实时碰撞危险报警信息。如图10所示,当系统判定船舶存在碰撞危险时,系统界面上船末端的矢量线会不断闪烁报警,这时可以获取两艘船的位置、航向、航速、船舶尺度等信息,并将信息输入汽渡船航行避碰智能预警仿真平台进行案例再现,获得碰撞危险报警的相对方位、相对航向、dCPA和dSDA等目标参数信息。如果两船的航向发生5°或航速发生2 kn以上变化,则认为有避让行动,反之则未有避让行动,以此来判断是否存在危险。 因监控平台无法获取全部的相对矢量数据,故需要借助仿真平台来获取这些数据。汽渡船航行避碰智能预警仿真平台是在原有船舶智能操控(ship intelligent handling and control,SIHC)仿真平台的基础上对控制台服务器、本船服务器和目标船服务器进行升级改造而成的。图11为在仿真平台获取的完整的目标参数信息截图。图12是在仿真平台设置与监控平台相同的会遇局面时的截图。 经过连续观测获取50条危险报警信息,并通过平台仿真获取其相对矢量数据,由于篇幅有限,本文仅列出其中的10条,见表2。 3.2 实验结果分析 针对表1中雷达1,根据式(6)~(9)求得系统误判的概率,并比较不考虑误差与考虑误差的区别,见表3。 当测算的dCPA与dSDA接近时,误差对判定结果的影响很大,如果不考虑误差极易出现误判的情况,如危险报警5和7就分别为虚警和漏警。如果考虑误差,就可对每次判断给出误判的概率,如危险报警5发生误判的概率为38.08%、危险报警7发生误判的概率为21.64%,概率高意味着有较大可能发生误判,以此作为辅助判断,实际结果也证实危险报警5和7确实存在误判。 根据表1的3种雷达精度和50条危险报警信息求得系统误判的概率,结果见图13。 根据统计数据,50次记录中出现虚警和漏警各1次,预警准确性为96%。图13中:雷达1的平均误判概率为3.5%,计算结果与统计结果较为吻合,并且达到了平均误判概率低于5%的要求,其精度能够满足汽渡船航行避碰智能预警系统的需求;雷达2和雷达3的平均误判概率分别为12%和21%,其是否能够满足汽渡船航行避碰智能预警系统的需求,有待商榷。 4 结束语 本文通过建立雷达误差的传递公式,运用概率 理论,计算自主构建的船舶碰撞危险预警模型发生误判的概率,从理论上评估雷达精度对船舶碰撞危险预警系统性能的影响。以江苏镇扬汽渡船航行避碰智能预警系统为例,论证了现有雷达精度能够满足其预警系统的需求。限于时间及篇幅,本文仅讨论了雷达在稳定跟踪或船舶在保向保速情况下其精度对碰撞危险预警的影响,本船和目标船大幅度机动或雷达未稳定跟踪等的影响,有待日后进一步研究。 参考文献: [1]章泽虎. 基于模糊综合评判的船舶碰撞危险度模型[D]. 大连: 大连海事大学, 2012. [2]苏鹏. 港口水域船舶碰撞危险预警模型及应用[D]. 厦门: 集美大学, 2015. [3]高建杰. 镇扬汽渡水域船舶碰撞危险智能预警研究[D]. 厦门: 集美大学, 2018. [4]张翼周. 新体制民用航海雷达的应用与发展[J]. 电讯技术, 2014, 54(6): 857-862. [5]ZHANG Yunpeng, YI Fan, KONG Wei. Analysis of relative error in detection caused by signal-induced noise in Na lidar system[J]. Science China Earth Sciences, 2018, 61(1): 109-118. [6]SCHERR S, AFROZ R, AYHAN S, et al. Target evaluation for high accuracy 80 GHz FMCW radar distance measurements[C]//IEEE Topical Conference on Wireless Sensors and Sensor Networks. IEEE, 2017: 11-14. [7]胡玉琦. 应用雷达绘算求来船最近会遇距离的误差[J]. 大连海运学院学报, 1979(2): 54-61. [8]张志新, 李佳初, 高善明. 雷达避碰中误差理论的应用[J]. 中国航海, 1991(1): 56-62. [9]王世远. 船用导航雷达[M]. 大连: 大连海事大学出版社, 2014: 232-237. [10]刘彤. 航海仪器[M]. 大连: 大连海事大学出版社, 2013: 101-107. [11]李丽娜. 船舶自动避碰研究中安全会遇距离等要素的确定[J]. 大连海事大学学报, 2002, 28(3): 23-26. [12]钱政, 贾果欣, 吉小军, 等. 误差理论与数据处理[M]. 北京: 科学出版社, 2013: 79-83. [13]今津隼馬, 小山健夫. 避航開始時機の決定について[C]//日本航海学会第69回講演会にて講演. 東京: 日本航海学会, 1984: 31-37. [14]同济大学应用数学系. 工程数学[M]. 上海: 同济大学出版社, 2002: 296-318. (编辑 赵勉) 收稿日期: 2019-08-28 修回日期: 2019-12-04 基金项目: 国家自然科学基金(51879119) 作者简介: 魏祥渊(1993—),男,福建三明人,硕士研究生,研究方向为交通信息工程及控制,(E-mail)843384150@qq.com; 王兴华(1985—),女,河南新乡人,硕士,助理实验师,研究方向为交通信息工程及控制,(E-mail)yuxia01001@163.com; 李丽娜(1962—), 女, 福建泉州人,教授,硕导,研究方向为交通信息工程及控制,(E-mail)lln668@163.com
