黄土质高填方路基沉降变形与预测

杨三强，段士超，刘娜，吴浩楠

(1.河北大学 建筑工程学院,河北省土木工程监测与评估技术创新中心 河北 保定 071002；2.河北建设集团股份有限公司 路桥公司，河北 保定 071070)

高填方路基因填料和上部荷载的复杂作用，常造成路基不均匀沉降变形.针对高填方路基沉降建立一种精确的沉降预测模型，能够为具体施工提供参考，有效保障高填方路基的施工质量.朱才辉等[1]通过对吕梁机场进行施工过程的监测，对路基填土高度因素影响高填方沉降进行了分析.姚仰平等[2]考虑时间与应力的共同影响，得出了一维蠕变沉降计算方法.万志辉等[3]针对道路路基的沉降差异进行了研究，总结出路基沉降差异规律.Kanayama等[4]在双曲线模型下进一步建立了一种拓展双曲线法，并对路基进行沉降预测.杨超等[5]根据现场高填方工后沉降实测数据，分析了各种数学模型对于沉降拟合的适用性.王海英等[6]利用三点法与双曲线法共同拟合减小误差提高精度，得到一种三点修正双曲线模型.

延崇高速河北段建设地区为张家口地区，年降雨量偏大，且常年气温偏低，使得路基土体中含水率较高.加之该地区黄土土质因素，极易造成路基沉降过大，对高填方路基造成破坏.基于此，本文依托河北省住建厅科技项目“冀西北地区湿陷性黄土高填方路基稳定性研究”项目，借助施工现场路基沉降监测手段，用曲线模型对监测数据进行拟合，再与数值模拟结合验证，最终构建出高填方路基沉降数学模型.该研究成果可为延崇高速公路高填方路基设计及施工提供理论支撑与技术指导，具有重大工程价值.

1 工程概况

延崇高速河北段ZT5标段，地处张家口赤城县，境内群山环绕，沟壑纵横.该地区年均降水量424 mm左右，年平均气温5.5 ℃.该标段K45+360-K49+600桩号中分布有湿陷程度轻微-中等的黄土，长度约4.24 km.K46+500桩号处为工程中最高填方路基，填方总高度达30.322 m.为保证工程的安全质量，并及时掌握黄土质高填方路基填筑过程中和过程后的沉降量问题，所以选取K46+500断面处为典型高填方路基断面进行研究，对其采取沉降监测.该断面填土以粉砂土和黄土为主，平均含水率为19%，塑性指数为15.

2 监测方案及数据

现场埋设3个沉降监测桩，3个点分布在K46+500处高填方路基顶面的路肩处，相隔15 m 1个，编号1～3，图1为监测桩位布置的主视图a和侧视图b.

a.主视图;b.侧视图

对3个沉降监测桩进行每隔15 d 1次的定期监测，记录沉降数据，如表1所示.

表1 K46+500处监测桩的累计沉降量Tab.1 Accumulated settlement of observation pile at K46+500

3 高填方路基沉降曲线拟合

曲线拟合法适应性比较强，拟合数值类型范围比较广，能对大量现场监测数据进行较好的拟合，建立预测模型[7].本文主要就对数曲线拟合法、乘幂曲线拟合法和双曲拟合法结合现场的实测数据，进行曲线拟合分析.

利用Origin软件对实测数据建立拟合曲线，对比3种拟合法的拟合程度，拟合曲线的相关系数R2越接近于1，说明拟合效果越高.计算得出预测模型，将预测沉降与实测数据对比，选取对高填方路基沉降最优拟合法及预测模型.

3.1 对数拟合法

将沉降量S与时间t的关系，视为按对数规律变化[8].表达式为

S=alnt+b，

(1)

式中，a、b为系数.

将现场沉降监测数据带入方程式，可求出a和b的值，得到完整表达式，因此可以用该式计算任意时间t对应的沉降量.

将实测数据进行对数曲线拟合，拟合曲线如图2.

由图2可知：3个桩号实测值的对数曲线拟合方程和拟合优度结果，1号桩沉降的拟合方程为S=15.168 2lnt-27.863 5，相关系数R2=0.998 6；2号桩沉降的拟合方程为S=19.545 1lnt-33.799 2，相关系数R2=0.999 2；3号桩沉降的拟合方程为S=18.546 4lnt-31.831 8，相关系数R2=0.999 4.

3.2 双曲线拟合法

将沉降量S与时间t的关系视为按双曲线规律变化[9]，表达式为

(2)

式中，St为某一时间t对应的路基沉降量，S0为初始路基沉降量，a、b为系数.

式(2)可转化为

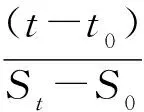
(3)

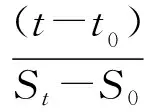
将实测数据进行双曲线拟合，拟合曲线如图3.

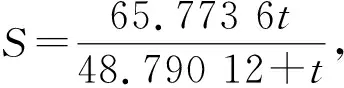
图3 双曲线拟合曲线Fig.3 Hyperbolic curve fitting curve

3.3 乘幂曲线拟合法

将沉降量S与时间t的关系,视为按乘幂曲线规律变化[10].表达式为

St=atn,

(4)

式中,St为某一时间t对应的路基沉降量，a为系数，n为幂指数.

对式(4)两边求对数，得到

lnSt=lna+nlnt.

(5)

令lnSt=c, lna=d,代入式(5)，得到

c=d+nlnt.

(6)

由式(6)可知d和n分别为c-lnt关系曲线中的截距和斜率，即可得到a、n,代入式(4)，可以计算出时间t对应的沉降量.

将实测数据进行乘幂曲线拟合，拟合曲线如图4.

图4 乘幂曲线拟合曲线Fig.4 Power function curve fitting curve

由图4可知：3个监测桩实测值的乘幂曲线拟合方程和拟合优度结果，1号桩沉降的拟合方程为S=4.122 09×t0.524 36，相关系数R2=0.985 37；2号桩沉降的拟合方程为S=5.484 16×t0.514 09，相关系数R2=0.988 77；3号桩沉降的拟合方程为S=5.304 21×t0.510 85，相关系数R2=0.989 21.

4 预测模型对比分析

4.1 相关系数

对比3种拟合方法对每个监测桩沉降数值拟合结果的相关系数，结果见表2.

表2 沉降拟合结果Tab.2 Settlement fitting result

通过比较表2得出，3种拟合方法的拟合相关系数都很高，都在0.98以上接近于1，其中对数曲线和双曲线2种拟合模型的拟合相关系数都在0.99以上，拟合程度更高.3种拟合方法的相关系数说明了这3种方法对高填方路基短期沉降都能做出较为准确的拟合，长期沉降的预测有待研究.

4.2 精度对比分析

为进一步分析出各模型的预测精度，选取1号桩的沉降为例，将各模型的预测数值与现场实测值进行对比分析，结果如表3所示.

表3 1号桩各模型预测值与实测值比较Tab.3 Pile 1 comparison of predicted and measured values

计算出各模型预测值与实际值的误差平方和，结果如表4所示.

表4 各模型误差平方和Tab.4 Sum of squares of each model error

根据3种曲线拟合方法的误差平方和可知，3个预测模型中双曲线模型的误差平方和最小，为4.09 mm2，说明该模型预测值与实际监测值更接近，预测模型更加可靠.

4.3 沉降预测

经过预测模型的拟合相关系数对比和预测值与实测值的误差平方和对比，得出双曲线预测模型的预测精度更高，能对该高填方路基进行较准确的实时沉降预测.

5 数值模拟分析

采用FLAC3D软件对高填方路基进行数值建模分析，得出路基沉降值，对比预测模型的预测值.模型尺寸与实际工程K46+500断面处的高填方路基一致，长78.644 m，高38.322 m，宽度20 m，其本构模型为摩尔库伦模型，边界条件为X方向全部约束，Y方向全部约束，Z方向底部约束，建模初始模型如图5.本文通过路堤3次堆载的方式进行模拟，并在模拟计算过程中记录实际监测1号桩所对应模型点位(10，5，38.322)的沉降，计算结果如图6.

图5 初始模型Fig.5 Initial model

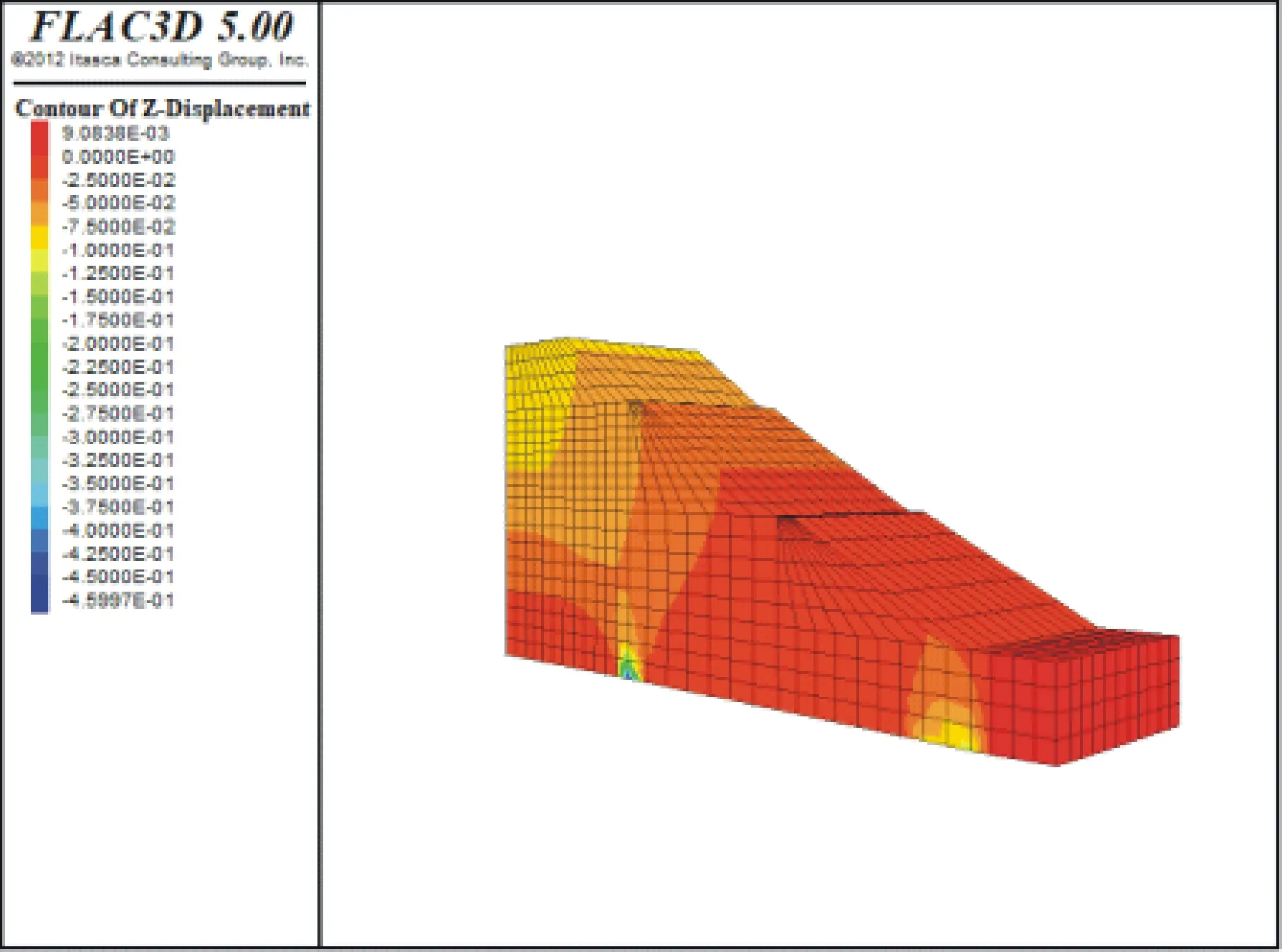
图6 计算后模型Fig.6 Post-computational model

利用FLAC3D中监测功能，对模型中(10，5，38.322)点进行沉降监测记录.该模型完成计算后调取其沉降监测结果，得到监测点的最终沉降量为65.833 mm.

利用双曲线模型模拟出监测1号桩处的最终沉降值为60.1 mm，与数值模拟出的65.833 mm，误差值为5.733 mm，相对误差为8.6%，经过数值模拟计算验证双曲线预测模型的预测值可靠.

6 结论

通过对黄土质高填方路基进行沉降监测数据分析，对数据内在规律进行归纳，通过3种曲线拟合对比分析，总结监测值的规律性，进而预测高填方路基工后沉降，得出以下结论：

1)通过利用origin软件对所选取的对数曲线模型、双曲线模型、乘幂曲线模型3种沉降预测模型进行数据拟合，3种曲线拟合的相关系数都在0.98以上，都能对该高填方路基短期沉降做出准确预测.

2)对3种预测模型的预测结果值与实测值比较分析，得出双曲线模型的预测结果值与实测值之间的误差值最小，预测精度最高，更能准确地预测沉降.

3)通过建立的双曲线预测模型对高填方路基沉降进行最终沉降预测，得出路基在517 d时沉降速率为0.01mm/d，沉降达到稳定.

4)通过利用FLAC3D软件对高填方路基进行数值模拟分析，对比双曲线预测模型与数值模拟计算出1号桩的最终沉降值，验证了双曲线模型的可靠性.