单元式超前液压支架偏转自复位机构及有限元分析
2020-10-20李提建刘新华
李提建,刘新华
1天地科技股份有限公司开采设计事业部 北京 100013
2中煤科工研究院有限公司 北京 100013
超 前液压支架主要分为两大类,一类为采用四连杆或套筒式稳定机构的超前液压支架,另一种为不带稳定机构的单元式超前支架[1-2]。超前液压支架在使用中多存在 2 个突出的问题,一是移架时对顶板反复支撑破坏[3-4];二是当巷道顶、底板凹凸不平或拱形巷道时,存在接顶效果差,对巷道的支护不理想。
对比具有稳定机构的超前支架,单元式支架具有结构简单、小巧轻便的特点,适宜用小车或单轨吊搬运,从而避免了因移架反复支撑带来的顶板破坏,是极具发展潜力的一种架型[5]。
单元式超前支架和普通超前支架一样,顶梁和其他部件间通过销轴销接,顶梁的偏转角度很小,适应顶板的能力不强;当遇到拱形巷道或巷道顶、底板凹凸不平时,接顶效果不理想,不能对巷道有效支护,且偏转载荷也会使销接件的受力状态变差,加速零部件的损坏,缩短支架寿命。
巷道在走向长度上顶板起伏变化较多,即使支架顶梁适应了当前的顶板状况,在下一次升架过程中若不能自动复位到水平状态,支架再次适应顶板变化的能力就会变弱。基于以上分析,研究单元式超前液压支架顶梁偏转机构和自复位机构,解决顶梁对顶板的适应性问题,对于促进超前支护装备的发展,改善超前支护状态具有重要意义。
1 顶梁偏转机构
单元支架由顶梁、底座和立柱组成。根据立柱数量可分为三立柱结构和两立柱结构。为了使超前支架小巧轻便,现多采用两立柱结构,如图 1 所示。
增加支架对巷道顶板的适应能力,就是要增大顶梁偏转角度。目前顶梁和立柱间多通过销轴连接,增大立柱销孔和销轴间的让位空间是最直接有效的办法。图 2 所示为在用的“纺锤销轴式”顶梁偏转机构。立柱上的柱头孔采用锥形对称结构,柱顶销两端采用纺锤形结构。该结构能够使顶梁偏转一定角度,改善了超前支架的接顶效果,适用于巷道顶板起伏不大的情况。
无论是柱头或销轴都有强度要求,这决定了“纺锤销轴式”结构的让位空间是有限的,太大的让位空间会损伤零件的强度。采用该结构的超前支架,当顶板起伏较大或拱形巷道时,接顶效果依然不好,而且该结构没有顶梁复位功能。

图1 单元式支架Fig.1 Unit hydraulic support

图2 纺锤销轴式偏转机构Fig.2 Spindle pinned def lection mechanism
为此,笔者提出了一种全新的顶梁偏转自复位机构,该机构进一步增大了顶梁的让位空间,且具有自复位功能,结构特点如图 3 所示:立柱球头的直径大于活柱杆体的直径,以保证顶梁大角度偏转后柱窝边线不会与活柱的外表面干涉;球头对称两侧设置 2 个平面卡槽,便于对弹性复位橡胶施加载荷。

图3 立柱球头结构示意Fig.3 Structure of bulb of column
新结构采用卡盘连接立柱与顶梁,如图 4 所示。竖向销轴将卡盘与顶梁柱窝处的连接耳固定,卡盘上的球面与立柱球头相配合,从而固定立柱球头。复位橡胶垫放置在卡盘内,通过螺栓与卡盘固定。当顶梁偏转时,立柱球头的平面卡槽对复位橡胶垫的受力面施加载荷,顶梁卡盘的限位块给复位橡胶垫提供支撑,复位橡胶垫变形;支架降架后,在复位橡胶垫弹力的作用下顶梁恢复水平姿态。采用新式的顶梁偏转自复位机构,顶梁最大可偏转 20°。
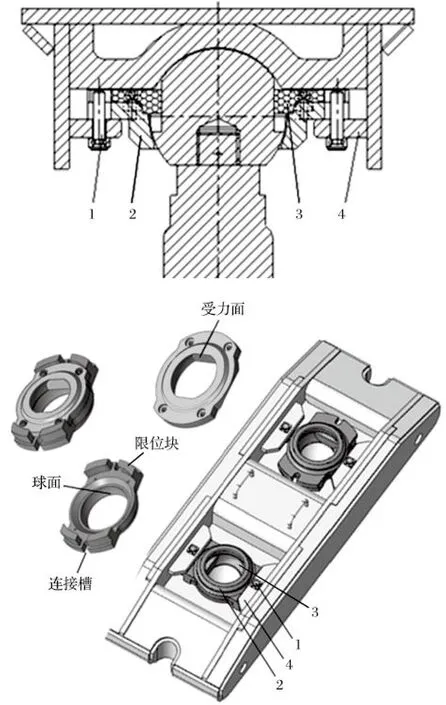
图4 立柱连接方式示意Fig.4 Column connecting mode
2 复位机构有限元分析
在顶梁发生偏转时,复位橡胶垫由于变形而存储弹性势能,供支架降架后顶梁自复位。该机构能否应用成功,很大程度上取决于复位载荷的大小。因此需要对复位橡胶垫进行分析,对复位载荷进行校核。
2.1 计算模型
复位橡胶垫材质为聚氨酯,具有超弹性能,是一种典型的非线性材料,一般认为其在未变形状态下是各向同性的,并认为是不可压缩材料。超弹材料的应力状态一般由弹性势能函数W对应变分量的导数来表示;所以其本构关系可用应变能密度函数表示,常采用 Mooney-Rivilin 模型[6-9]。Mooney-Rivilin 本构模型的应变能密度函数为

式中:C10、C01为材料常数;I1、I2分别为应变张量第1 和第 2 不变量。
弹性体的不可压缩参数

依据上述理论,采用有限元方法对复位橡胶垫进行分析。顶梁偏转时,卡盘、复位橡胶垫和立柱球头组成一个完整分析系统,且为载荷对称机构。所以取3 个零件的一半进行建模,如图 5 所示。

图5 复位机构有限元模型Fig.5 Finite element model of restoring mechanism
2.2 基于 MFC 法的载荷施加与接触处理
顶梁偏转带动卡盘和复位橡胶垫转动,橡胶垫的受力面和球头平面卡槽接触,复位橡胶垫变形。该过程中施加的是围绕球头球心的旋转位移,这一过程也等价于橡胶垫和卡盘不动,而球头绕球心旋转一定角度。笔者采用给球头施加角度位移的方法进行分析。
在有限元分析中,线位移比较好施加;围绕某一点的角位移需借助 MFC 法中的“刚性约束面”进行处理[10]。MFC 的刚性约束面法是指利用接触单元和技术,接触节点受导向节点 (目标单元) 的刚体运动所约束,通过多点约束方程形成刚性面,而刚性面的运动通过导向节点实现。具体实施方法为:在球心处额外建立 1 个单元并定义为导向节点,通过约束方程把导向节点和球头建立联系,球头跟随导向节点运动;对导向节点施加角度位移,便可实现球头绕球心的转动。
笔者选用 Solid185 单元,因其可用于模拟不可压缩和超弹材料分析,也可用于模拟可压缩材料的弹性分析。对于超弹材料,取=0.499 67;球头和卡盘的材料取=0.3;接触单元选用 CONTA173,目标单元选用 TARGE170;复位橡胶垫和卡盘及球头的接触定义为“标准接触”。
2.3 复位载荷分析
球头角度位移 15°时,复位橡胶垫的应力如图 6所示,复位机构位移如图 7 所示。复位橡胶垫一侧发生明显变形,其最大应力为 1 MPa,发生在球头平面卡槽棱边的接触处。

图6 复位橡胶垫应力云图Fig.6 Stress contours of restoring rubber pad
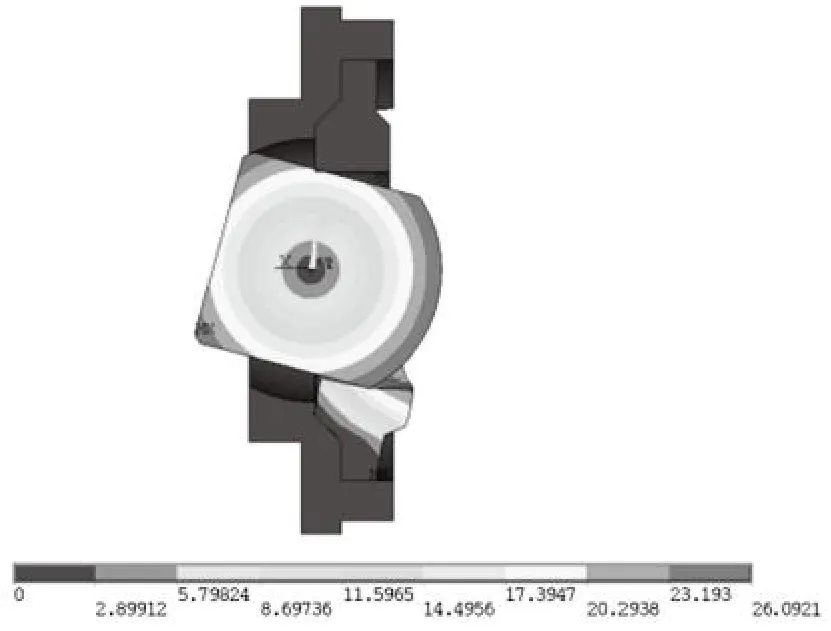
图7 复位机构位移云图Fig.7 Displacement contours of restoring mechanism
根据力的相互作用原理,复位橡胶垫接触单元的合力即为复位力;接触单元力对球心的合力矩即为复位力矩。接触单元的合力及对某点的矩可在后处理中根据命令 ETABLE、SPOINT 和 Fsum 求得。考虑球头的摩擦力,根据顶梁质量、球头半径和偏转角度可得出阻力距。取顶梁质量为 920 kg,球头半径为 100 mm。
顶梁偏转 3 种不同角度时的复位力如表 1 所列。

表1 不同偏转角度下的复位力Tab.1 The reset force table
分析表 1 数据可得:
(1) 顶梁偏转 5°、10°和 15°时,复位力距分别为 2.52×105、4.38×105和 6.4×105N·mm,均大于阻力距,说明顶梁可以复位。
(2) 顶梁偏转 5°、10°和 15°时,复位力矩与阻力距的比值分别为 1.05、1.47 和 1.81,表明顶梁偏转角度越大,复位效果越明显。这主要和阻力矩的组成有关。阻力矩由顶梁自身重力产生的阻力距和立柱球头的摩擦阻力矩组成。由于顶梁质量和球头半径均为定值,球头的摩擦阻力矩为定值,因此顶梁偏转角度较小时,复位橡胶垫的变形较小,复位力矩较小,但摩擦阻力矩不变,从而导致复位力矩与阻力矩的比值变小。
(3) 采用特殊的高强度弹性材料,增大C10和C01的值,可以进一步增大复位力矩。
3 结语
单元式液压支架是一种极具发展潜力的架型。基于该架型设计的顶梁旋转自复位机构,不仅进一步增大了顶梁的旋转角度,还可在下一次升架前自动使顶梁恢复水平姿态,从而提高了超前支架对顶板的适应性。
利用有限元 MFC 多点约束分析方法对复位机构进行分析,结果表明,复位力矩大于阻力距,顶梁能够复位。寻找特殊的高强度橡胶材料,可进一步提高复位力矩。后续还需进一步优化复位橡胶垫的结构。
