公路隧道上覆溶洞水压影响隧道稳定性的数值模拟研究

田荣生，张士朝

(1.镇巴县交通运输局，陕西 汉中 723600； 2.长安大学 公路学院，陕西 西安 710064)

0 引 言

在中国，岩溶现象主要集中在西南和中南地区。由于岩溶环境极不稳定，常常成为困扰隧道施工的主要地质问题[1]。在“西部大开发”和“一带一路”的背景下，中国西部的交通迅猛地发展，岩溶地区隧道的灾害治理成为主要的研究内容[2]。近几年，国内许多学者对岩溶地区隧道的灾害治理做了许多研究[3-6]，但尚有很多问题亟需解决。目前，常用的研究方法有理论分析、数值模拟及现场试验等[7]。

针对隧道上覆溶洞水压对隧道稳定性的影响，国内学者为了确定围岩变形规律而进行了深入的研究。曹洁等人[8-10]通过数值模拟和室内试验，探讨充水溶洞中水压对隧道围岩稳定性的影响，提出将实际工程中隧道底部围岩垂直方向上的位移变化作为事故发生的前兆。余小佳[11]采用有限元软件ANSYS计算和分析了不同位置、不同水压的溶洞分布在大跨度小净距隧洞左侧时的双洞围岩位移场、应力场，发现隧道双洞由水压溶腔引起的位移和压力变化在安全范围内，不会导致隧道结构产生破坏。马高强[12]采用ANSYS对其结构的受力特征和围岩的稳定性进行了研究，结果表明,水压力对隧道所受的轴力、弯矩、剪力影响最大。

本文通过采用三维数值模拟的方法，结合现场相关资料，建立不同溶洞水压的数值模型，分析围岩的位移和应力变化规律。

1 工程概况

S320省道星子山隧道及引线工程全长18.01 km，位于陕西省镇巴县；星子山隧道为单洞双车道隧道，洞径为12 m。隧道起讫里程为K7+330～K10+774，长3 444 m，属于特长隧道；海拔为896～1 570 m，相对高差约674 m。

隧址区属于构造剥蚀中山地貌区，地形起伏较大，山脊走向不规则，局部有陡峭孤峰，切割较深，形成许多狭窄的“V”形山谷，水系较发育，多急流，流水的侵蚀作用强烈，岩溶较发育。谷底高程为740～1 220 m，山顶标高约1 403～1 865 m，相对高差为180～1 130 m。山坡自然坡度为30°～50°，局部地段可达60°～70°，植被较茂密。

2 数值模型

2.1 建立模型

根据地层结构法和相关案例经验，依托工程地质、设计与施工情况，建立隧道几何模型，隧道跨度为12.0 m，高9.5 m；模型宽100 m，高100 m，隧道在模型中心；考虑溶洞的渗流区与隧道开挖掘进之间的相互联系，纵向长度取56 m。对溶洞进行简化设计，按照球体进行建模，位于隧道纵向长度中点，即28 m处，距离隧道3 m的上方位置。隧道模型采用映射网格的方式进行网格划分，如图1所示。

图1 模型概况

2.2 边界条件

模型下边界施加竖向位移约束，左右边界施加水平位移约束，前后边界施加轴向位移约束。考虑到溶腔的发育改变对附近围岩的影响，对地层模型进行初始应力场求解，选取“保留溶腔、消灭溶腔、施加溶腔水压”的方法，围岩采用了摩尔-库伦屈服法则，并且按照弹塑性模型进行计算。在开挖隧道时，考虑到溶腔内的水压力，模型采用渗流模式，同时设置了相当的水压力，由推算出的实际围岩的孔隙水压力，对该模型的各个边界面施加相当的水压力，同时将模型边界、溶洞和掌子面设定为透水边界。

考虑施工扰动对溶腔和塑性区的影响，在实际的开挖模拟过程中，将开挖的步幅设定为2 m，采用全断面开挖，总共设置了28个开挖步骤。溶洞中心在隧道正上方，位于隧道纵向长度中点，即28 m处，也就是开挖步骤14。具体的隧道开挖如图2所示。

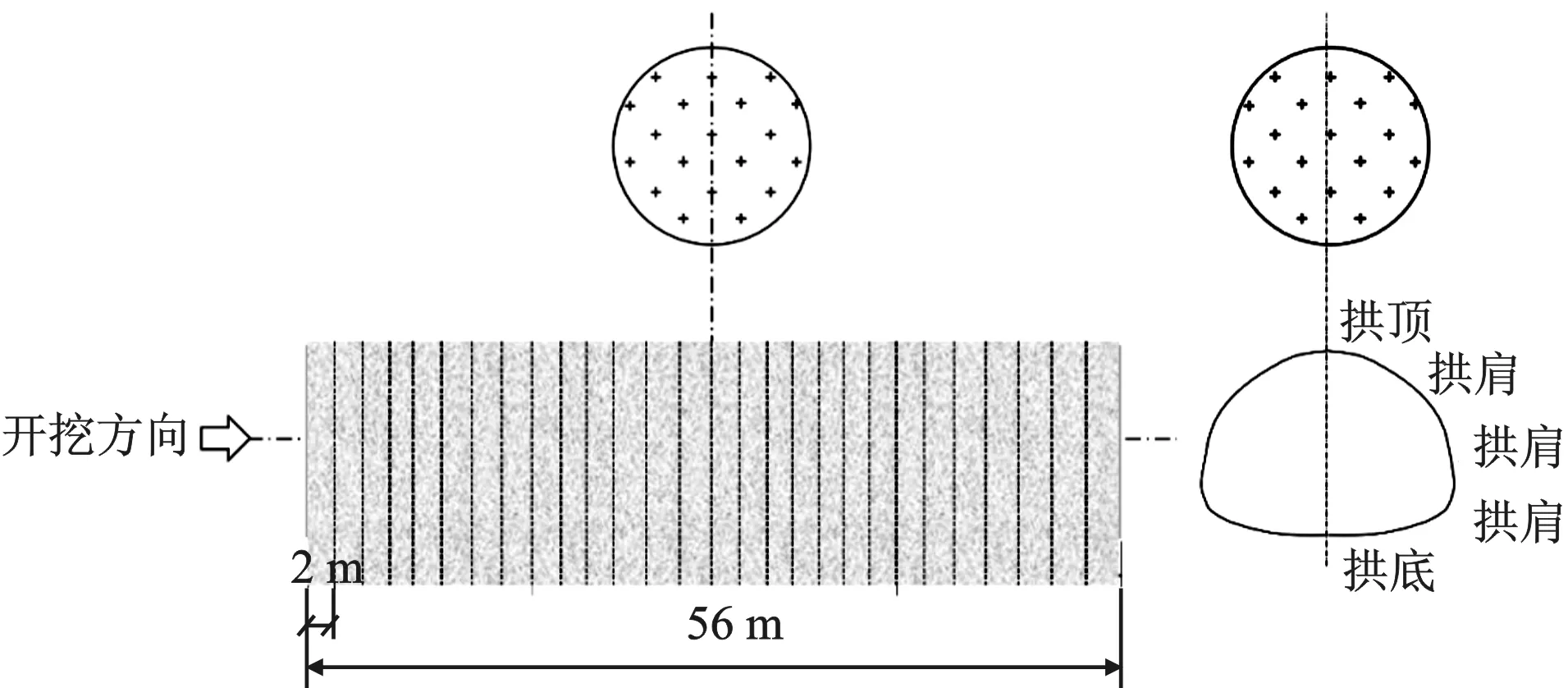
图2 隧道开挖示意

2.3 模型计算工况

为研究隧道埋深和溶洞大小对结构稳定性的影响，利用控制变量法，在研究其中一个因素变化时，另一个因素的取值保持不变，将2个因素分别划分为3个等级，即溶洞水压0.3、0.4、0.5 MPa，溶洞半径6、7、8 m，如表1所示。

2.4 模型参数选定

模型的材料参数取值见表2。按全断面法进行隧道开挖，由于表1中的计算工况较多，隧道三维模型的计算量较大，因此进行了隧道开挖初期支护设置，并进行二次衬砌设置，将隧道衬砌轮廓设定为不透水边界。

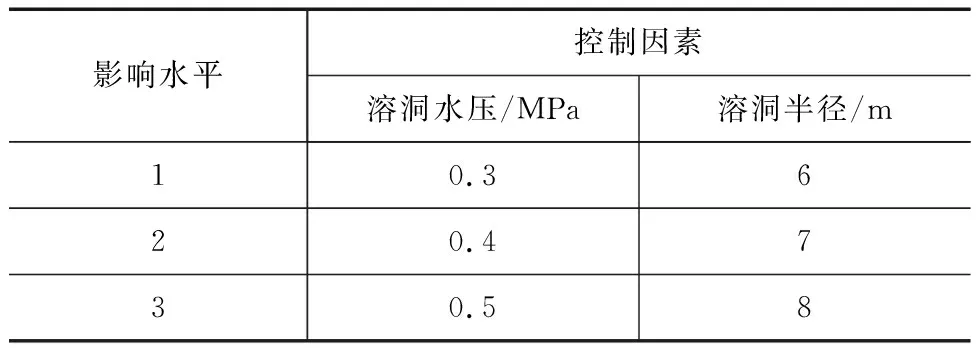
表1 模型计算工况

表2 模型材料参数

根据现场情况，将模型的地下水头统一为80 m，考虑渗流与流体的计算，模型中的流体取值为：水体积模量为2×109Pa，围岩渗透系数为4.92×10-10，围岩孔隙率为0.40。

3 计算结果分析

3.1 隧道围岩应力场分布特征

为分析溶洞水压对岩溶隧道围岩应力及塑性区的影响，选取溶洞半径R为6 m，开挖步骤15(已越过溶洞下方的隧道部分)，对其进行应力计算，绘制应力云图，如图3所示。

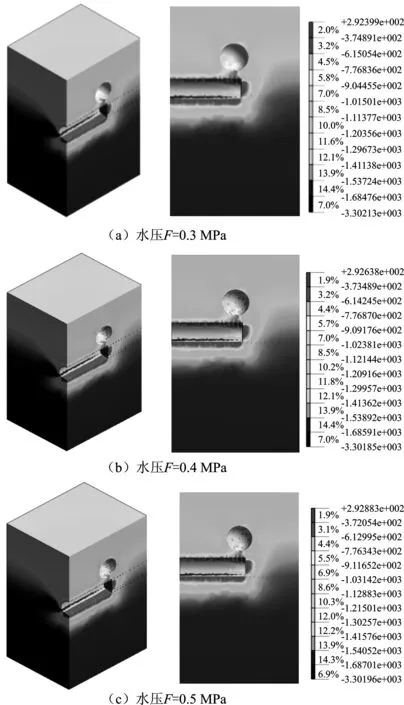
图3 不同水压充填溶洞的围岩最大主应力云图

由图3可知，围岩的最大主应力呈现左右对称特征。此时可以看出，溶洞水压对围岩应力的影响很小，不同溶洞水压的最大主应力几乎不变，但也略有差别；掌子面前方较小范围的围岩出现拉应力，掌子面表面应力释放较为明显，当溶洞水压为0.5 MPa时，最大拉应力为0.29 MPa。在拱脚部位出现应力集中现象，以压应力为主，最大为1.69 MPa，掌子面前方较近距离围岩以拉应力为主，距离隧道越远，应力越小，其表面围岩最大拉应力为0.29 MPa(溶洞水压为0.5 MPa)；沿着溶洞洞壁向外，最大主应力逐渐增大；溶洞水压越大，掌子面前方围岩及塑性区的最大主应力越大。

为分析隧道拱圈的应力特性，选择Z=-28 m的隧道横断面作为监测断面，选择拱顶、拱腰、边墙部位未开挖围岩作为分析对象，其随开挖步骤应力变化曲线如图4所示。

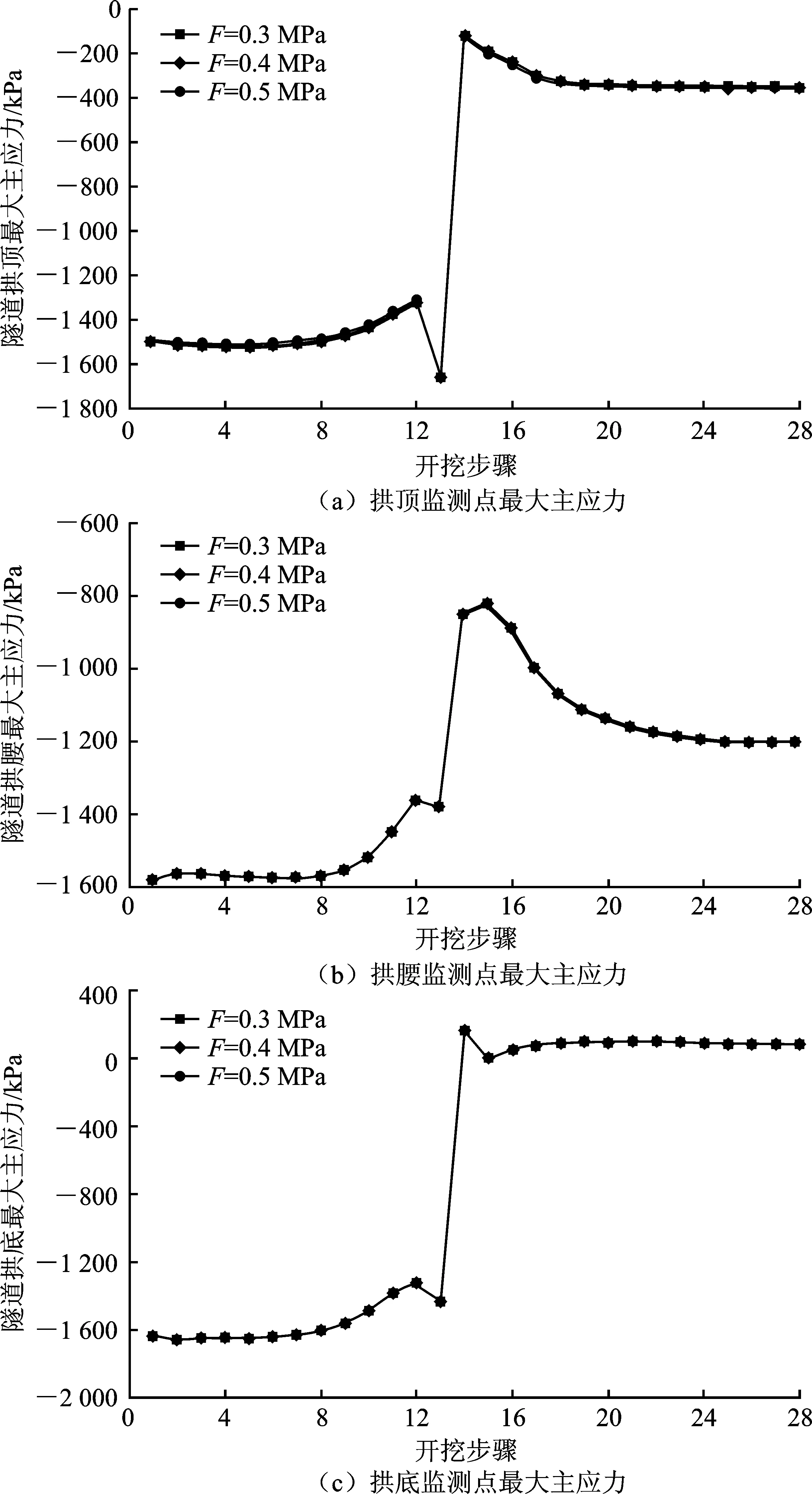
图4 隧道拱圈监测点的最大主应力随开挖变化曲线

从图4可以看出，在不同水压充填溶洞时，各个监测点的曲线几乎没有变化，即上覆溶洞的水压对隧道拱圈应力的影响不大。

3.2 隧道拱圈的位移变化特征

选取Z=-28 m为监测断面，对各监测点的位移变化情况进行计算，并绘制曲线，如图5所示。

图5 监测点的位移随开挖变化曲线(溶洞半径为6 m时)

由图5可知：拱顶部位随隧道开挖发生沉降，并逐渐增大，其中溶洞水压为0.5 MPa时沉降量最大，为12.72 mm；拱腰部位发生收敛，并逐渐增大，其中溶洞水压为0.5 MPa时收敛量最大，为2.97 mm；拱底部位发生隆起，并逐渐增大，其中溶洞水压为0.5 MPa时隆起量最大，为13.63 mm。

同时，随着溶洞充填水压的增大，监测点位移量也在变大。

3.3 围岩孔隙水压力特征

采用开挖步骤9断面(Z=-18 m)的计算云图，对不同水压充填溶洞的孔隙水压力进行总体分析。

模型设定了固定水位，在不同水压充填溶洞的影响下，孔隙水压力出现分层现象，在掌子面前方较短区域出现孔隙水压力低值圈，在掌子面前方较远区域出现孔隙水压力高值圈。从图6可以看出，溶洞水压对围岩孔隙水压的影响不大，不同水压溶洞时孔隙水压力的低值圈与高值圈也无太大差异。

为研究不同水压充填溶洞时，塑性区孔隙水压力随施工进度的变化规律，对各监测点孔隙水压力进行监测，绘制孔隙水压力及孔隙水压力变化速率曲线，如图7所示。

在相同溶洞半径、不同水压充填溶洞时，最危险开挖步骤并无变化，最小安全厚度也无变化。

4 结 语

本文建立了星子山隧道在不同溶洞水压下的数值模型，通过分析模拟结果，得出以下结论。

(1)围岩的最大主应力呈左右对称分布，水压对围岩压力的影响较小，但在拱脚仍会出现应力集中；掌子面前方围岩和塑性区最大主应力随着水压增大而增大，因此，在施工过程中需要加固和预防。

(2)不同水压充填溶洞时，围岩拱圈应力变化趋势一致，围岩拱圈位移增大，且拱底隆起量最大，拱顶沉降量次之，拱腰收敛量最小。最大拱底隆起量为13.63 mm。

(3)在相同溶洞半径、不同水压充填溶洞时，最危险开挖步骤和最小安全厚度基本没有受到影响，因此，在施工过程中可以不用考虑水压对施工进度的影响，优化施工管理。

图6 不同溶洞水压影响下的孔隙水压力云图

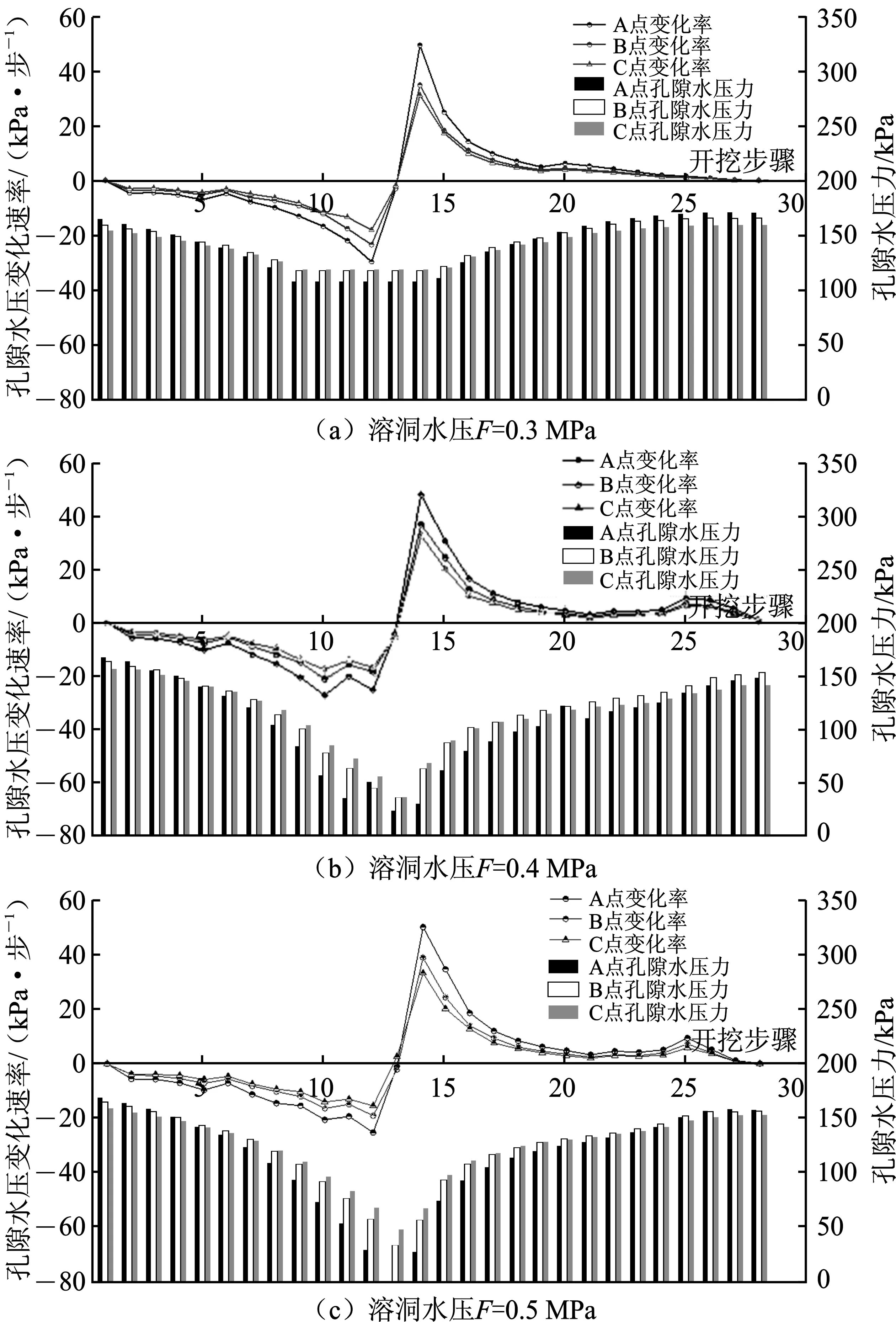
图7 塑性区监测点的孔隙水压力及速率随开挖变化曲线