改良千枚岩的无侧限抗压强度预测模型

王 鹏，邱 洲

(1.中交第二公路勘察设计研究院有限公司，湖北 武汉 430056； 2.中国交建东北区域总部，辽宁 沈阳 110100)

0 引 言

按照绿色公路的建设理念，公路路基应尽量做到填挖平衡，减少线外取弃土工程量。但风化千枚岩属于软岩，具有力学强度较低、水稳性能差、抗变形能力差等特点，路用性能较差，不宜直接填筑。中国铁路和高速公路的路基一般先进行填料改良处理后填筑[1-2]。

公路路基的变形和破坏主要是由于受到长期的降雨与暴晒反复作用，导致强度降低。因此无侧限抗压强度是反映软岩改良填料物理力学特性以及水稳定性的关键指标[3-5]，通常作为软岩改良填料填筑的控制指标。无侧限抗压强度一般通过室内试验测得，但受试验仪器设备、试验环境、人员误差等因素影响，对于多水平、多因素、多指标试验，传统的回归分析方法局限性明显。利用BP 神经网络强大的非线性映射能力，能够建立反映不同参数之间的映射关系的预测模型[6-9]。

1 BP神经网络模型

1.1 BP神经网络的基本原理

BP(Back Propagation)神经网络是一种按误差逆传播算法训练的多层前馈型神经网络，可以实现从输入到输出的任意非线性映射，是目前应用最广泛的神经网络模型之一。

典型的BP神经网络包括输入层、隐含层和输出层，各层间实行权连接。图1为典型的三层结构BP神经网络模型。

图1 BP神经网络模型

1.2 BP神经网络的训练过程

BP神经网络的训练包括前向计算和误差反向传播，通过两者的往复循环，不断修正网络神经元权值和阈值，最后使输出值的误差满足要求。

1.3 BP神经网络预测模型的实施步骤

1.3.1 依据正交试验理论确定训练样本

正交设计原理是依据正交性原则挑选试验范围内的代表点[10-12]。依据正交性原则安排试验方案可大大减少试验次数，并且具有均匀分散性和整齐可比性，非常适用于多因素、多水平试验。

1.3.2 确定神经网络结构

对于BP神经网络来说,网络的结构包括输入输出层单元数、隐含层数、隐含层单元数和隐含层、输出层神经元特性函数。输入输出层单元数由具体问题决定，隐含层数(至少为1)和隐含层单元数由用户确定。常用于选择最佳隐含层单元节点数的参考公式为

式中：n1为隐含层节点数；n为输入节点数；m为输出节点数；c为1～10之间的常数。

1.3.3 BP网络的训练与预测

对由正交试验理论获得的训练样本进行归一化处理，然后进行BP网络设计与训练，在一定收敛条件下获取相应的权值矩阵与阈值向量，得到训练好的神经网络模型。将预测样本参数代入前述模型中进行网络仿真，从而预测相应的参数。

1.3.4 试验验证

按照预测样本的试验参数条件进行室内试验，得到实测结果。比较预测值与实测值的相对误差，以此判断BP神经网络预测模型的可行性。

2 工程实例

2.1 填料的工程性质

以笔者参与勘察设计的陕南某山区高速公路为例，项目位于风化千枚岩分布区域(图2)，桥隧比接近60%，在隧道工程、路堑边坡的开挖过程中，产生大量风化千枚岩弃料。取样进行室内试验分析，得知主要矿物成分为石英与绢云母，基本物理指标如表1所示。

图2 风化千枚岩

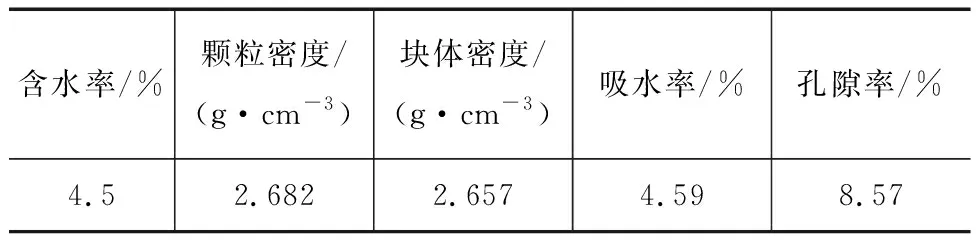
表1 风化千枚岩的基本物理指标

2.2 水泥的选取

选用P.C32.5水泥对风化千枚岩填料进行改良，其物理性能参数见表2。

表2 水泥的物理性能参数

2.3 训练样本的获取

无侧限抗压强度的主要影响因素为水泥掺量、压实度、龄期[13-19]。根据《公路土工试验规程》(JTG E40—2007)制备试件，进行无侧限抗压强度试验。选取水泥掺量、压实度和养护龄期3个主要影响因素，进行三因素四水平正交试验。其中水泥掺量(质量比)取2%、3%、4% 、5%四个水平，压实度取90%、93%、97%、99%四个水平，龄期取3 d、7 d、14 d、28 d四个水平，对16组试件进行无侧限抗压强度试验，见表3。

表3 神经网络输入样本

2.4 预测模型的建立

在表3的样本数据中，水泥掺量、压实度、龄期作为输入神经元，无侧限抗压强度值为输出神经元。由于样本数据差异较大，向量之间的数量级相差较大，为减少网络学习时间，加快收敛速度，提高预测精度，在网络训练之前先对样本数据进行处理，使其归一化至区间[-1,1]内。网络层间传递函数为tansig，训练函数为trainlm。根据BP神经网络原理，模型的输入神经元有3个，隐含层神经元个数应在3～12之间。为便于对比分析，选择3 种不同的网络结构(隐含层单元个数分别为3、7、9)，分别检验其网络性能。经过训练后发现，当隐含层神经元数为7时，误差相对较小，网络的性能最好。

核心代码如下。

[inputn,inputps]=mapminmax(input);

[outputn,outputps]=mapminmax(output);

net=newff(inputn, outputn,7);

net.trainParam.epochs=1000;

net.trainParam.lr=0.1;

net.trainParam.goal=0.0001;

net=train(net,inputn,outputn);

BPoutput=mapminmax(‘reverse’,an, outputps);

…

预测模型的拟合度如图3所示。

图3 预测模型拟合度

2.5 数据预测

为检验BP神经网络模型的预测性能，选取不同的水泥掺量、压实度、龄期进行无侧限抗压强度预测，预测样本数量占训练样本数量的25%，预测数据如表4所示。

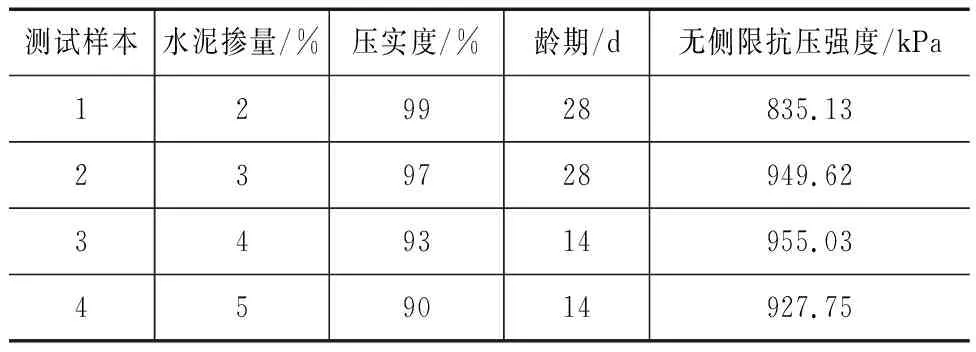
表4 BP神经网络预测数据

2.6 试验验证

按照测试样本中的水泥掺量、压实度、龄期条件，进行无侧限抗压强度测试，得到实际试验的无侧限抗压强度值，并与预测数据进行对比，如表5所示。

表5 预测结果与试验结果的误差比较

由表5可知, 无侧限抗压强度预测值与试验值的绝对误差为30.38 kPa，最大相对误差为3.10%，满足工程精度要求。结果表明，运用BP神经网络模型对改良风化千枚岩的无侧限抗压强度进行预测是可行的。

3 结 语

(1)将水泥掺量、压实度、龄期作为输入神经元，无侧限抗压强度作为输出神经元，建立BP神经网络预测模型，得出无侧限抗压强度预测值与试验值的绝对误差为30.38 kPa，最大相对误差为3.10%，满足工程精度要求。

(2)改良风化千枚岩的无侧限抗压强度主要受多种因素相互作用的影响，采用BP神经网络预测原理建立的无侧限抗压强度预测模型可以较好地映射其内在联系。该模型能够对不同水泥掺量、压实度、龄期的改良水泥填料进行强度预测，大大减少试样数量，节省大量人力、物力、财力、时间，为路基填筑提供了理论根据，对于路基设计与施工有重要的指导意义。

(3)BP神经网络模型的预测结果虽然与试验值存在误差，但是基本可以满足工程精度要求。因此，通过BP神经网络模型对改良土的无侧限抗压强度值进行预测是可行的。