自走式拾膜输送机构设计与试验
2020-10-19李卫敏王立强靳奉奎
付 磊,罗 昕,李卫敏,胡 斌,陈 永,王立强,靳奉奎
(石河子大学 机械电气工程学院,新疆 石河子 832000)
0 引言
地膜覆盖技术于20世纪70年代引入我国,由于其具有保墒、增温、除草、防虫、增产等功效,在农用生产上得到广泛应用[1-4]。我国多数地区使用的农膜厚度为0.006~0.008mm,残膜回收时由于地膜过薄导致老化破损严重,大量碎膜残留在农田中,给后续残膜回收带来困难[5-8]。我国实施的新标准规定农膜的最小厚度不小于0.01mm,新地膜标准的实施将大大提高地膜的可重复利用性和可回收性[9-10]。目前,我国残膜回收机常用的捡拾机构有耙齿式、伸缩杆式、链齿式等几种,大都结构复杂,需拖拉机另外提供动力驱动工作,能耗较高[10-12]。为此,针对一种自走式拾膜输送机构,不需另加额外动力,利用杆齿与土壤相互作用带动机构工作,对其进行了结构设计、受力分析和运动分析,并通过Box-Behnken试验设计建立了以拾膜率为响应值的回归模型,确定拾膜输送机构各参数对拾膜率的影响大小,获取参数最优值。
1 拾膜机构工作原理与结构设计
1.1 结构与工作原理
拾膜输送机构是残膜回收机具关键工作部件,主要由滚筒、滚筒端盖、曲轴及伸缩杆齿组组成,如图1所示。拾膜输送机构工作时由拖拉机牵引前行,工作深度由拖拉机三点悬挂装置调节。工作时,伸缩杆齿刺破残膜扎入土壤,杆齿与土壤相互作用,并在机具前进运动带动下使杆齿绕其末端转动,杆齿组绕曲轴转动并在滚筒接触带动滚筒转动;杆齿出土时带动残膜与土壤分离,残膜随着滚筒的转动输送至脱膜装置处进行脱膜。
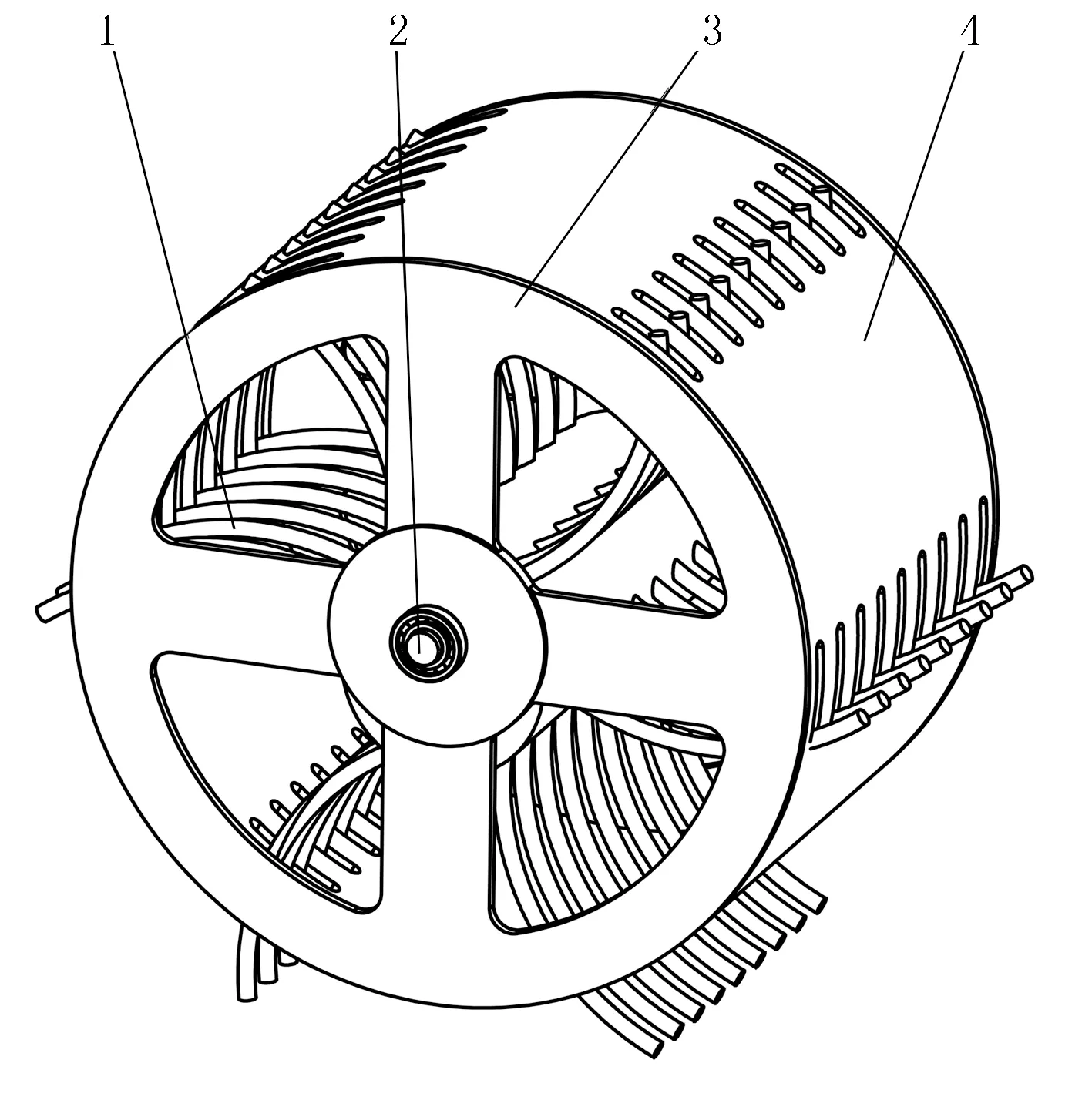
1.伸缩杆齿组 2.曲轴 3.滚筒端盖 4.滚筒图1 自走式拾膜输送机构Fig.1 Self-propelled film pickup and transport mechanism
1.2 结构设计
拾膜输送机构在捡拾残膜过程时,要求伸缩杆齿连续转动且不漏捡,前一个杆齿末端出土时应是下一个杆齿末端入土时。此时,杆齿转过角度θ,需要的时间为t。拾膜输送机构结构简图如图2所示。由图2得
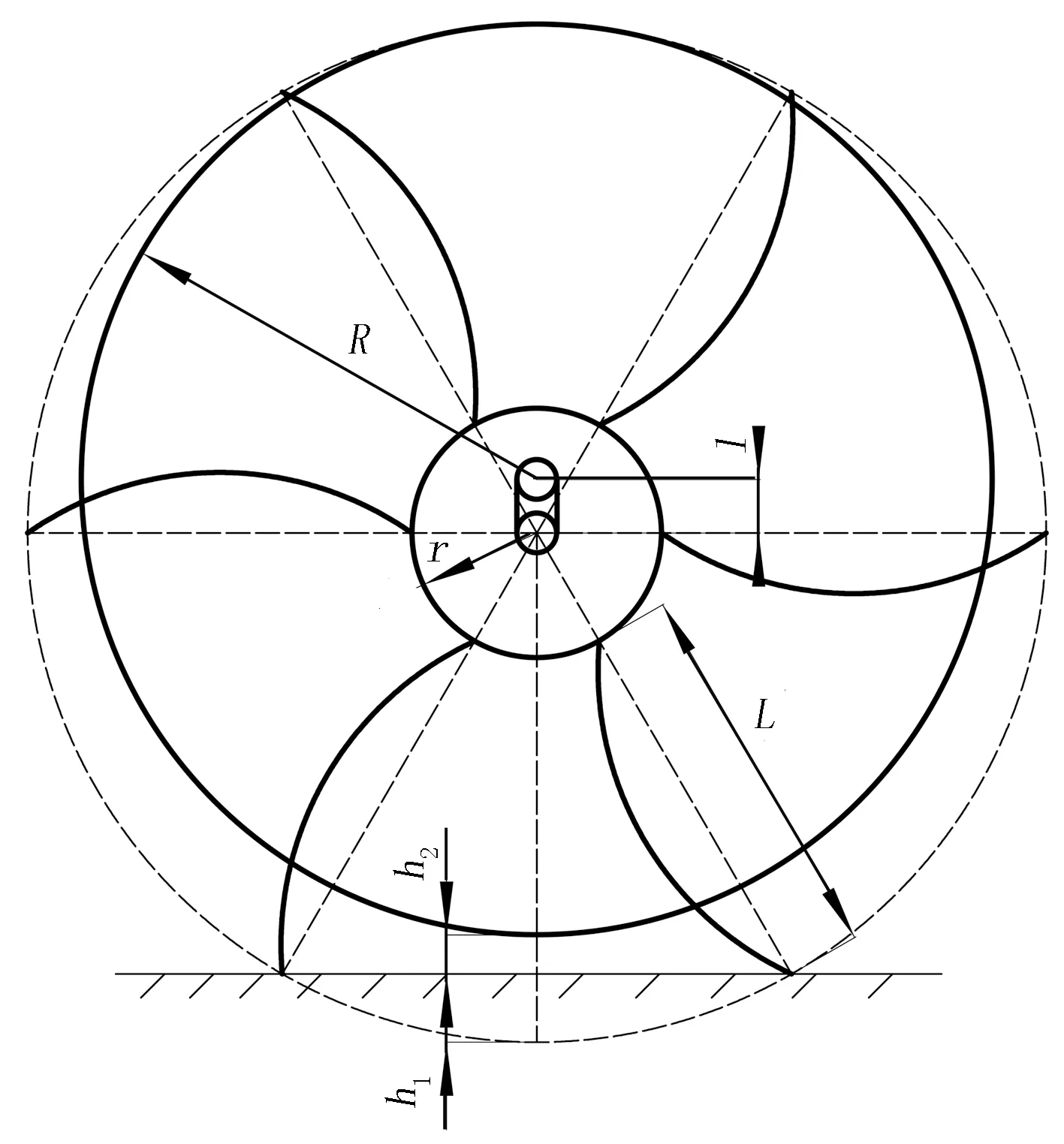
图2 拾膜输送机构结构设计简图Fig.2 Design sketch of film pickup and transport mechanism
R+l=L×cosθ+h1
R-l=L×cosθ-h2
vt=Ltanθ
h1=L(1-cosθ)
2θ=2π/z
式中R—滚筒半径;
l—偏心距;
L—杆齿长度;
h1—杆齿入土深度;
h2—滚筒与地面距离;
z—杆齿个数。
综上可以得出,只要机具的行走速度v、杆齿的入土深度h1、杆齿长度L及杆齿个数z确定,就可使机构具有连续运动和持续捡膜的功能。
2 拾膜机构运动分析与受力分析
2.1 运动分析
运动分析是为了寻找当机具稳定工作时伸缩杆齿的运动规律,以便确定拾膜输送机构的合理运动参数。拾膜输送机构运动分析如图3所示。图3中,拾膜输送机构从O1位置至O2位置为入土过程,O2位置至O3位置过程为出土过程。伸缩杆齿随机具的行走
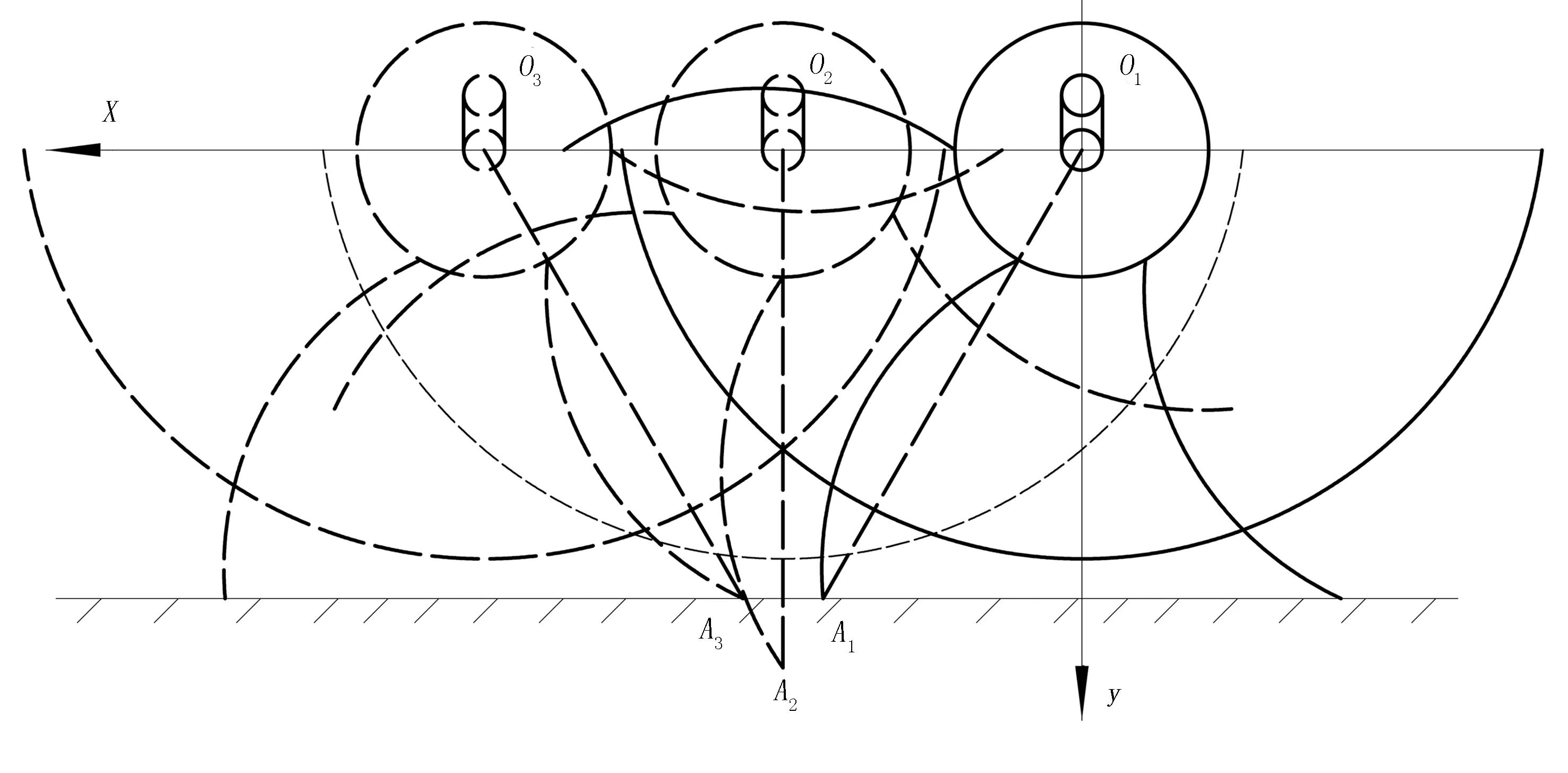
图3 拾膜输送机构运动分析Fig.3 Motion analysis of film pickup and transport mechanism
速度v一起移动,同时又以ω绕曲轴做转动。在工作过程中,伸缩杆齿与滚筒相对摆动角度经分析为14°。
当机构从位置O1至位置O2时,也就是杆齿末端从开始入土点A1至入土最低点A2的过程。假设伸缩杆齿入土过程的时间为t1,可得杆齿末端轨迹方程为
对以上方程组求导可得到杆齿末端速度和加速度方程组为
当机构从位置O2至位置O3时,也就是杆齿末端从入土最低点A2至出土点A3的过程。假设伸缩杆齿出土过程的时间为t2,可得杆齿末端轨迹方程为
求导可得到杆齿末端速度和加速度方程组为
式中v—机具前进速度;
φ—杆齿初始位置角;
L—杆齿长度;
ω—杆齿转动角速度。
根据工作过程可知:杆齿末端处于最低位A2(即机构位于O2位置)时,杆齿末端速度为0,此时v=Lω。
2.2 受力分析
机构在工作过程中的受力分析如图4所示。在杆齿入土时对杆齿进行受力分析目的是使杆齿易于刺破残膜并便于入土,杆齿在入土时刻杆齿受力为
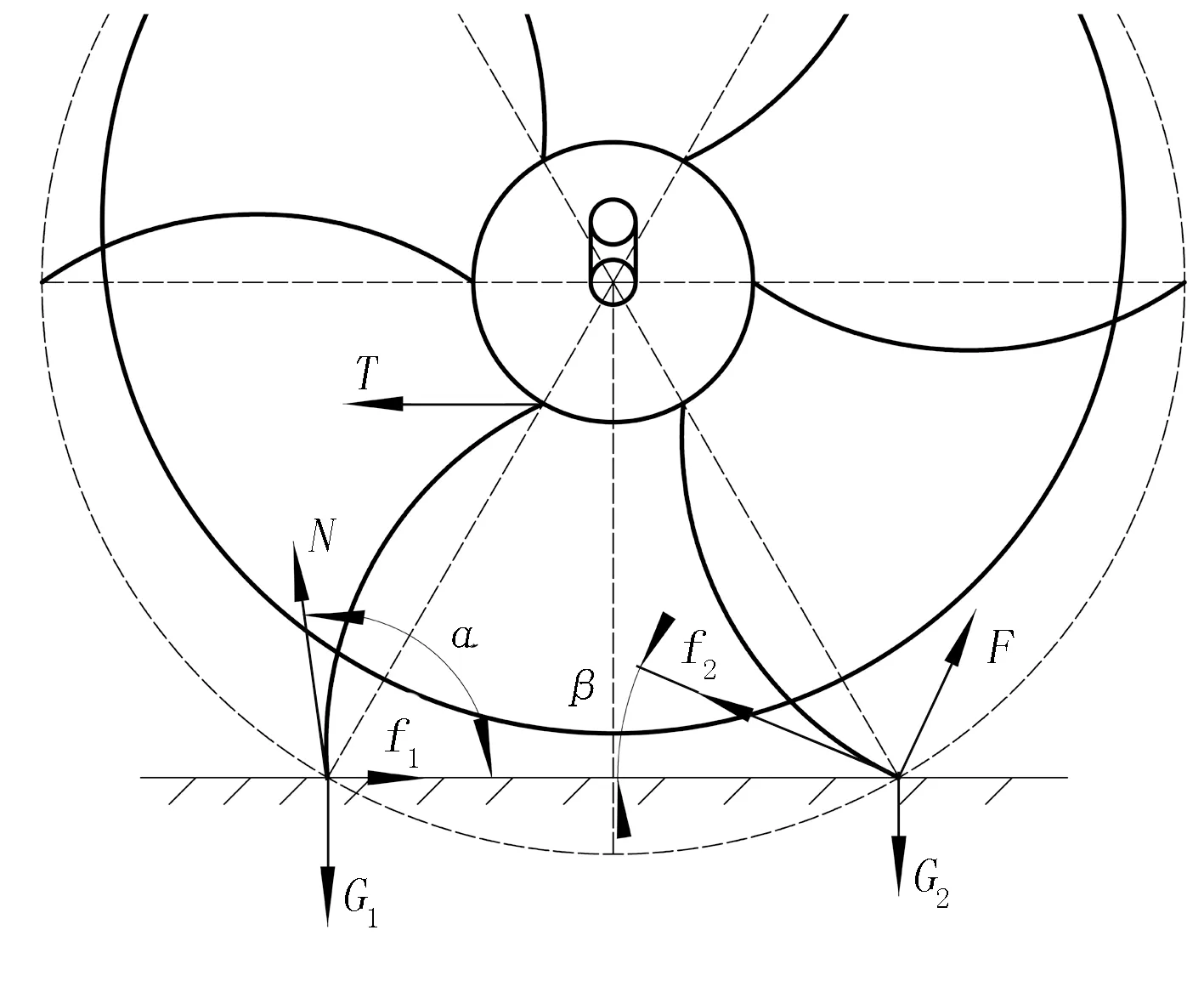
图4 拾膜输送机构受力分析Fig.4 Force analysis of film pickup and transport mechanism
在杆齿出土时对杆上残膜进行受力分析目的是防止残膜从杆齿脱落,杆齿在出土时杆齿上残膜所受力为
3 搭建试验台架与试验分析
为了验证理论分析的正确性和各参数因素水平对机构拾膜率的影响,对拾膜输送机构进行试验研究。由于田间试验研究复杂且周期较长,因此利用搭建试验台架模拟田间实际工作状态,探究各个参数因素对机构拾膜率的影响大小。试验在拾膜机构试验台上进行,试验土壤湿度为10%~20%。选取厚度为0.01mm农用新标准地膜,试验过程中称重选用精度为0.01g的电子秤。
3.1 试验评价指标
拾膜输送机构作业效果的主要评价指标是拾膜率,计算公式为
式中τ—拾膜机构的拾膜率;
m1—拾膜机构捡拾的地膜质量;
m2—拾膜机构未捡拾的地膜质量。
3.2 参数的选择及试验设计
通过对拾膜输送机构的的结构设计及运动分析,拟选定机具前进速度v、杆齿入土深度h1、杆齿出土角度β为试验因素,探究试验因素匹配变化对机构拾膜率的影响,确定机构工作时最优参数组合。进行台架试验时,保持所涉及的其他参数不变,如机构的其他尺寸、土壤的参数等均保持不变。根据理论分析和实际工作,初步选定参数因素取值范围为:机具前进速度v为0.6~1.0m/s,杆齿入土深度h1为80~120mm,杆齿出土角度β为20°~35°。根据Box-Behnken设计的响应曲面试验设计三因素三水平回归正交试验,试验方案包含17个试验点,有12个分析因子及5个零点估计误差。试验确定的因素水平表如表1所示,试验方案设计与试验结果如表2所示。

表1 试验因素与水平Table 1 Factors and levels of experiment

表2 试验方案与试验结果Table 2 Experimental scheme and results
3.3 试验结果分析及优化
3.3.1 回归模型建立与方差分析
运用Design-Expert 8软件对表2中的试验数据进行方差分析并建立回归模型,建立响应指标拾膜率对机具前进速度、杆齿入土深度、杆齿出土角度这3个因素的二次多元回归方程,即
Y=+90.35-0.91A+0.53B-0.71C+0.000AB-
0.11AC+0.088BC-5.67A2-3.69B2-4.33C2
其中,Y为拾膜率;A、B、C分别为机具前进速度、杆齿出土角度、杆齿入土深度因素编码值。
对回归方程进行方差分析,结果如表3所示。拾膜率回归模型的P<0.000 1,表明回归模型极其显著;失拟项P=0.864 7>0.05,表明回归方程的拟合度较高。因此,机具参数可使用该回归模型进行优化。

表3 回归模型方差分析Table 3 Variance analysis of regression model
因素P值的大小反应该因素参数对回归模型的影响大小。P<0.01表明因素参数对模型影响极其显著,P<0.05表明因素参数对回归模型影响显著[13]。分析表3可得:因素A、A2、B2、C2对回归模型的影响极其显著,因素B、C对回归模型的影响显著,因素AB、AC、BC对回归模型的影响不显著。各因素参数对回归模型影响大小从大到小依次为:机具前进速度﹥杆齿入土深度﹥杆齿出土角度。
三因素之间交互作用对拾膜率影响的响应曲面图如图5所示。分析图5可知:各因素对拾膜率的影响均很明显,且随着各因素参数值的增加,拾膜率均呈现出先增加后减小的趋势,因此存在各因素参数最优值。
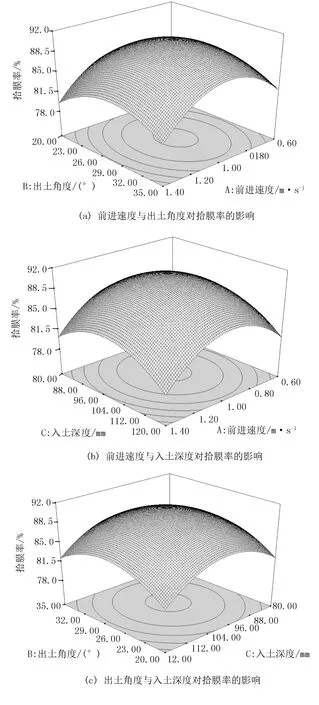
图5 因素交互作用对拾膜率的影响Fig.5 Effect of factor interaction on the film pickup rate
3.3.2 参数优化
运用Design-Expert中的Optimization-Numerical模块对拾膜率进行优化求解,得到拾膜输送机构最优工作参数为:机具前进速度为0.97m/s,杆齿出土角度为28.03°,杆齿入土深度为98.41mm,拾膜率为90.44%。
4 结论
1) 运用理论分析对拾膜输送机构进行结构设计、受力分析和运动分析,确定了对机具工作过程有影响的试验因素及范围。
2) 设计了三因素三水平试验,利用Design -Expert数据分析软件建立了机具工作参数(机具前进速度、杆齿出土角度、杆齿入土深度)对拾膜率的回归方程,确定了因素参数对拾膜率影响大小从大到小依次为:机具前进速度、杆齿入土深度、杆齿出土角度。
3) 运用Design-Expert软件对拾膜率进行最优求解,得到3个因素参数的最优组合:当机具前进速度为0.97 m/s、杆齿出土角度为28.03°、杆齿入土深度为98.41mm时,拾膜率最优。
