城市道路同向窄路段车速统计特性研究*

韩宝睿 宋婉璐 于晓妹 周 玉

(南京林业大学汽车与交通工程学院1) 南京 210037) (江苏交科能源科技发展有限公司2) 南京 210000)

0 引 言

同向窄机动车道是指部分路段存在车道宽度小于最小规范值(3.0 m)的具有同向双车道的城市道路，该类道路由于车道较窄，驾驶人在跟驰与超车或并行时的操作行为与较宽车道有一定差异，反映在交通流上也存在一定差异.关于窄车道的研究，以往主要从交叉口窄车道的通行能力效率及驾驶行为分析，山区窄车道的交通流特性分析等方面进行.Sapna[1]指出车道宽度是影响驾驶车速的限制因素，随着车道宽度的增加，地点车速方差及相邻车辆的速度差异都有所增加，合理设置道路车道宽度有利于限制车速波动.陈云等[2]以杭州市道路整治工程为例，通过驾驶人对窄车道的适应性问卷调查，定性验证了窄车道可以有效减少驾驶人的变道行为.韩宝睿等[3]通过建立仿真模型，得到了禁止超车的窄双车道的会车率与流量关系.目前，国内外对于车速与通行能力关联性研究主要以《道路通行能力手册》(2010)(以下简称HCM)为参考标准.但是，HCM中并未提及车道宽度在小于3 m时的通行能力折算系数.目前，国内北京、武汉、南京等城市部分道路，已经采用车道宽度小于3.0 m的机动车道[4].总体来说，车道宽度已呈现变窄趋势.

本文旨在通过对窄车道车辆车速的离散性进行分析，并将窄车道宽度与其自由流车速进行关联性研究，提出在窄车道条件下车速分布特征及车道宽度为2.8 m时的自由流速度折减系数，为窄车道道路断面建设提供理论基础的支持.

1 窄机动车道车速统计特性研究

1.1 观测路段情况概述

选取南京市富贵山分离式双向四车道道路为研究对象，分离式道路横断面可有效消除对向车辆的侧向影响.该道路全长1 425 m，其中隧道段长500 m，全线限速50 km/h.路段无监控设施，可以认为车速仅受到限速标志与道路条件影响.交通组成基本以小型客车为主(占总交通量的92%)，实施大货车全天限行措施，大型客车占总交通量的6%.该道路为封闭式道路，全段无出入口连接，外部环境干扰较小.经道路实勘，得到了其横断面见图1，其中机动车道宽度、路缘带宽度、侧分带宽度分别为2.8，0.3及1.3 m.

图1 富贵山分离式半幅横断面

1.2 地点车速调查结果统计分析

利用摄像法对富贵山窄车道早、晚高峰的地点车速数据进行采集，获得了578个有效样本，并通过SPSS的P-P,Q-Q正态性检验，证实其基本符合正态分布(即变量近似成为一条直线)，见表1和图2.

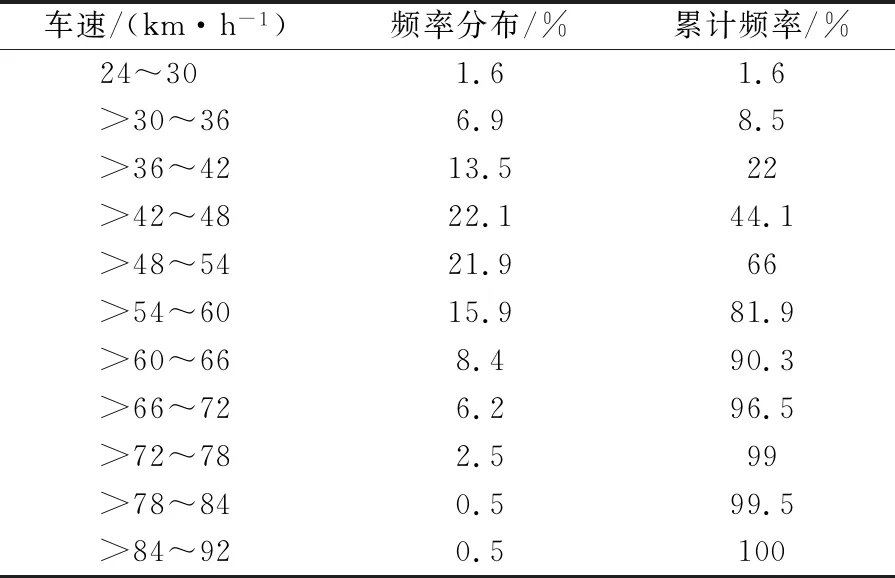
表1 车速频率分布表

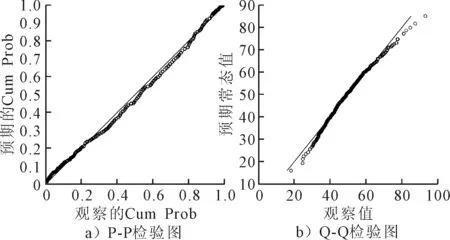
图2 车速分布正态检验

1.3 窄道与标准车道车速离散性对比分析

为了比较车道宽度为2.8 m的窄四车道特有的车速离散性特征，另外选取了南京市花园路、御道街及板仓街(双向四车道段)三条城市双向四车道，其车道分别宽度为(3.0，3.5及3.75 m)，对其地点车速进行观测统计，见表2.为了排除时间因素对实验结果的影响，调查时间与富贵山窄道地点车速调查时间一致.

表2 不同车道宽度地点车速特征值

引入离散系数概念，即用标准偏差与平均值的比值作为离散性分析的统计量，消除平均数不同对离散程度的比较影响[5].

经调查，富贵山窄道的高峰小时交通量与其他道路交通量的最大相对差值仅为14%，平均每5 min的相对差值仅为1.17%，在一定程度上，交通量的差异没有对车速起到较大干扰.表中窄车道的车速极差均高于其他道路水平，但是其离散系数却呈现较低水平.这说明，虽然窄车道不能对所有驾驶人的行车车速起到约束作用，但是对于大部分驾驶人(特别是处于跟车状态的车辆车速)能够起到较为明显的约束效果，直观数据表现为车辆车速离散程度较低，车速分布较为集中.对于窄车道，由于道路宽度限制，实施换道行为的难度增加，大部分车辆仍会选择跟驰行驶，形成有秩序的排队车流状态，从而车速分布更加均匀.

2 窄车道自由流车速折减系数的拟合与验证

HCM关于自由流车速的车道宽度修正值仅涉及到车道宽度在3.0～3.6 m的情况.由于土地资源、地形地势等原因限制，我国仍存在部分宽度小于3.0 m的道路，为了使得该手册能够更好地适用于我国道路，本文进行了车道宽度为2.8 m时的修正值分析.

2.1 基于统计学原理的实际自由流速度确定

1) 自由流车速数据的采集 为了尽可能保证录像法采集的车速样本处于自由流状态，仅选取调查断面上10 s检测周期仅有1辆车通过且车辆的空间占有率<12%(道路长度约为40 m)的数据作为分析对象[6-7].以2.5 km/h为组距，得到了121组自由流车速值.利用Grubbs[8]检验有效数据经计算，得到有效数据118组，无效数据3组.其频率统计图见图3.

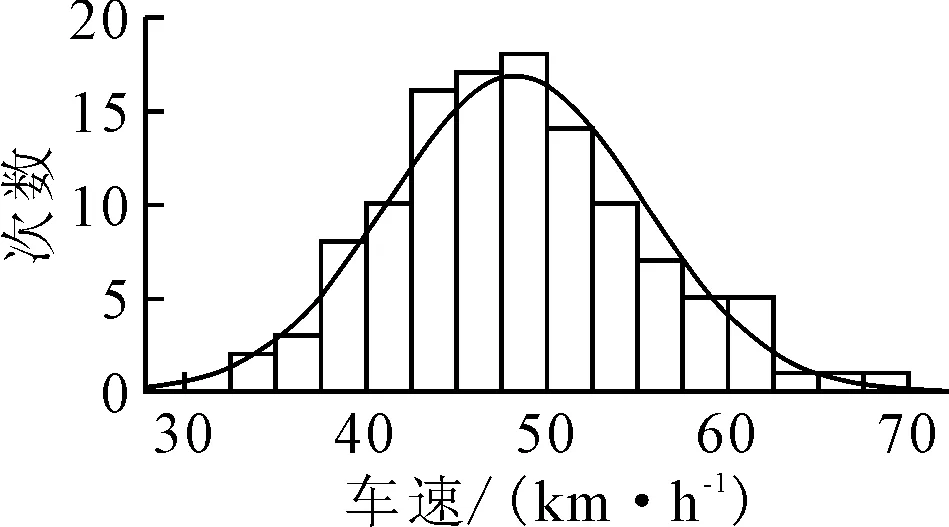
图3 自由流车速频率分布统计图

利用SPSS计算自由流车速频数分布直方图对应的正态分布曲线特征值，得到了窄四车道自由流车速的正态分布特征值：μ(期望)=48.28 km/h，σ(标准差)=7.004 km/h.

2) 正态分布检验 正态分布检验采用Kolmogorov-Smirnov法进行检验，如果相伴概率小于等于显著性水平α，则拒绝原假设H0，认为样本来自的总体与指定的水平分布有显著性差异；如果相伴概率值大于显著性水平α，则不能拒绝原假设H0，认为样本与指定的分布无显著性差异[9].

依据上述水平，对自由流车速进行K-S正态性检验，并设定显著性水平为0.05.得到其Sig(相伴概率值)=0.649>0.05，表示样本数据接受原假设，符合正态性检验，见表3.

表3 Levene方差齐次性检验表

3) 稳定性分析 为了研究在不同日期的自由流车速是否会有差异，本次研究采集四个不同日期、星期的样本车速进行上述过程的正态分布曲线绘制，并计算出其μ与σ，采用Levene方差齐次性检验对不同日期的期望自由流速度进行方差分析.其中显著性水平设置为0.05.

计算得显著性水平0.936>0.05,表明不同日期下的车速方差并无显著性差异，这说明在不同日期下得到的自由流车速是稳定的[10]，见表4.

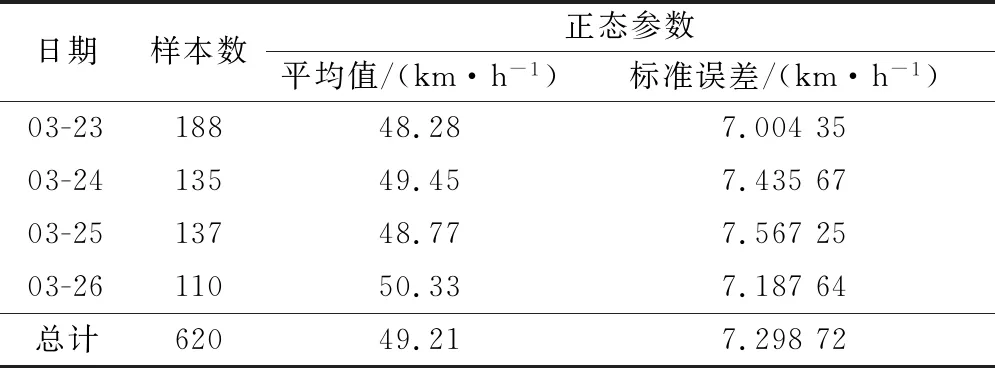
表4 自由流车速稳定性分析表

2.2 窄车道理论自由流折减系数的分析

1) 理论车道宽度的自由流修正系数 通过对已有的HCM中不同车道宽度对应的自由流速度减少值进行不同函数的拟合分析，得到其误差平方和与其确定系数关系见表5.

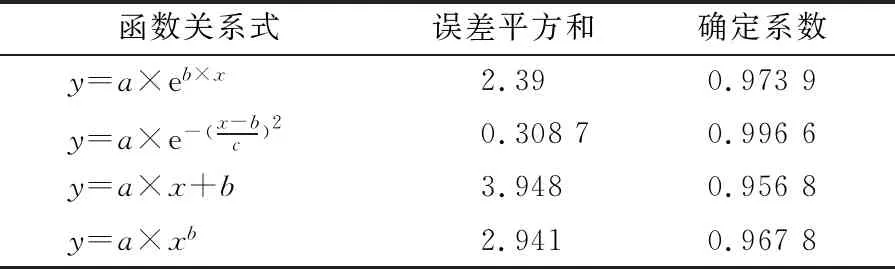
表5 多种函数拟合参数值对比

经过比较高斯(Gsussian)函数的误差平方和(SSE)接近于0，确定系数(R2)=0.996 6接近1，表明拟合度最好，故车道宽度与其折减系数呈现高斯函数递减关系，见图4.

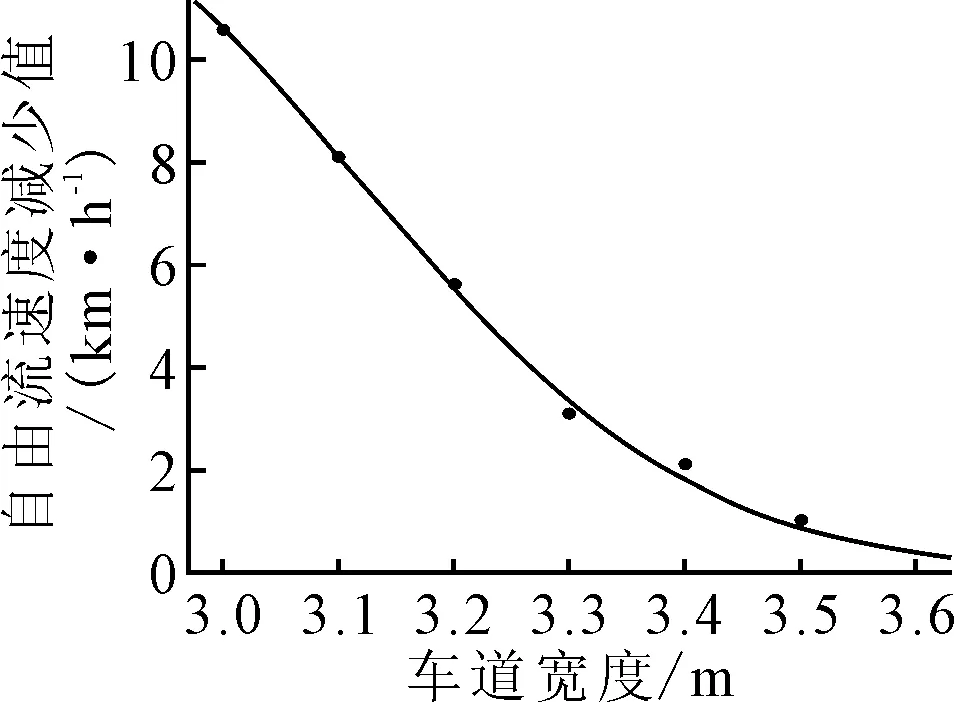
图4 车道宽度-自由流车速折减的Gaussian函数曲线

表达式为

y=12.82×e-(x-2.819)/0.415 5)2

(1)

当车道宽度为2.8 m时，其对应的自由流速度减少值应为12.79 km/h.

2) 计算理论自由流速度 HCM中指出，基础自由流速度(BFFS)为

FFS=BFFS-fLW-fLC-fM-fA

(2)

式中：BFFS为基础自由流速度，km/h；FFS为自由流速度估计值；fLW为车道宽度修正系数；fLC为侧向净宽修正系数；fM为中央带类型修正系数；fA为入口点修正系数.

①基础自由流速度 速度限制是自由流速度的一个重要影响因素[11].HCM中指出，在理想条件下的多车道道路的自由流速度，当速度限制为50～55 km/h，大约高出限速14 km/h;65～70 km/h时，大约高于限速11 km/h；80～90 km/h，大约高于限速8 km/h.

经调查显示，富贵山窄四车道限制速度为50 km/h，故其基础自由流速度约为64 km/h.

②车道宽度修正系数 据上述高斯函数自由流速度折减系数拟合公式，窄四车道在车道宽度为2.8 m时，其自由流折减系数为12.79 km/h.

③侧向净空修正系数 HCM中列出了因路旁或中央带固定障碍物的侧向净宽造成的自由流速度下降.其中，侧向净宽包括左侧向净空与右侧向净空的自由流速度折减.通过富贵山道路条件调查可知，左侧平均侧向净空为0.8 m，右侧平均侧向净空平均为1 m.HCM指出，当总侧向净空为1.8 m时，其自由流速度减少值为2.1 km/h.

④中央分隔带类型及出入口密度修正系数 本次实验区域选于分离式道路，已进行空间交通分隔，故不用考虑中央带类型.经查HCM得当道路设有中央分隔带，其自由流速度折减系数为0 km/h.

HCM中提出，在有分隔带的道路，道路出入口密度由行进方向右侧出入口(也就是交叉口和进出支路)的总数除以路段总长度(以km计)来决定.富贵山道路为封闭道路，故出口密度修正值为0 km/h.

上述修正系数确定后，通过式(2)可计算得在车道宽度为2.8 m时的理论自由流速度折减系数为49.11 km/h.

2.3 车道宽度修正系数显著性检验

显著性检验是事先对变量的参数或分布形式做出假设然后利用样本信息来判断这个假设(备择假设)是否合理，即判断总体的真实情况与原假设是否有显著性差异[12].本次显著性检验采用单总体t检验方式，其统计量为

(3)

建立原假设H0：λ(理论自由流车速)=49.11，及备择假设H1：λ≠49.11.选择双侧检验，并设置显著性水平为0.01，计算得t=0.251 6.判断：当显著性水平取0.01时临界值t(3)0.01=5.841>0.251 6，故接受原假设H0.表示理论值49.11可代替窄四车道平均自由流车速水平，即车道宽度在2.8 m时的自由流折减系数12.79是通过验证的.

3 结 束 语

运用SPSS、Matlab等软件，通过对窄车道与标准车道的车速数据进行离散性分析，证实在交通量基本呈同一水平时，窄车道的车速离散系数最低，车速分布最为集中，说明窄车道对车速有明显的约束作用.

通过对窄道自由流车速总样本进行统计，对样本数据进行了K-S正态检验及稳定性分析，获得了具备代表性的自由流车速值.并基于HCM原有的车道宽度(3.0～3.6 m)与其自由流折减系数规律，建立了车道宽度—自由流速度折减的高斯函数曲线.从而得到了当车道宽度为2.8 m，有中央分隔带(或者分离式道路不考虑中央分隔带)，总侧向净空为1.8 m，路段中无出入口影响的路段条件，其自由流折减系数为12.79 km/h.并通过了与实测自由流车速特征值的显著性分析，进一步验证了结果的准确性.本文已经提出了一套方法，如需其他窄车道宽度或者道路横断面条件的自由流折减系数，可结合已得到的高斯函数模型及HCM中不同道路条件的修正系数计算即可.

以上结论均证实了，在窄道条件下，能够约束驾驶人行车车速，从而使车速分布更加均匀，使道路交通更加安全、有序.本文不足之处是，在车速离散性研究方面，用于对比的道路案例较少，在自由流车速折减系数方面，缺少不同侧向净空的研究分析，后续工作将对此进行深入研究.