优化降雨因子分量的岩质边坡变形预测模型

单 郸，陈 辰，沈明毅，陈建康，裴 亮

(1.四川大学水利水电学院，成都 610065；2.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065)

0 引 言

岩质高边坡是自然历史发展的产物，具有强烈的不均匀性、各向异性和非连续性。这一特点致使岩质高边坡几乎成为影响和制约重大工程建设的首要工程地质问题[1]。1963年意大利瓦伊昂拱坝的失事也警示后人在工程前期论证中应重视库首天然高边坡的稳定。外界环境因素如施工开挖扰动、第一次蓄水、卸荷风化、降雨等作用均会劣化边坡岩体的性状。因此，对天然高边坡的预测预警成为水利水电工程安全监测的一大重要课题。

目前水电工程天然高边坡的失稳预测统计模型理论和方法研究相对比较成熟，除传统的多元线性回归分析和逐步回归分析外，还吸收了现代科学理论中的新理论以及工程经验中的新成果[2-7]。国内外研究学者针对高边坡安全监测统计回归方法进行了有益的探索和创新[8-10]。郑东健、顾冲时等[11]结合融合回归和递推模型的优点，建立具有时变特性边坡变形的统计回归预测模型，该方法提高了模型预测的精度。李聪[12]在弹性理论假定下推导流变、卸荷回弹因子表达式，并考虑降雨、爆破因子的影响，提出了考虑变形机制的边坡稳定统计回归模型。秦栋[13]将经济学领域空间计量学理论应用于水库边坡的变形预测，从时间和空间两个维度来探讨相邻边坡外观变形的关联性，运用某电站高边坡实测变形资料对空间自回归模型在高边坡变形预测的适用性进行研究。Ayalew[14]利用Logistic回归研究出有无滑坡发生(因变量)与坡角、岩性、基岩边坡关系、高程等独立参数之间的最佳拟合函数。各种方法均有其优点和局限性，但都无法满足天然高边坡长期监测的预警需求。通常情况下研究者根据自己的主观臆断，“先入为主”的选用传统降雨分量模型，而并未考虑到降雨滞后性造成的拟合缺陷。

本文针对边坡变形的4个影响因子，考虑降雨滞后性建立天然高边坡变形统计回归模型，结合国内某已建砾石土心墙堆石坝库首右岸岩质边坡拉裂体变形特性，对近期边坡拉裂体变形趋势进行预测拟合，分析比较各种模型预测精度，并得出适用于本工程的回归预测模型。

1 优化降雨因子的边坡变形预测模型构建

边坡的变形是在其自身重力、岩体蠕变等内部因素和水位、温度、降雨等外部环境因素综合作用下产生的结果。水位、温度一般呈周期变化，其对边坡变形的影响亦呈周期性变化，而在自重、材料蠕变等内外因素长期作用下边坡产生的变形则表现为随时间推移而逐渐增长的不可逆变形。因此，本文以统计回归方法构建岩质边坡拉裂体变形回归统计模型[11,15]，即：

Y(t)=F1[W(t)]+F2[θ(t)]+F3[H(t)]+F4[T(t)]+C

(1)

式中：Y(t)为边坡变形监测值在时间t的统计估计值；F1[W(t)]为边坡变形的降雨分量；F2[θ(t)]为边坡变形的时效分量；F3[H(t)]为边坡变形的水位分量；F4[T(t)]为边坡变形的温度分量；C为待定常数项。

1.1 降雨因子

降雨是影响边坡水动力条件以及变形的重要因素。降雨对岩质边坡的影响可分为两个阶段：第一阶段由于初期降雨强度小于岩体的渗透性，岩体以及裂隙的含水率增大，上覆岩体重度增加；第二阶段当岩体及裂隙含水率达到饱和状态时，岩体力学性质改变，抗剪强度、基质吸力、内聚力在后期持续降雨的作用下均有所降低，此阶段降雨主要以积水或地表径流的形式存在于岩质边坡表层[16]。在不同的降雨类型作用下边坡产生不同的破坏形式，针对不同的破坏形式往往采用不同的降雨量值进行预测分析。在低强度长历时降雨条件下，一般采用累积雨量分析边坡的滑动型破坏，而对于高强度降雨产生的流滑冲蚀破坏，一般采用时雨量进行分析[17]。

由于前期降雨是诱发滑坡发生的主要原因，在实际工程分析中，通常引入Crozier提出的有效降雨量公式[10]，来构建降雨因子模型，见式(2)：

(2)

式中：Pa为有效降雨量；K为降雨衰减系数；WL(ti) (i= 0, 1, 2,…,n)分别表示为滑坡当日、前1 d、前2 d、…、前nd降雨量。

一般情况下，考虑边坡变形滞后于降雨入渗的特征，降雨衰减系数K取1，并选取不同时段的平均降雨作为降雨因子，构建降雨模型，可见式(3)：

(3)

式中，WL(ti) (i= 0, 1, 2, 5, 10, 15, 20, 25, 30)分别表示变形观测日当天、前1、2、5、10、15、20、25、30 d各时段的平均降雨量；qi为待定回归系数。

谈小龙[18]针对传统降雨模型忽略时间远近对高边坡变形的影响，提出以0.8的降雨衰减系数折减并累计求和的思想，建立降雨模型，见式(4)：

(4)

优化降雨因子的关键是合理选取前期降雨衰减系数，而降雨衰减系数K的取值受相关地区的地质特征和灾害特点的制约，并与当地滑坡是否发生和滑坡发生数量的相关关系所决定[10]。因此结合岩质边坡降雨入渗特点，在构建变形预测模型时，降雨衰减系数K取经验值0.8会产生前期降雨量折减过大的干扰。为进一步分析岩质边坡变形规律，提高岩质边坡变形预测的准确性，本文从降雨型滑坡发生概率的Logistic回归模型[8,10]中引入待定指数函数exp(q0)来拟合不同时间间隔下的前期降雨衰减系数，即：

(5)

采用以上3种降雨因子函数，通过对岩质边坡拉裂体变形统计回归比较分析，说明优化降雨因子函数的适用性。

1.2 时效因子

时效分量反映的是一种随时间发展不可逆的变化。岩质边坡在自重、库水位水压等长期荷载作用下，会因岩体的劣化、破碎而导致岩质边坡变形量随时间的推移而递增。同时，岩体的蠕变、结构本身的节理裂隙及其他软弱构造在水压作用下发生的变形，以及库水位升降等循环荷载引起的不可逆变形亦随着大坝运行期年限的增加而递增，形成时效变形分量。考虑到其变形的非线性特点，采用工程中常用的线性和非线性的组合方式[19]，即：

F2[θ(t)]=a1θ+a2lnθ

(6)

式中：θ=ti/100，ti为观测时刻距初始时刻的天数；ai为待定回归系数。

1.3 水位因子

水库蓄水后，边坡任意点由于水压引起的变形一般与水位或水深的1～3次方有关。因此，水位分量的数学模型[20]形式可按以下函数构造：

(7)

式中：H1(t)为变形观测日的平均水位；H(t0)为基准水位；bj为待定回归系数。

1.4 温度因子

温度对边坡变形的作用一般仅对表层土体有影响，因此应对回归模型中温度因子做一定简化，假设各年的温度分量呈相同的年周期变化，那么温度分量的影响可表达成如下形式[19]：

F4[T(t)]=αcos(G+φ)+βcos(2G+θ)

(8)

式中：φ和θ为未知相位角，对其展开可得：

F4[T(t)]=α[cosGcosφ-sinGsinφ]+β[cos(2G)cosθ-

sin(2G)sinθ]=c1sinG+c2cosG+c3sin2G+c4cosGsinG

(9)

式中：G= 2 πti/365；ti为观测时刻距初始时刻的天数；ci为待定回归系数。

2 工程应用

2.1 工程概况

某电站右岸拉裂变形体位于坝轴线上游右侧约780 m处库首岸坡，由于低线公路硐室大爆破以及路堑边坡严重超挖的扰动，致使拉裂变形体坡体松弛变形，表部松散体失稳[21]，示意图如图 1。2003年2月首次在拉裂变形体后缘陡缓交界处覆盖层内发现裂缝，其后缘裂缝呈雁列状展布，分布于高程1 050～1 090 m位置，总体延伸方向为N29°E，发育长度近150 m，最大错距25 cm，张开约0.5～2 cm，最大张开10 cm。并在拉裂变形体中下部Ⅱ区浅表层中出现了滑塌变形，随后发生由下至上渐进式后退解体破坏，在坡体上形成了3个较大的滑塌槽。其中上游侧滑塌槽发展最快，于2003年5月后缘扩展至高程850 m附近，其后不断滑塌，最高发展到高程1 000 m左右。作为典型的拉裂变形体，其上布置了观测墩、锚筋束、锚索测力计等监测仪器实时评估边坡的安全性态。

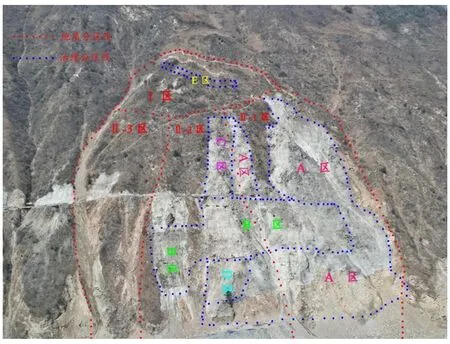
图1 拉裂变形体示意图Fig.1 Schematic diagram of tension crack body

2.2 优化降雨因子适用性分析

基于拉裂变形体拥有较长的安全监测序列，选取2010年4月20日至2017年12月31日作为观测时段，按式(1)建立拉裂体变形统计回归模型。参考库水位、温度的滞后性影响，降雨因子的滞后性以30 d为宜，选用不同时段的平均降雨量作为降雨因子，综合比较各降雨因子函数的拟合精度。

某电站库首右岸拉裂体在高程875 m马道层区域、高程975 m区域、高程1 030 m区域和高程1 100 m区域内布设21个变形观测墩，如图2。其中TP9～TP12 4个测点因水淹而停测。为掌握拉裂变形体的整体变形规律，选取拉裂体不同高程的六个典型测点进行统计回归分析，分别将降雨函数Ⅰ式(3)、降雨函数Ⅱ式(4)和降雨函数Ⅲ式(5)带入式(1)中，得到不同降雨函数下的各测点回归复相关系数，其计算公式见式(10)，计算结果见表1。

(10)

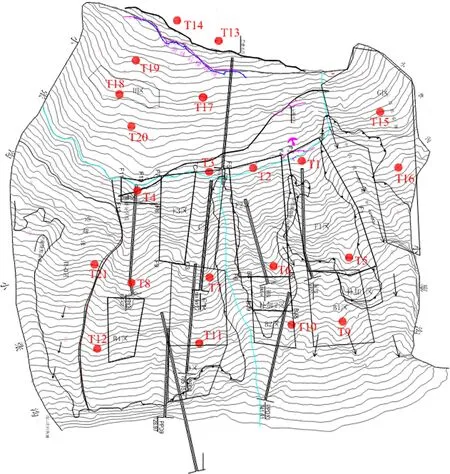
图2 拉裂变形体外观变形监测布置图Fig.2 Layout diagram for monitoring the appearance deformation of the tension crack body

表1 3种降雨分量函数回归复相关系数表Tab.1 Regression multiphase relation table of three rainfall factor functions

从总体上看，3种模型的回归拟合效果较为理想，回归复相关系数较高。降雨函数Ⅰ作为边坡工程中应用最广泛的降雨分量模型，形式简洁明了物理意义明确，但应用于实际工程中，该模型忽略了降雨时间远近对边坡的影响，认为前5 d的降雨与前30 d的降雨对边坡变形的影响程度相同。若考虑降雨滞后效应，往往近期的降雨对边坡的安全稳定影响更加显著。因此，考虑降雨发生时间远近对边坡的影响程度进行折减的降雨函数Ⅱ、降雨函数Ⅲ的回归复相关系数较降雨函数Ⅰ有所提高。此外，通过降雨函数Ⅱ与降雨函数Ⅲ关于前1～30 d降雨量折减系数的对比(表 2)可知，降雨函数Ⅱ对前期降雨量的折减程度过大，前3 d降雨的折减系数为0.64，前五天降雨的折减系数仅为0.41，这与一周内降雨对边坡影响较大的结论相矛盾。以降雨函数Ⅲ构建的统计回归模型在一定程度上解决了降雨函数Ⅱ前一周内折减系数过大的问题，更符合本工程的实际情况。

表2 降雨函数Ⅱ与降雨函数Ⅲ折减系数对比表Tab.2 Comparison of reduction coefficient between rainfall function Ⅱ and rainfall function Ⅲ

以拉裂变形体高程975 m区域内T4观测墩和高程1 030 m区域内T19观测墩为例，经拟合(见图3～图5)表明：①回归方程效果良好，回归精度均有所提高。T4、T19纵向位移回归复相关系数均提升0.001，竖向位移回归复相关系数最大提升0.02。②能够反映各测点的变形规律。T4沿临空面方向位移缓慢，且量值趋于收敛，符合该区域经加固处理后基本处于稳定状态的事实。而拉裂体1 030 m高程后缘开裂部位T19测点的回归表明，其向坡外变形以及沉降变形一直呈发展趋势，尚未收敛。③优化后的降雨折减系数对近一周内的降雨权重分配更为合理。综上所述，引入降雨函数III的统计回归模型更能反映降雨对边坡拉裂体变形的影响，从而有助于后续边坡变形的预测。

图3 T4观测墩纵向位移、竖向位移实测值与回归拟合值Fig.3 T4 observation pier longitudinal displacement, vertical displacement measured value and regression fitting value

图4 T19观测墩纵向位移、竖向位移实测值与回归拟合值Fig.4 T19 observation pier longitudinal displacement, vertical displacement measured value and regression fitting value

图5 降雨折减系数随时间变化关系图Fig.5 Relation diagram of rainfall reduction coefficient with time

3 结 论

本文依托某电站库首右岸边坡拉裂体工程，根据其近7年的边坡变形监测数据，对不同降雨因子分量与边坡变形的关系开展了统计回归研究，提出用待定指数函数代替单一降雨衰减系数的降雨因子分量，建立了考虑降雨折减的边坡拉裂体变形预测模型。具体成果如下。

(1) 选取降雨、时效、水位和温度4个影响因子，建立岩质边坡拉裂体变形预测统计回归模型。结合岩质边坡降雨入渗特点，提出了考虑降雨折减的降雨因子分量。

(2) 将3种降雨因子分量应用于某电站右岸库首边坡拉裂体变形监测资料分析中，对比结果表明改进后模型的精度较传统模型有所提高。该模型可避免降雨衰减系数K取0.8时对近一周降雨折减过大的问题，提高预测模型的准确性。

(3) 工程应用表明，优化后的回归统计模型能客观地反映拉裂体的变形规律，在拉裂变形体边坡的稳定安全预测方面具有一定的实际工程应用价值。但边坡变形监测数据受环境影响较大，部分测点测值规律性较差，考虑这些情况，应该在统计回归模型的构建以及降雨因子分量的优化上做进一步研究。

□