基于连续干旱游程的干旱特征分析与应用

覃丽华，张 鑫

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

干旱是最复杂的自然灾害现象之一，很大程度上直接或间接影响着经济、社会生产及自然生态环境的健康可持续发展；了解干旱事件的演变规律对旱情的防治、水资源的规划和管理具有重要意义。干旱历时、干旱烈度等特征对于旱情的防治、可用水资源的规划和管理非常重要[1]；同时，干旱历时和干旱烈度被认为是进行实时和长期干旱管理的两个基本特征，一直是研究人员关注的焦点[2]。

Copula联合函数被广泛应用于联合干旱变量而可以更好地分析干旱事件的演变规律[3]。采用Copula联合函数联合干旱变量前，需识别干旱并提取干旱变量数据。Herbst等[4]在1966年最先采用游程理论从月降水数据中识别干旱事件；李计等在2012年采用单阈值游程理论[5]提取干旱事件变量数据，此方法简单，但容易过度识别或识别不全干旱事件，容易降低识别干旱的精确度[6]；徐春晓等采用三阈值游程理论[7-9]提取干旱变量数据，但在游程阈值的选取上具有一定主观性与不确定性；王晓峰等[6]优化了干旱识别的截取水平，采用三截取水平识别干旱事件，提高游程理论识别实际干旱事件的可靠性。MONTASER等在2018年提出，与传统的不连续干旱游程方法(UDR，即游程理论)比较，连续干旱游程方法(CDR)在数据收集方面具有较高优势；采用不连续干旱游程来收集干旱特征变量，可能忽略在长期连续干旱中的短期极端干旱的实际潜力，且通常不同历时的UDR数据系列会因经常缺乏一系列干旱历时数据进而误差较大(比如，采用不连续干旱游程方法可能只能获得历时1和5个月的干旱，而无法获得历时2，3和4个月的干旱)，且当遇到分散和稀疏的极端数据时，用理论分布拟合观测数据时，尾部拟合会误差很大；然而，连续干旱游程在以上不足方面效果更好；采用连续干旱游程方法，可以确定更合适的Copula函数，优选的Copula函数在拟合和预测干旱的极端事件上效果更好，可以实际并准确地得到和预测干旱历时与干旱烈度的联合或条件概率并明显地降低拟合干旱历时和干旱烈度联合概率的不确定性[10]。

因此，本文基于陕西省榆林市5个气象站1960-2016年的逐月平均降水数据，采用连续干旱游程(CDR)数据收集方法[10]提取干旱历时和干旱烈度变量，进而分析榆林市干旱演变规律。气象站点详细信息见表1，榆林市及气象站点分布图见图1。

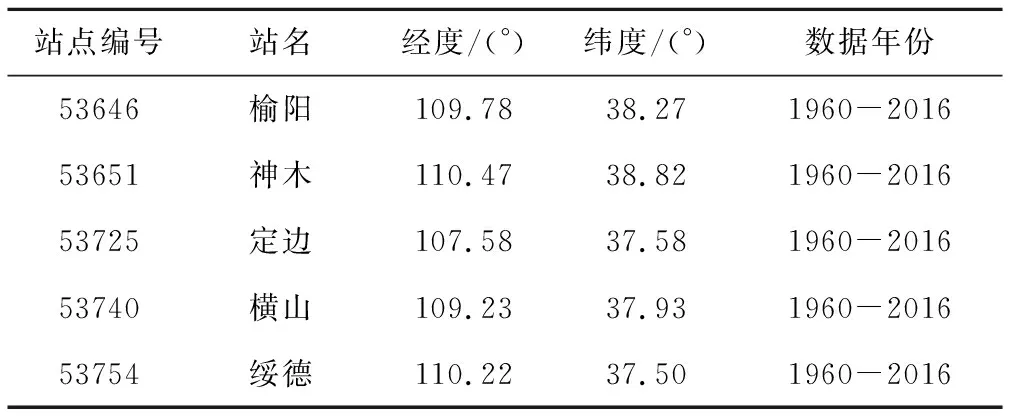
表1 榆林市气象站点信息Tab.1 Yulin meteorological stations information

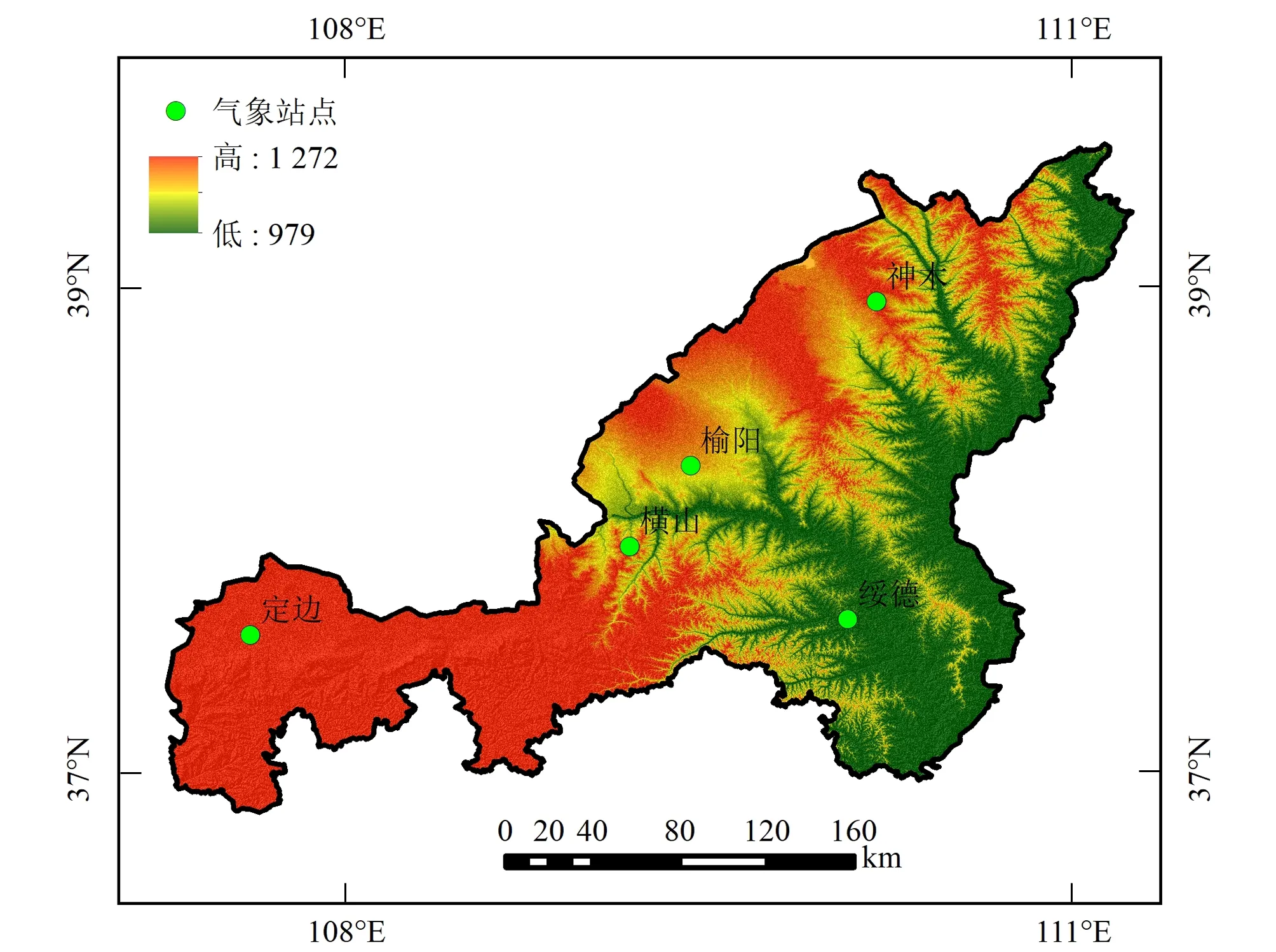
图1 研究区及气象站点分布图Fig.1 Study area and meteorological stations distribution

1 方 法

1.1 SPI

众观各描述干旱的指标，标准降水指数(SPI)通常具有数据计算简单和数据分析空间一致的两大优点，可以有效地实现多时间尺度的分析；且不同地点不同时间尺度下的降水频率是稳定的[11]。故本文选用基于降水数据的标准降水指数作为描述干旱的指标。3和6个月时间尺度的标准降水指数均被认为是农业干旱指数[12]。由于干旱具有累积效应且农作物具有一定的耐旱性，故短期的干旱可能对农作物而言影响并不太大，长期的干旱对农作物的影响就更为剧烈。故本文计算6个月时间尺度的标准降水指数作为描述干旱的指标。

1.2 连续干旱游程(CDR)

长历时不连续干旱游程(UDR)可以近似用若干短期连续干旱游程或不同历时的非独立干旱游程(CDR)来表示，用连续干旱游程(CDR)方法采用移动窗口技术一个历时6个月独立干旱(UDR)可以分出6个历时1月，5个历时2月，4个历时3月，3个历时4月，2个历时5月和1个历时6月的连续干旱游程[10]。

为提高识别干旱的准确度，本文采取王晓峰等[6]优化的三截取水平游程理论进行干旱事件的判别，提高识别干旱的可靠性，再在此游程理论基础上采用连续干旱游程提取干旱历时 和干旱烈度 变量数据。

1.3 Copula函数

在运用Copula函数联合干旱历时与干旱烈度变量之前，需要度量变量之间的相关性。本文通过采用Spearman、Pearson和Kendall秩相关性检验度量干旱历时和干旱烈度间的相关性。

Copula是一种联合分布函数，在[0,1]区间上服从均匀分布；设F为n维分布函数，各变量的边缘分布分别为F1，F2，…，Fn；则存在n维Copula函数C，对于任意x∈Rn，其分布函数满足下式[3,6]：

F(x1，x2，…，xn)=C[F(x1)，F(x2)，…，F(xn)]

(1)

式中：x1，x2，…，xn为观测样本；F(x)为边缘分布函数。

本文采用5种Copula函数：Clayton Copula、Frank Copula、Gumbel Copula、Gaussian Copula和t Copula拟合二维干旱变量联合分布。采用Matlab内置的函数(极大似然法)估计Copula函数的参数。

近代世界的国际关系是随着世界的全球化趋势而逐渐展开的。通常认为，世界第一次全球化是1750年前后开始并以欧洲国家特别是英国为主导。殖民主义是推动世界全球化的主要方式。中国在鸦片战争的背景下被迫融入这一世界大潮。就中国近代体育而言，也是在这一体育全球化过程中受到西方文化的直接影响而经历了一个从无到有的创建过程。从体育对外关系的角度来看，当时中国主要依次借助欧洲、日本和美国先进体育文化影响而逐渐建构起较为完整的中国近代体育体系。在此基础上，民国初年的中国体育界出现了对外交往的主动尝试，并将体育对外交往的触角首先伸向了东南亚地区，且取得了较好的外交成果，从而给我们留下了深刻的历史启示。

使用均方根误差(RMSE)来评价二维Copula函数的拟合优劣，RMSE值越小越优，其计算式如下：

(2)

式中：Pei为理论频率；Pi为经验频率。

1.4 二维变量概率分布

在分析干旱时，比较注重分析干旱联合累积概率及组合重现期。设干旱历时与干旱烈度的边缘分布函数分别为FD(d)与FS(s)，干旱历时与干旱烈度两变量的联合累积概率为分布函数：

F(d，s)=P(D≤d，S≤s)=C[FD(d)，FS(s)]

(3)

两变量的联合超越概率为：

P(D≥d，S≥s)=1-FD(d)-FS(s)+F(d，s)

(4)

两变量联合重现期T0与同现重现期Tα分别为：

(5)

(6)

2 结果与分析

2.1 干旱变量的特征

根据不连续干旱游程(UDR)和连续干旱游程(CDR)两种方法收集研究区站点的干旱历时和干旱烈度数据。

由图2榆阳站干旱历时和干旱烈度的散点图及边缘分布直方图所示，与UDR方法相比，CDR方法识别提取的数据系列含有较多的极端数据，有助于理论分布拟合实测较高极值部分，进而有助于减小最优理论分布与实测数据的尾部拟合误差。

图2 基于两种方法的榆阳站干旱历时和干旱烈度的散点图及边缘分布直方图Fig.2 Scatter plot of drought duration and severity, together with their marginal histograms based on two different data collection methods at Yuyang Station

此外，榆阳站的结果与其他站点情况相似。基于两种方法4个其他站的干旱历时和干旱烈度的散点图见图3。

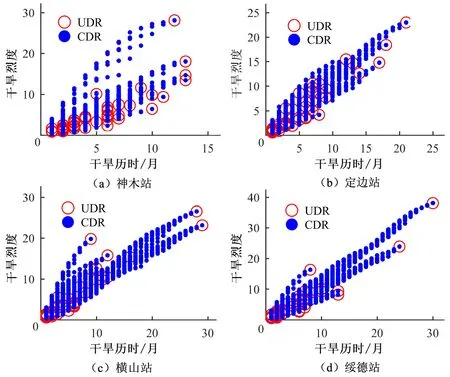
图3 基于两种方法的其他4个站的干旱历时和干旱烈度散点图Fig.3 Scatter plot of drought duration and severity based on UDR method and CDR method at four different stations

表2 干旱历时和干旱烈度相关性分析Tab.2 The correlation coefficient between drought duration and severity under CDR method.

2.2 干旱变量的边际分布

应用Copula函数建立双变量联合概率分布之前，需要鉴别和确定每个变量的最佳边际分布。为此，将正态分布、对数正态分布、伽马分布、指数分布、韦布尔分布和泊松分布六个分布函数拟合干旱历时和干旱烈度变量数据。

应用RMSE拟合优度检验优选干旱历时和干旱烈度的最佳边际分布。表3列出了干旱历时和干旱烈度的拟合优度检验结果以及最优拟合分布站次比。由表3知，在拟合干旱历时，指数分布的最优分布站次比为100%，即所有站点干旱历时的最佳拟合分布函数均为指数分布；在拟合干旱烈度时，神木站和绥德站的最优分布为对数正态分布，榆阳站和横山站的最优分布为指数分布，定边站的最优分布为韦布尔分布。从各站点干旱历时与干旱烈度最优分布的理论概率与经验概率对比图(图4)，可以看出边际分布函数的拟合效果较好。

2.3 优选Copula函数

本文对比了用Clayton，Frank，Gumbel，Gaussian和t Copula共5种常见Copula函数拟合研究区各个站点的干旱历时与干旱烈度两变量的联合概率分布。采用极大似然法估计Copula函数的参数。最后，优选具有最小RMSE值的Copula函数为拟合最佳的干旱历时与干旱烈度两变量联合概率分布函数。

研究区域所有站点的五种Copula函数拟合的两变量联合概率结果见表4。根据表4知，绥德站的最优分布函数为Frank Copula，榆阳站和横山站的最优分布函数为Gumbel Copula，神木站和定边站的最优分布函数为Gaussian Copula。

表3 基于CDR方法的变量拟合优选结果Tab.3 The results of goodness of fit tests of drought duration and severity data derived from CDR method

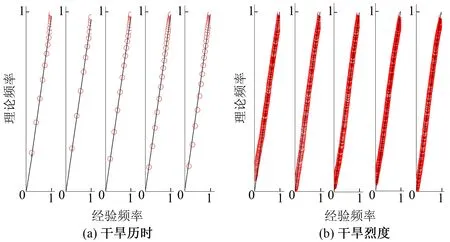
图4 干旱历时和干旱烈度最优分布理论概率与经验概率对比图Fig.4 Comparison of the theoretical and empirical probability of drought duration and severity

基于各个站点优选的Copula函数的理论概率与经验概率对比图(见图5)，知各个站点优选的Copula函数的拟合效果较好。

2.4 概率分布与重现期计算

应用各站点优选的Copula函数分析干旱历时与干旱烈度的联合概率分布及组合重现期。由式(3)求得5个站点干旱历时与干旱烈度的联合累积概率，分别如图6所示。

图5 各站点最优Copula函数理论概率与经验概率对比图Fig.5 Comparison of theoretical and empirical probability of drought duration and severity

分析5个站点的联合概率图知，5个站点的干旱联合累积概率均随干旱历时和干旱烈度的增大而增大。且均具有以下特征：当干旱历时不超过5个月或干旱烈度不超过5时，历时等值线和烈度等值线均较稀疏、等值线间梯度较大；随着干旱历时与干旱烈度均增大，联合累积概率迅速增大；随着干旱历时D不变但干旱烈度S不断增大时，联合累积概率只在烈度S为1～D+1值时才迅速增大，若D+1值大于5时，联合累积概率只在烈度S为1～5值时才迅速增大；随着干旱烈度S不变但干旱历时D不断增大时，联合累积概率只在历时D为1～S+1值时才迅速增大，若S+1值大于5时，联合累积概率只在历时D为1～5值时才迅速增大。当干旱历时超过5个月且干旱烈度超过5时，历时等值线和烈度等值线均较密集、等值线间梯度较小；随着干旱历时与干旱烈度不断增大，联合累积概率以越来越小的变率缓慢增大。总体来看，5个站点所在区域干旱以短历时短烈度、短历时高烈度及长历时低烈度情况居多。

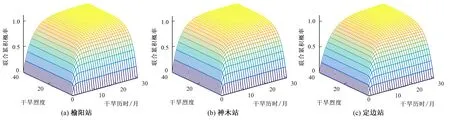
图6 干旱历时与干旱烈度联合累积概率Fig.6 Three-dimensional diagram of the joint probability of drought duration and severity

由式(5)、式(6)求得5个站点干旱历时与干旱烈度的组合重现期，分别如图7、图8所示。由图7可知，当干旱历时和干旱烈度为历史最大值时，榆阳站、神木站、定边站、横山站和绥德站干旱的联合重现期(且重现期)分别接近410、185、500、 435和320 a；由图8可知，当干旱历时和干旱烈度为历史最大值时，榆阳站、神木站、定边站、横山站和绥德站干旱的同现重现期(或重现期)分别接近127、52、153、78和33 a。总体来看，5个站点的同现重现期和联合重现期随着干旱历时和干旱烈度的增加呈先缓后陡的增加趋势。

图7 干旱历时和干旱烈度且重现期及其等值线Fig.7 The co-occurrence return period and its contour plot of drought duration and drought severity

表4 Copula函数的拟合优选结果Tab.4 The results of goodness of fit tests of the Copula function

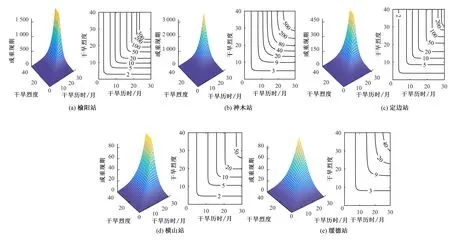
图8 干旱历时和干旱烈度或重现期及其等值线Fig.8 The joint return period and its contour plot of drought duration and drought severity

3 结 论

本文根据陕西省榆林市5个气象站1960-2016年的逐月标准化降水指数(SPI)序列，通过传统的游程理论(不连续干旱游程，UDR)与连续干旱游程(CDR)方法提取干旱历时和干旱烈度两个干旱特征变量，应用Copula函数联合干旱历时和干旱烈度，通过RMSE准则优选拟合最佳的Copula函数，通过Copula函数分析干旱历时和干旱烈度的联合概率与组合重现期。据此可为区域内旱情的防治、水资源的规划和管理工作提供理论依据。综合分析结果表明：

(1)与UDR方法相比，CDR方法识别提取的数据系列含有较多的极端数据，有助于理论分布拟合实测较高极值部分，进而有助于减小最优理论分布与实测数据的尾部拟合误差。

(2)基于CDR数据收集方法，经拟合优选知，干旱历时最适分布为指数分布；干旱烈度的最适分布则各站有不同，其中，神木站和绥德站的最优分布为对数正态分布，榆阳站和横山站的最优分布为指数分布，定边站的最优分布为韦布尔分布；同干旱烈度一样，干旱历时与干旱烈度的联合最适分布也依各站而不同，其中，绥德站的最优分布函数为Frank Copula，榆阳站和横山站的最优分布函数为Gumbel Copula，神木站和定边站的最优分布函数为Gaussian Copula。

(3)榆林市干旱联合累积概率随干旱历时与干旱烈度增大而增大；组合重现期随干旱历时与干旱烈度的增大而呈先缓后陡的增加趋势。

□