锦屏一级拱坝黏弹性工作性态反演分析

王少伟,徐 丛,苏怀智

(1.常州大学环境与安全工程学院，江苏，常州 213164；2.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏 南京 210029；3.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098)

高坝的运行安全是当前坝工领域非常关注的问题，其核心就在于评估大坝的现状结构性态[1]。变形作为混凝土坝运行性态的最直观反映，是评价大坝结构性态转异和长效服役健康状况的重要指标[2]。基于数值模拟的正分析是评价和诊断混凝土坝结构性态的重要方法之一。对此，国内外学者进行了大量研究，并取得了非常有价值的成果。Campos等[3]通过仿真分析，发现Mequinenza混凝土坝的异常趋势性变形主要是由湿胀所导致的坝体施工层面开裂而引起；Wu等[4-5]对锦屏一级拱坝施工期和初次蓄水期的工作性态进行了仿真和反演分析，表明坝体后期温升约5～6℃，坝体混凝土和坝基岩体的弹性模量约为设计值的1.65倍；Jin等[6]基于数值模拟和工程类比分析，提出了以坝踵开裂至帷幕轴线、坝体混凝土屈服体积突变和坝体位移突变作为拱坝安全性的评价因子，所得结论与Kölnbrein拱坝开裂现状相符；黄耀英等[7]基于黏弹性时变参数优化反演，定量解释了龙羊峡重力拱坝向上游侧的趋势性变形，认为主要因为坝体和基岩的黏滞系数较大，导致坝体自重引起的向上游侧时效变形需要较长时间才能收敛；王少伟等[8]提出了基于Drucker-Prager屈服函数的坝基岩体蠕变分段准则，实现了对高混凝土坝固有时效变形的量化分析。

基于原位变形监测数据建立多类数学模型，并据此定量解释拱坝的变形机理、识别大坝运行过程中的异常征兆，是目前评价大坝现状结构性态的另一重要途径。胡波等[9]基于变形监测数据的定性和定量分析，发现小湾拱坝蓄水初期坝体向上游侧的倾斜主要与水压作用下的库盘下沉有关；梁国贺等[10]通过统一坝体与坝基内外观监测系统的基准点，获得了溪洛渡高拱坝首次蓄水期的真实变形状态，发现河谷持续收缩已对该拱坝形成挤压效应。吴中如院士领衔的大坝安全监控团队先后建立了统计模型、混合模型、确定性模型以及融合人工智能算法的机器学习模型等，其中最为经典的是水压-周期性温度-时效(hydraulic-seasonal-time effect，HST)的3因子因果模型[11]。随着技术的进步和新工程问题的出现，上述模型也不断被优化和改进，Tatin等[12]考虑到HST模型中周期性函数表示的温度分量不能反映某一时段内气温明显低于或高于平均季节气温的情况，进而引入了日温差变形分量；Hu等[13]在HST模型中引入裂缝开度分量，定量解释了陈村拱坝下游面105 m高程水平裂缝对坝顶向上游侧异常趋势性变形的影响；Mata等[14]为研究气温日变化量对混凝土坝结构性态的影响，建立了坝体位移和气温两者日变化量之间的统计模型。

本文针对锦屏一级拱坝历年1 880 m高水位稳定期监测发现的坝体向下游侧位移持续增大的异常变形性态，根据现场监测数据和坝体混凝土徐变试验数据，总结坝体变形规律，在定性成因分析的基础上，反演坝体混凝土的黏弹性力学参数，以实现异常变形性态的定量分析。

1 基于监测数据的黏弹性滞后变形性态分析

锦屏一级拱坝位于四川省凉山彝族自治州境内的雅砻江干流上，是目前世界上已建的最高混凝土拱坝，最大坝高305 m，为混凝土双曲拱坝，由26个坝段组成。工程于2005年开工，2009年10月23日开始坝体首仓混凝土浇筑，2013年12月23日全面浇筑至坝顶高程，2014年8月24日首次蓄水至正常蓄水位1 880 m，之后坝体上游库水位在1 880 m与1 800 m之间呈年周期性循环。坝体垂线监测点下游面立视图如图1所示。

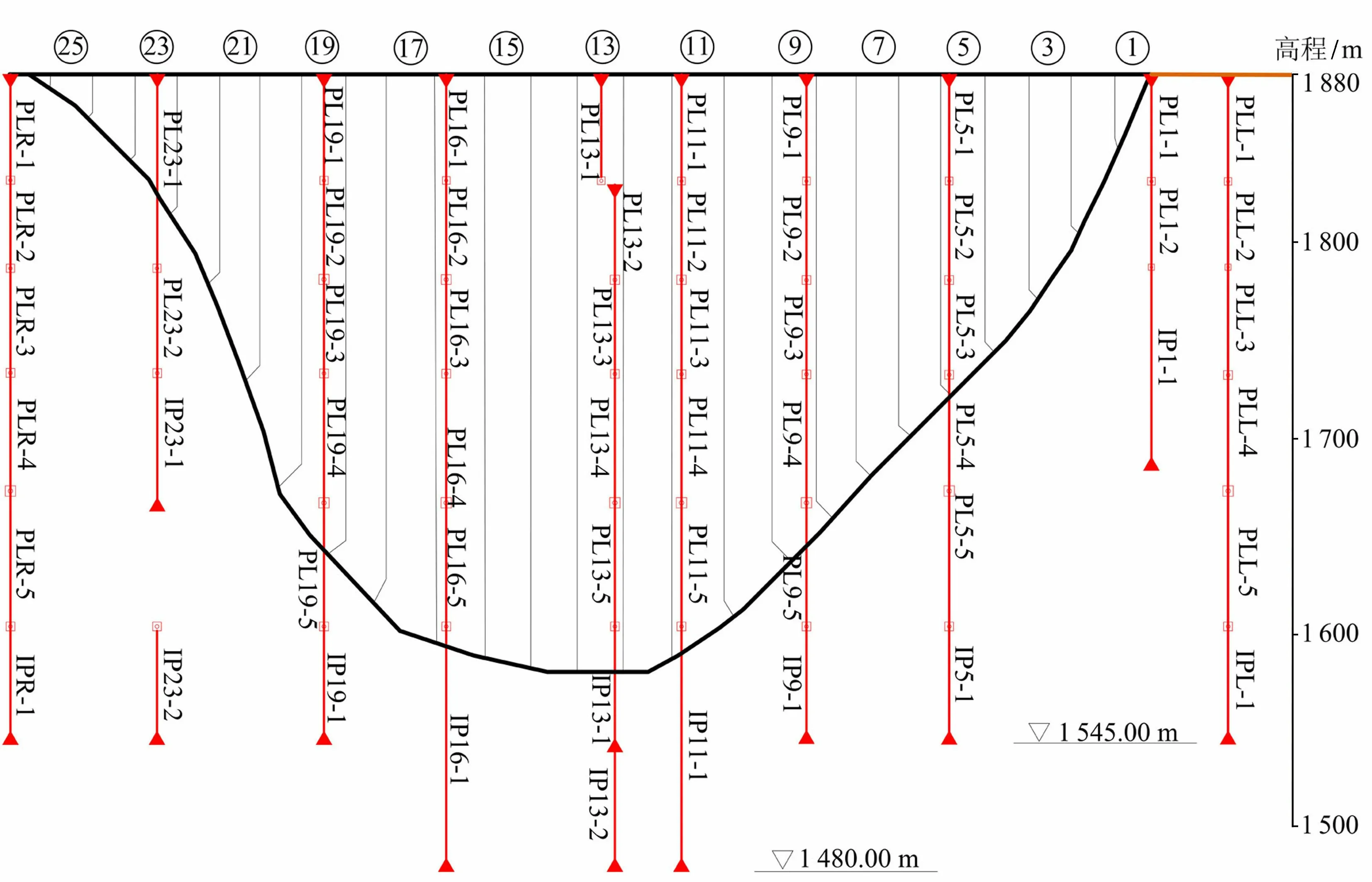
图1 坝体垂线监测点下游面立视图

坝体部分测点监测所得径向位移过程线如图2所示，其他测点的变形规律与此类似，其中位移向下游侧为正，向上游侧为负。从图2可以看出：坝体各部位径向位移与库水位之间具有较好的相关性；坝基变形较小，且主要是向下游侧发展的不可恢复变形。从2013年7月19日首次蓄水至1 800 m，至2014年6月再次下降至1 800 m水位，此阶段坝体中上部产生了明显的向上游侧趋势性变形，且该趋势性变形量值在后期基本保持不变，而温度监测资料表明坝体目前处于整体温升状态，且上述阶段内仍有小幅度增长，到2015年之后才基本趋于稳定，因此可认为后期水化热引起的坝体温升是上述向上游侧趋势性变形的成因之一；另外，从理论上讲，自重作用下坝体和坝基的黏性滞后变形对此也有较大贡献。蓄水至1 880 m或放水至1 800 m时，各年的位移监测值差异性较小，表明库水位在此兴利调节区间内变动时，所产生的变形变化量属于可恢复变形。

图2 坝体径向位移监测时间序列

2014年6月之后，库水位呈年周期性循环，且年内可主要划分为4个阶段，依次为：①上升期，每年6月中、下旬至7月中旬到9月中旬；②1 880 m高水位稳定期，持续时间长达97～167 d；③下降期，每年12月底至次年4月上旬到6月上旬；④1 800 m低水位稳定期，持续时间为半个月至2个月。从图2中可明显发现：1 880 m高水位稳定期，坝体各测点存在较明显的向下游侧持续增大的趋势性变形，而1 800 m低水位稳定期，坝体各测点的变形趋势是径向位移向上游侧持续增大，或者是已经产生的向下游侧径向位移持续减小。基于因果关系考虑，上述趋势性变形的成因可归结为2个方面：①坝体混凝土不可避免地存在着徐变变形，且实际工程试验中，主要为可恢复徐变[15-16]，使得坝体处于黏弹性工作状态，加、卸载后的变形发展具有明显的滞后效应；各年1 880 m稳定期变形发展速率较一致，且在长达167 d期间，未出现变形收敛的趋势，表明坝体黏滞系数较大，各稳定运行工况下黏弹性滞后变形需要较长时间才能趋于稳定。②环境温度变化效应，1 880 m高水位稳定期基本开始于每年的7月中旬至9月中旬，持续到12月底，而坝址处气温年最高值和最低值分别出现在每年的7月底和1月初，因此上述1 880 m水位稳定期属于坝址气温年周期性循环中的温降阶段，根据拱坝变形机理，温降将引起坝体向下游侧变形；而1 800 m低水位稳定期则属于温升阶段，气温变化引起的坝体温度变形是向上游侧的。由此表明，1 880 m高水位稳定期监测发现的短期趋势性变形，是由水压荷载作用下的黏弹性滞后变形效应和环境温降效应所共同引起的。

为进一步分析坝体混凝土徐变引起的黏弹性滞后变形，从图3所示水库蓄、放水过程中坝体PL11-1测点径向位移与库水位关系曲线可以看出：水位高于1 840 m时，上升阶段和下降阶段过程中径向位移与库水位之间的整体规律基本一致，且不同年份之间基本相同，即加、卸载情况下的变形发展路径是相互平行的，由此也表明坝体处于黏弹性工作状态；同一水位下，各年上升阶段的位移值基本相同，而下降阶段位移的位移值略有差异，其主要是由各年1 880 m高水位稳定期持续时间的长短不一致所引起的，持续时间越长，徐变变形量越大，而同年上升阶段和下降阶段之间的位移差值则是由上述稳定期内的黏弹性滞后变形和环境温降效应共同引起的向下游侧变形。库水位低于1 840 m时，库水位下降阶段由于黏弹性变形的滞后恢复，使得上升阶段和下降阶段2曲线之间的间距变小。2015年库水位下降过程中，在1 824～1 833 m水位之间出现了短期内的升降波动，初次和第2次下降至1 824 m时，径向位移相差3 mm，而此阶段时间间隔较短，其他环境因素的变化相对较小，表明在库水位下降引起的整体卸载过程中存在明显的滞后恢复变形。

图3 水库蓄、放水过程中PL11-1测点径向位移与库水位关系曲线

综上，基于坝体径向监测位移分析结果表明：锦屏一级拱坝目前处于黏弹性工作状态，且坝体黏滞系数较大，导致水压荷载作用下黏弹性滞后变形的发展和消除所需时间较长，与温度变形叠加后，共同引起了锦屏一级拱坝1 880 m高水位稳定期坝体向下游侧位移持续增大这一异常变形性态，因此需要对其成因进行定量分析解释。

2 坝体混凝土黏弹性力学参数试验分析

混凝土在定常持续应力作用下变形随时间不断增大的现象称为徐变，多采用徐变度来描述定常荷载作用下混凝土徐变与加荷龄期和持荷时间之间的关系。在大体积混凝土温控问题中，目前广泛采用的是朱伯芳院士提出的8参数徐变度公式[16]：

C(t,τ)=(x1+x2τ-x3){1-exp[-x4(t-τ)]}+

(x5+x6τ-x7){1-exp[-x8(t-τ)]}

(1)

式中：xi(i=1,2，…，8)为根据试验确定的参数；t和τ分别为持荷时间和加荷龄期。

大坝蓄水前，坝体混凝土已有较长龄期，可将式(1)中龄期对徐变度的影响部分视为定值，进而上述徐变度公式可转变为双指数函数形式。在混凝土坝长期变形的计算模型方面，基于时间微分形式的元件组合模型目前使用较多，通过Hook体、Kelvin体、村山体、Newton体和Bingham体等元件的组合，来表征混凝土和岩体的变形特征，并据此进行数值模拟分析[8]。以2个Kelvin体串联而成的广义Kelvin模型如图4所示，常应力下的时效变形为

(2)

式中：EK1和EK2为延迟弹性模量；ηK1和ηK2为黏滞系数；σ为应力。

因此，可采用图4所示广义Kelvin模型表征坝体混凝土徐变引起的黏弹性工作性态，并参照岩土工程中基于蠕变试验的岩体蠕变模型辨识及参数反演方法[17]，对坝体混凝土徐变度曲线采用ε(t)=b1[1-exp(-b2t)]+b3[1-exp(-b4t)](其中b1、b2、b3、b4为拟合参数)进行拟合，再根据拟合系数来确定黏弹性本构模型中的力学参数[18]：EK1=1/b1，EK2=1/b3，ηK1=1/(b1b2)，ηK2=1/(b3b4)。

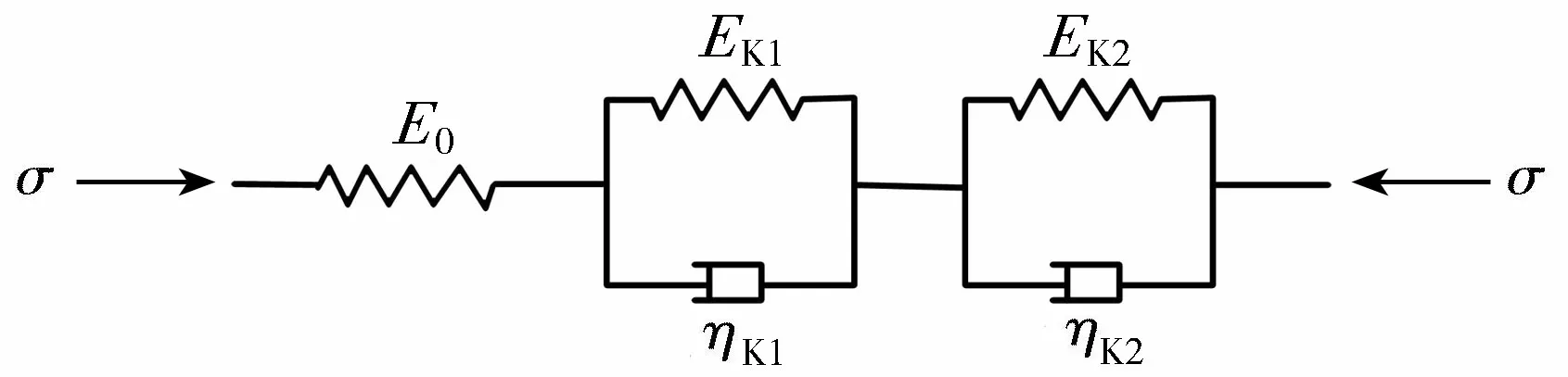
图4 双Kelvin体表征的坝体混凝土黏弹性本构模型

锦屏一级拱坝坝体C35全级配混凝土的徐变度曲线试验值和广义Kelvin模型的拟合值如图5所示。坝体混凝土瞬时弹性模量试验值如表1所示，按照式(1)拟合混凝土徐变度曲线后计算得到广义Kelvin模型中的延迟弹性模量和黏滞系数如表2所示。随着龄期的增长和强度标号的提高，混凝土的瞬时弹性模量、延迟弹性模量和黏滞系数均明显增大。

表1 坝体混凝土不同加载龄期瞬时弹性模量E0试验值 GPa

表2 坝体混凝土延迟弹性模量和黏滞系数

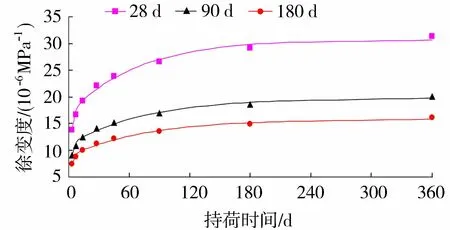
图5 C35混凝土不同加载龄期徐变度拟合曲线[19]

上述各力学参数之间的规律如图6所示。从中可以看出：混凝土瞬时弹性模量、延迟弹性模量和黏滞系数之间具有较好的正线性关系，且这种线性比例关系对3个标号的混凝土是基本相同的，因而可将这种正线性关系视为混凝土力学参数之间的一种固有规律。对于两力学参数之间的交点不为0，如瞬时弹性模量E0和延迟弹性模量EK1，可将其解释为只有当硬化到一定程度之后，混凝土才具备黏弹性；另一方面，本文徐变度试验的最早龄期是28 d，在此之前混凝土尚未硬化充分，其力学参数在实际工程应用中意义不大。

图6 双Kelvin体力学参数间关系

综上，鉴于反演分析过程中待反演参数较多时可能出现解答不唯一的实际情况，可利用上述混凝土力学参数之间的关系，来减少待反演参数的数量。

3 坝体混凝土黏弹性力学参数反演分析

拱坝呈整体受力状态，且3个标号混凝土的瞬时弹性模量较接近，因此本文结合图6所示力学参数之间的正线性关系，在反演分析时仅以坝体混凝土的瞬时综合弹性模量为目标值，而延迟弹性模量和黏滞系数则根据图6所示规律进行计算。

3.1 有限元模型

锦屏一级拱坝整体有限元分析模型如图7所示，其中坝基范围为：以拱冠梁坝踵和坝趾、左右岸坝肩最突出处、河床建基面分别为参考，向上下游、左右岸和河床深部分别延伸2倍坝高，坝顶以上延伸1.5倍坝高。模型以8结点6面体单元为主，局部采用6结点5面体单元，整体节点数和单元数分别为953 143和920 165，坝体的节点数和单元数分别为36 079和29 840。边界条件定义为：上游水位采用计算日当天实测值，由于水垫塘的存在，下游水位长期保持在1 645 m；坝基底部为三向固定约束，4个侧边界为法向固定约束。

图7 有限元计算模型

有限元数值模拟过程起始于2009年10月23日的坝体首仓混凝土浇筑，持续到2018年12月31日。结合实际蓄水和坝顶垂线初始监测情况，首先分级施加坝体自重和1 716 m水位以前的上游库水压力，并将其作为初始应力场，其中坝体自重分61个荷载步模拟，每荷载步内坝体混凝土上升高程为5 m，持续20 d。在此基础上，2012年11月30日之后，模拟库水位的周期性循环过程，有限元计算增量步时间间隔为1 d，上游水压力与当日实测库水位对应。

3.2 反演方法及材料参数组合

考虑到本工程地质条件的复杂性，且监测表明该拱坝变形主要是由坝体混凝土所引起，因此数值模拟时仅考虑坝体混凝土的黏性变形，而忽略坝基的黏性变形，并通过坝体的相对变形来进行监测异常变形性态的解释。采用HST混合模型进行反演，具体分两种情况：弹性反演法和黏弹性反演法，两者分别在坝体混凝土弹性和黏弹性的假设下，通过有限元计算水压分量，再结合位移监测资料，按式(3)所示HST混合模型拟合得到有限元水压分量的调整系数，进而按式(4)反演坝体混凝土瞬时弹性模量值。

(3)

(4)

根据2011年12月1日至2014年8月24日期间的位移监测资料，锦屏一级拱坝的业主单位反演得到坝基中Ⅱ类、Ⅲ1类和Ⅲ2类岩体以及C40、C35和C30混凝土的弹性模量分别为43.2 GPa、18.4 GPa、10.8 GPa、38.2 GPa、37.4 GPa和36.6 GPa。本文分析时，坝基岩体采用此反演值。上述反演采用的是弹性反演法，所得坝体混凝土弹性模量是瞬时弹性变形和黏弹性滞后变形的综合反映，因而该反演值小于同标号混凝土的瞬时弹性模量。对此，反演时拟定两种反演初值，将有限元计算时坝体混凝土的瞬时弹性模量分别取为38 GPa和48 GPa，并据此按图6所示力学参数间关系式计算广义Kelvin模型中的其余4个黏弹性参数。各计算组合下的力学参数如表3所示。

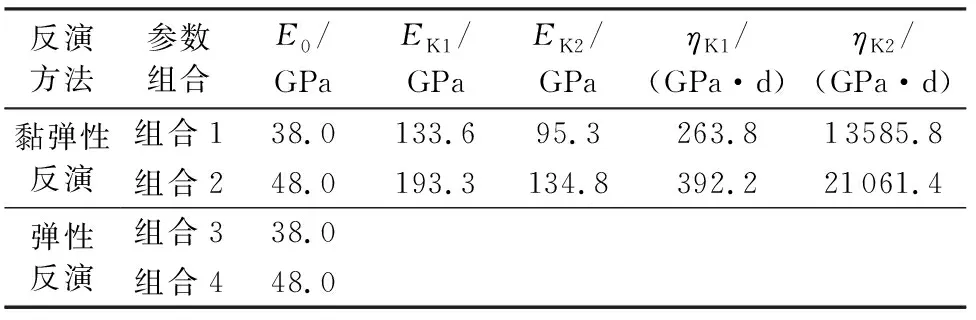
表3 坝体混凝土待反演力学参数初值

3.3 反演结果分析

组合2和组合4两种材料参数情况下，坝顶PL11-1测点的径向位移过程线如图8所示，其中黏弹性滞后位移为相同计算水位下黏弹性总位移与弹性位移之差。从中可以看出：在相同瞬时弹性模量情况下，考虑混凝土徐变所引起的黏弹性滞后变形后，总位移明显增大。以PL11-1测点为例，首次达到1 880 m水位时，弹性位移和黏弹性滞后位移分别为24.18 mm和7.63 mm，后者所占比例为31.6%；而常用的混合模型反演法中，是在弹性有限元计算水压分量的基础上乘以调整系数，并将其作为实测位移中的水压分量值，因此不考虑上述黏弹性滞后位移的情况下，将导致该调整系数偏大，进而使得反演得到的瞬时弹性模量偏小(此时反演得到的弹性模量实际为瞬时弹模和延迟弹模按弹簧串联理论得到的等效转换值)；另一方面，在历年1 880 m高水位稳定期，黏弹性有限元计算位移在此阶段呈明显增大的趋势，与位移监测规律基本一致，由此表明水压荷载作用下坝体混凝土徐变所引起的黏弹性滞后变形是锦屏一级拱坝1 880 m水位稳定期监测所得坝体位移向下游侧持续增大的成因之一，因此需要在黏弹性力学参数反演分析的基础上，对该异常变形性态的成因进行定量分析。

图8 弹性和黏弹性有限元计算所得PL11-1测点径向位移

根据坝顶PL11-1测点2013年10月1日至2018年12月31日期间的径向位移监测数据，所建HST混合模型的系数如表4所示，据此反演得到的坝体混凝土力学参数如表5所示。相同反演方法不同初值假设情况下，反演误差均在2%左右，满足工程分析精度要求，表明混合模型反演法具有较好的初值适应能力。弹性反演时，反演所得混凝土弹性模量为35.5 GPa，与前期业主反演值和试验值较为接近。对于弹性反演和黏弹性反演之间的关系，根据图3所示广义Kelvin模型和弹簧串联理论，采用等效弹性模量来综合反映瞬时弹性变形和黏弹性滞后变形时，以组合2为例，其值应介于47.3 GPa和29.4 GPa(1/(1/47.3+1/189.4+1/132.3)=29.4)之间；文中第1个Kelvin体的黏滞系数较小，加载后变形发展较快，而第2个Kelvin体的黏滞系数非常大，主要用来描述混凝土持荷较长时间之后的徐变继续增长，因而等效弹性模量应更接近于Hook体与第1个Kelvin之间的等效值37.8 GPa(1/(1/47.3+1/189.4)=37.8)，而弹性反演得到的此等效值为35.5 GPa，两者较接近。由此表明，基于弹性有限元水压分量，通过混合模型反演得到的弹性模量实际是混凝土瞬时弹性模量与延迟弹性模量的等效值。

表4 混合模型拟合回归系数

表5 坝体混凝土力学参数反演值

根据弹性和黏弹性有限元水压分量所建HST混合模型的各分量分离值如图9所示。两种情况下，各分量的演变规律和量值基本一致，差异性就在于后者考虑了水压荷载作用下的黏弹性滞后变形，使得所分离的水压分量在1 880 m水位稳定期有明显的持续增长趋势；组合2和组合3所建模型的温度分量年极小值分别为-1.67 mm和-1.94 mm，年极大值分别为6.45 mm和7.82 mm，且极值出现的时刻完全一致，由此表明基于弹性水压分量所建混合模型分离得到的温度分量年变幅偏大，其原因在于该模型对于1 880 m水位稳定期坝体向下游侧位移持续增大的现象是完全基于温度分量来解释的，进而将黏弹性滞后水压变形增量也归入到温度分量中。以2018年1 880 m水位稳定期为例，此阶段PL11-1测点实测径向位移增量为10.16 mm，而分量分离值中，水压分量和温度分量的增量分别为3.17 mm和7.73 mm，因而可从定量的角度认为上述变形增量中黏弹性滞后变形效应和环境温降效应各自的贡献度分别为29.1%和70.9%。

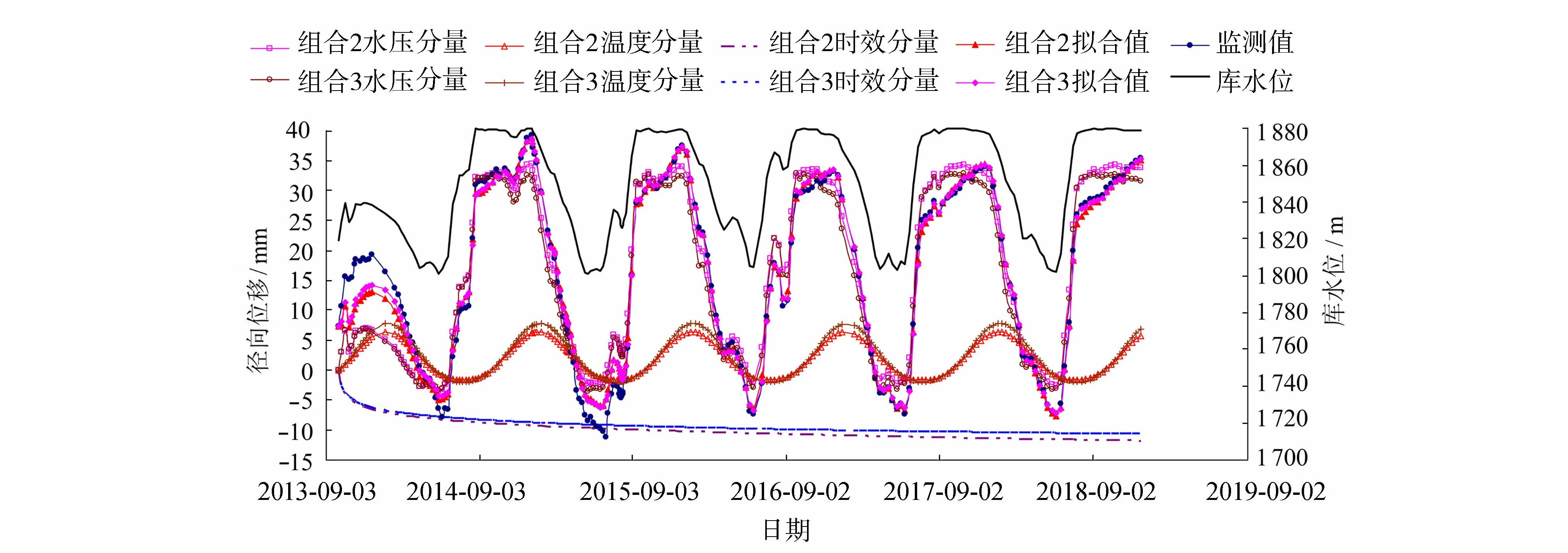
图9 PL11-1测点径向位移HST混合模型各分量分离值

对于锦屏一级拱坝，每年1 880 m高水位稳定期持续时间较长，上述黏弹性滞后变形效应在此阶段的影响较显著，因此建议今后对该拱坝建立变形监控模型时，应在HST模型的基础上引入黏弹性滞后水压分量，以便精确诊断和评价大坝的真实工作性态。

4 结 语

针对锦屏一级拱坝历年1 880 m高水位稳定期坝体向下游侧位移持续增大的异常现象，利用监测位移对该拱坝的变形性态进行了反演分析，表明该拱坝目前处于黏弹性工作状态，监测发现的异常变形性态是由水压荷载作用下黏弹性滞后变形效应和年周期环境温降效应所共同引起。采用广义Kelvin模型表征坝体混凝土的黏弹性本构模型时，徐变试验数据拟合结果表明该模型中的5个参数之间具有较好的正线性关系。利用2013—2018年的坝顶径向位移反演得到的该拱坝坝体混凝土弹性模量的等效值、瞬时值和2延迟值分别为35.5 GPa、47.3 GPa、189.4 GPa和132.3 GPa，2黏滞系数分别为383.8 GPa·d和20 574.6 GPa·d。建议今后在对该拱坝建立变形监控模型时，应引入黏弹性滞后水压分量，并对该分量构建合理的数学模型因子。