分位数回归和GAMLSS模型在非一致性洪水频率分析中的比较
2020-10-18屈春来刘章君鲁东阳
李 婧, 闫 磊, 屈春来, 刘章君, 鲁东阳
(1.河北工程大学水利水电学院,河北 邯郸 056000; 2.江西省水利科学研究院,江西 南昌 330029)
洪水频率分析对水利工程建设至关重要,一致性假设一直是洪水频率分析的基本假设条件,但受到气候变化以及人类活动的影响,降雨时空分配过程以及流域下垫面的产汇流条件发生了改变,导致洪水频率分析的一致性假设受到挑战[1-4],传统频率计算方法构建模型的合理性受到质疑。因此,在变化环境下进行洪水序列的非一致性频率分析具有重要意义。非一致性频率分析成为变化环境下洪水分析计算的研究热点之一[2,5]。当前最常用的非一致性频率分析方法是采用基于位置、尺度和形状参数的广义可加模型(generalized additive models for location scale and shape, GAMLSS)构建非一致性概率分布模型。Villarini等[6-7]应用GAMLSS模型分别对罗马降水序列以及美国Little Sugar Creek流域的年最大洪峰序列进行了趋势分析,取得了较好的拟合效果。江聪等[8]认为运用传统方法对水文序列均值的趋势性进行分析相对片面,通过GAMLSS模型引入方差和偏态系数等参数对宜昌站多年年流量序列进行了趋势分析。张冬冬等[9]采用GAMLSS模型研究了大渡河流域年最大日降水极值序列的非一致性,发现GAMLSS模型可以模拟水文序列的方差、偏态系数等统计参数的非线性变化趋势。
然而,GAMLSS模型构建过程较复杂,首先需要选定概率分布模型,然后假定所选概率分布模型统计参数与协变量的关系,模型统计参数多且结构较复杂。为解决这一问题,董洁等[10-12]尝试引入非参数方法进行非一致性水文频率分析。Koenker等[13]首先提出了分位数回归方法研究样本点在不同的分位数下随时间变化情况,随着该方法的进一步研究开发,目前广泛应用于水文分析中。Mazvimavi[11]利用分位数回归方法对津巴布韦的降雨序列变化进行分析。Barbosa[12]等运用分位数回归对波罗的海海平面变化进行分析,发现极大值处的斜率趋势性更大。Wang等[14]利用分位数回归方法对美国南部月降雨变化情况进行分析。冯平等[15]利用分位数回归方法分析滦河流域年降雨、径流序列的变化特性,发现流域年降雨序列总体保持一致性,而年径流序列受人类活动等影响表现为减小趋势,且高分位数的减小速率大于低分位数。本文选取位于我国不同气候区的渭河流域和珠江流域的5个代表站点的年最大洪水序列作为研究对象,综合定性分析和定量分析,对比分位数回归模型与GAMLSS模型在进行非一致性洪水频率分析时的表现。
1 流域概况和数据资料
渭河流域发源于甘肃省渭源县鸟鼠山,流经甘肃、陕西两省,至渭南市潼关县汇入黄河,河长818 km,流域面积134 766 km2,位于北纬33°40′~37°26′,东径103°57′~110°27′之间[16-17]。渭河中下游径流的年际变化表现为南部小、北部大。渭河干流秋季径流量最大,约占年径流量的38%~40%,夏季占32.8%~34.2%,春季占17.7%~19.1%,冬季为8.3%~9.9%。渭河中下游降雨集中于7—9月,而且多大暴雨,洪涝灾害较多。
珠江发源于云南省曲靖市马雄山,流经云南、贵州、广西、广东、湖南、江西6省及越南北部,在下游从8个入海口注入南海,全长2 320 km,流域面积45 369 km2。珠江流域由西江、北江、东江和珠江三角洲诸河等4个水系组成[18-19],流域多年平均降水量1 200~2 200 mm,年径流量超3 300亿m3,汛期4—9月径流量约占年径流量的80%,夏季(6—8月)则占年径流量的50%以上。
数据资料选取渭河的咸阳站、华县站、张家山站以及珠江流域的高道站和大湟江口站共5个重要站点的多年年最大洪水序列。5个站点的基本概况详见表1及图1。

图1 流域水文站点示意图
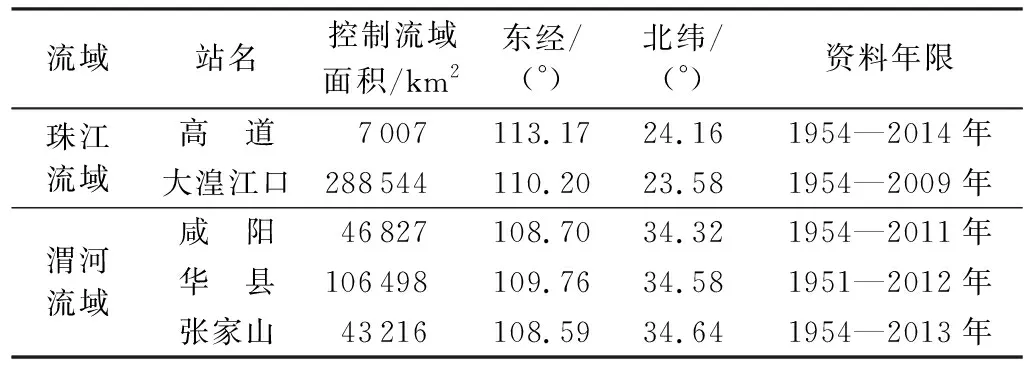
表1 各站点基本概况
2 研究方法
2.1 Mann-Kendall趋势检验方法
采用Mann-Kendall非参数趋势检验法检测降水和径流序列的长期变化趋势[20]。Mann-Kendall的检验方法[15,21]如下:
设Yi(i=1,2,…,n)为假设检验的随机变量,n为样本的观测长度,标准化检验统计量Zc为
(1)
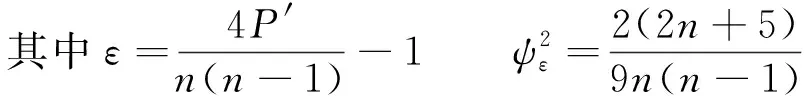
式中:P′为序列中所有对偶观测值(Yi,Yj,i
2.2 分位数回归法
分位数回归是依据因变量Y的条件分位数对自变量X进行回归,得到所有分位数下的回归模型;分位数回归对于模型中的随机干扰项不需要做概率分布假定,且估计量基本不受异常值的影响而更加稳定,可拟合出一簇曲线[15]。
假设随机变量Y的分布函数为F(y)=P(Y≤y),则Y的第τ分位数为
Q(τ)=inf{y:F(y)≥τ} (0<τ<1)
(2)
根据不同的分位数τ,可得到不同的分位数函数QY(τ)=ωiβ(τ)(QY(τ)为第τ分位数时Y的分位数函数,β(τ)为参数值,i=1,2,…,n)。分位数回归的目标函数是一个加权的绝对残差和,目的是使样本值与拟合值之间的距离最短。给定观测数据(ω1,y1),(ω2,y2),…,(ωn,yn),由此求解τ分位数的回归估计:
(3)
其中ρτ(·)是一个非对称的损失函数,定义为
可通过下式得到参数估计值,根据一个τ值确定一组β(τ)值:
(5)
2.3 GAMLSS模型
GAMLSS模型是基于位置、尺度、形状的广义可加模型,可以描述统计参数与协变量之间的线性和非线性关系,模拟随机变量分布函数类型广泛,适用于高偏度、高峰度、超峰度、平顶峰度等的随机变量序列[8,22]。
2.3.1模型的定义
在GAMLSS模型中,假设某一时刻t(t=1,2,…,n)的相对独立随机变量观测值yt的分布函数可以表示为F(yt|θt),其中θt=(θt1,θt2,…,θtf)为时刻t对应的分布统计参数向量,f为分布参数的个数,n为观测值的个数[8]。记gk(θk)为θk与相应的协变量Yk的单调函数关系,一般表示为
(6)
式中:ηk为长度n的向量;βk=(β1k,β2k,…,βIkk)T,为长度为Ik的回归参数向量;Yk为n×Ik的协变量矩阵;Zjk为已知的n×qjk矩阵;γjk为qjk维的正态分布随机变量向量;Zjkγjk为第j项随机效应[8]。
若不考虑随机效应的影响,则gk(θk) =ηk=Ykβk,针对位置参数μ、尺度参数σ和形状参数υ,以时间t为协变量的不考虑随机效应的全参数模型为
(7)
式中:μt、σt、υt分别为时变的位置参数、尺度参数、形状参数,可体现非平稳序列统计参数随时间的变化特征,因为形状参数对模型影响较大,所以一般不做考虑,可通过RS法[23]对β进行参数估计。
2.3.2模型的评价准则
选取GAIC准则(generalized akaike information criterion,简称GAIC)作为GAMLSS模型拟合评价指标,其值VGAIC的计算公式为
VGAIC=VGD+#df
(8)
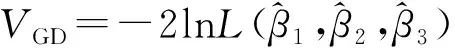
2.4 拟合优度检验
2.4.1正态QQ图
通过正态QQ图来分析最优模型的残差分布状况。正态QQ图是在平面坐标系中以经验残差为纵坐标、理论残差为横坐标绘制而成的,数据点与1∶1的线偏差越小,说明模型的拟合优度越好。
2.4.2模型概率覆盖率检验
通过模型概率覆盖率偏差数值的大小定性分析分位数回归模型与GAMLSS模型的拟合优度。模型概率覆盖率是各条分位数曲线覆盖范围内的实测样本点数量与总样本点数量的比值。计算模型概率覆盖率与对应分位数的差值,差值越小说明模型拟合优度越好。以50%分位数曲线为例,理论上讲,如果50%分位数曲线覆盖范围内的实测样本点数量与总样本点数量的比值越接近50%,则模型概率覆盖率与50%差值越小,模型拟和优度越好。
2.4.3Filliben检验
可通过Filliben相关系数来确定洪水序列最优分布形式,通过Filliben相关系数的大小来判定序列最优拟合分布,Filliben值越大则分布拟合优度越好[24]。
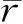
(9)
3 结果和讨论
3.1 Mann-Kendall趋势分析
使用R语言中trend程序包对各站点历史资料进行Mann-Kendall检验,显著性水平设定为5%,得出华县站、高道站、大湟江口站、咸阳站、张家山站5个站点P、Zc和S值见表2。

表2 各站点趋势性分析结果
华县站、高道站、咸阳站、张家山站4个站点通过显著性水平5%的检定,而大湟江口站通过显著性水平为10%的检定,同时根据Zc值正负关系可得出高道和大湟江口2个站点呈上升趋势,其他3个站点则呈下降趋势。故华县站、咸阳站、张家山站3个站点显著下降,高道站显著上升,而大湟江口站呈现不显著上升趋势。
3.2 GAMLSS最优模型拟合效果分析
3.2.1GAMLSS最优模型判定
本算例为选定最优概率分布类型,选取我国不同气候区的渭河、珠江流域的5个站点最大洪水序列为研究对象,时间t为协变量,AIC为评价准则,分别对比了P-Ⅲ分布、Gamma分布(简称GA分布)、Lognormal分布(简称LN分布)和GEV分布4种分布形式,通过正态QQ图判别拟合优度。每个站点每种分布类型根据位置参数和尺度参数分别随时间变化可形成4种不同的模型,总计16种,相应AIC取值详见表3。在表3模型代码中,以“L”表示位置参数,“S”表示尺度参数,“0”表示参数不变,“t”表示参数随时间协变量变化,此外粗体AIC值表示该站点的最佳模型。

表3 各站点模型AIC值对比
由此可得出华县站、高道站、咸阳站的最优模型为位置参数和尺度参数均随时间变化的Gamma分布,AIC值分别为1 051.84、1 057.64、955.81;大湟江口站最优模型则为位置参数随时间变化而尺度参数保持不变的Gamma分布,AIC值为1 155.26;张家山站最优模型则为位置参数随时间变化而尺度参数保持不变的Lognormal分布,AIC值为894.26。
图2给出了最优模型的正态QQ图的拟合优度检验结果。结果显示,根据AIC值选择的最优模型点均匀分布在1∶1直线附近,经验残差和理论残差基本一致,表明模型具有良好的拟合效果。
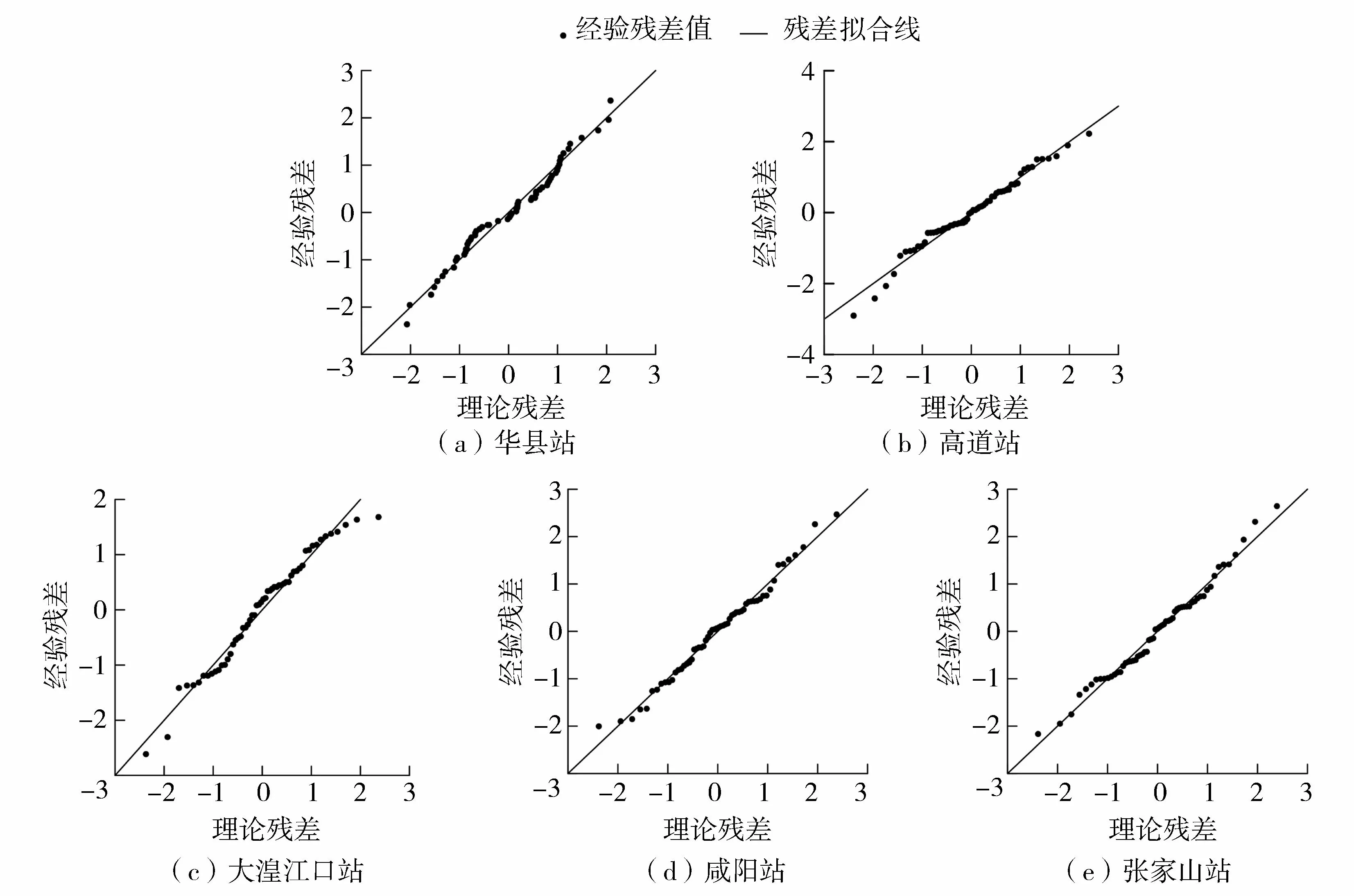
图2 各站点QQ图
3.2.2GAMLSS最优模型的定性分析
对于该算例的实际样本点来说,通过对比各站点GAMLSS模型的分位数曲线图,定性分析模型概率覆盖率,可得出华县站GAMLSS模型的概率覆盖率偏差最小为0.16%,最大为7.26%,高道站、大湟江口站、咸阳站、张家山站GAMLSS模型的偏差范围分别为1.56%~6.97%、1.43%~5.36%、0.17%~5.17%和0.08%~2.97%,具体见图3与表4。

图3 各站点基于GAMLSS模型的分位数曲线

表4 各站点不同分位数GAMLSS模型拟合优度对比
3.2.3GAMLSS最优模型的定量分析
通过对比Filliben相关系数进行定量对比分析,基于式(9)进行相应计算可得GAMLSS模型的Filliben相关系数:华县站为0.989 96;高道站为0.987 843;大湟江口站为0.986 808;咸阳站为0.994 089;张家山站为0.991 817。
3.3 分位数回归模型拟合效果分析
3.3.1分位数回归模型的定性分析
通过对比各站点分位数回归模型的分位数曲线图,可定性分析模型概率覆盖率,可得出华县站分位数回归模型下模型概率覆盖率偏差最小为0.81%,最大为4.84%;高道站、大湟江口站、咸阳站、张家山站分位数回归模型下偏差范围分别为0.08%~5.74%、0~0.36%、、0~2.59%和0.08%~1.61%,具体见图4与表5。

表5 各站点不同分位数回归模型拟合优度对比
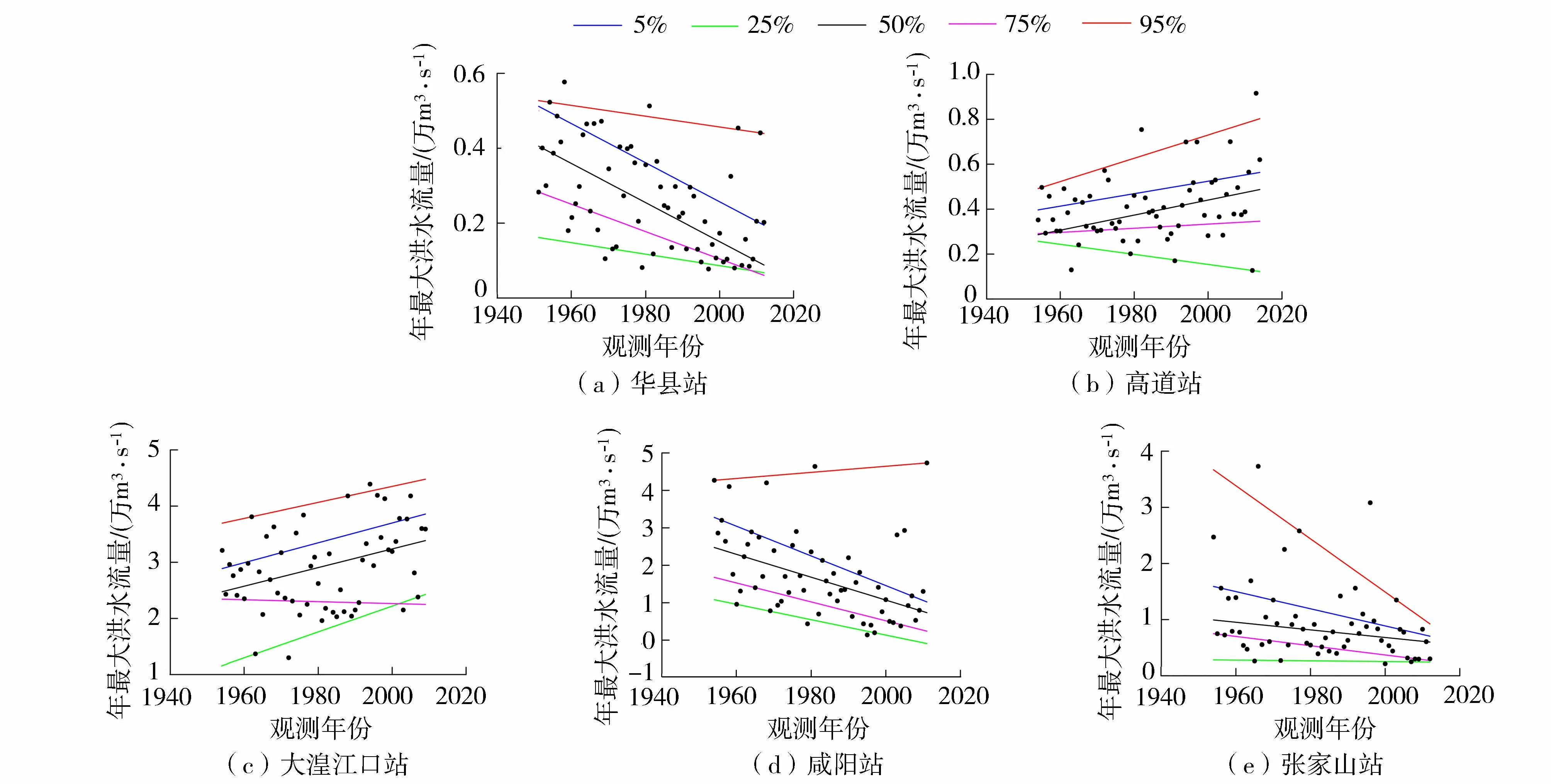
图4 各水文站基于分位数回归模型的分位数线
3.3.2分位数回归模型的定量分析
可通过对比Filliben相关系数进行定量对比分析,基于式(9)进行相应计算可得分位数回归模型的Filliben相关系数:华县站,0.983 076;高道站,0.983 149;大湟江口站,0.983 534;咸阳站,0.983 022;张家山站,0.984 437。
3.4 分位数回归模型与GAMLSS模型拟合效果比较
根据模型概率覆盖率进行定性分析,可发现各站点分位数回归模型均优于GAMLSS模型,华县站显示优度为0.3%~6.4%,高道站为1.6%~3.3%,大湟江口站为1.1%~5.4%,咸阳站为1.4%~5.2%,张家山站为0~1.8%;根据Filliben相关系数进行定量分析,两种模型Filliben相关系数较高,均通过显著性水平5%时,Filliben相关系数临界值为0.975的检验[25-28],两种模型的拟合效果GAMLSS模型优于分位数回归模型的范围基本位于0.3%~0.9%之间。基于Filliben相关系数的定量分析结果显示,GAMLSS模型拟合效果更好但优势不明显;基于模型概率覆盖率的定性分析结果表明,分位数回归模型的拟合效果更好。因此,综合上述定性分析和定量分析结果,总体来说,分位数回归模型的拟合效果更优。
4 结 论
a. 通过Mann-Kendall趋势检验可以得出5%显著性水平下华县站、咸阳站、张家山站3个站点显著下降,高道站显著上升,而大湟江口站呈不显著上升趋势。
b. 各站点在GAMLSS模型中拟合效果最好的分布,以Gamma分布为主、Lognormal分布为辅。华县站、高道站、咸阳站表现为Gamma分布下的位置参数和尺度参数均随时间变化的模型效果最佳,大湟江口站则为位置参数随时间变化而尺度参数保持不变的Gamma分布效果最佳,张家山站表现为Lognormal分布下的位置参数随时间变化而尺度参数保持不变的模型最佳。
c. 通过定性分析对比各站点两种模型概率覆盖率,发现分位数回归模型整体拟合效果优于GAMLSS模型。定量分析Filliben相关系数,分位数回归模型与GAMLSS模型拟合效果基本一致。故综合定性分析和定量分析可得出分位数回归模型的拟合效果优于GAMLSS模型。
d. GAMLSS模型可以考虑多种因素的影响以及更多的分布类型,进行更加复杂的模拟运算,但是统计参数较多,且统计参数与协变量的关系可能不只是线性,实际变化情况更加复杂,使得模型构建过程较为烦琐,而基于非参数方法的分位数回归模型构建更加简单且易于操作,模型拟合更加灵活,无须确定各项参数以及参数与协变量之间的复杂关系。
