印刷体数学字符根号的识别算法
2020-10-18吴家明李家豪包庆鹏
吴家明, 李家豪, 包庆鹏, 方 涛
(上海工程技术大学 数理与统计学院, 上海 201620)
数学公式在众多领域的文献资料中都大量存在.在数学、物理类科技期刊论文中,数学公式甚至占到整个论文篇幅的50%.它们在文档中有的独立占用一行,有的和其他文字混杂在一起.随着互联网的兴起,知识共享理念深入人心,但在对科技文献数字化时,由于数学公式本身的复杂性,目前的软件和硬件均不能完全正确识别文献中的数学公式.这些公式多以图像形式存储在各种格式的文件中,由于不能依据图像形式的公式对文章进行检索,读者就无法依据数学公式检索文献,即使依据其他手段检索到含有目标数学公式的文献,当读者想验证或重新编辑这些数学公式时,也只能使用专门的数学公式输入插件,如MathType或数学排版软件LaTex,按照其语法规则重新输入.由于数学表达式除英文字符、阿拉伯数字和希腊字母之外,还包括许多特殊的、大小不一、形式各样的符号,这使其输入过程比较复杂,极大降低了相关领域知识共享与信息检索的效率,因此数学公式的自动识别越来越重要.
自1968 年Anderson[1]在其博士论文中首次提出公式识别问题以来,越来越多的学者参与到这一问题的研究中:Belaid等[2]使用从上到下和从下到上两个句法分析算术和三角函数方程的自动识别问题;Lee等[3]利用统计方法提出一个识别印刷体数学表达式的系统;我国学者肖建于等[4]提出基于凸壳和模糊识别的数学公式识别方法,该方法能明显提高字符空间关系判别的识别率,识别正确率可达93.5%;Maclean等[5]针对手写体数学公式,提出一种使用关系语法和模糊集解析二维输入的新方法;刘婷婷等[6]基于支持向量机的方法识别数学公式,识别正确率可达98%.
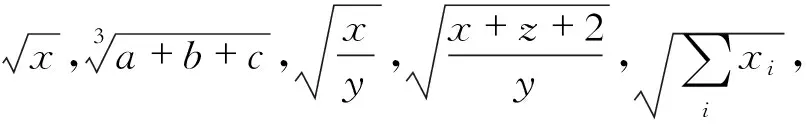
1 根号几何特征分析
字符识别通常采用比对算法,即将分割好的单字符与字模比对,取方差最小字模为识别结果.但此方法对根号的识别非常困难,这是因为根号长短不一、高低不同,难以用通常的比对方法进行识别.不同于手写数学公式,印刷体数学公式书写相对规范,几何特质明显,因此可考虑通过根号的几何特征来实现精准识别.
定义1设X为一个数学公式二值化图片,按照从上到下,从左到右的统计原则,第一个黑色像素点坐标(xup,yup)称为X的上角点,最后一个黑色像素点坐标(xdown,ydown)称为X的下角点.
图1给出3种数学公式二值化图片的上角点和下角点.类似地,可定义X的左角点和右角点.

图1 3种数学公式角点示意图Fig.1 Corner sketches of three kinds of mathematical formula
定义2设X为一个数学公式二值化图片,按照从左到右、从上到下的统计原则,第一个黑色像素点坐标(xleft,yleft)称为X的左角点,最后一个黑色像素点坐标(xright,yright)称为X的右角点.
定义3设X为一个数学公式二值化图片,(xup,yup)和(xdown,ydown)分别为X的上角点和下角点,假设xdown≤xup,如果对于任意x∈(xdown,xup),点(x,y)均为X的黑色像素点,其中
则称X拥有首一特征线.
对数学排版软件LaTeX中数学公式输入插件MathType的单字符集以及大小写、英文字母集进行统计,拥有首一特征线的字符集为{≠,*,,∀,∧,∨,⊄,Δ,,记为CandidateSet.显然仅通过判断数学公式二值化图像是否拥有首一特征线,不能唯一确定该数学公式中是否带有根号,必须增加新的判断规则.根据根号的几何特征,根号左角点和下角点之间距离严格大于零,即xdown-xleft>0.根据这一特征条件,CandidateSet减少为{≠,*,∀,∨,⊄,,
另外,根号的首一特征线的斜率为负,即
通过以上分析,可以根据数学公式二值化图像是否具有以下特征来唯一确定数学公式中是否存在根号:
1) 拥有斜率为负的首一特征线;
2) 左角点和下角点间距大于零;
3) 上角点所在水平线存在连续不间断黑色像素点.
2 根号次数确定
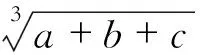
第1步,注意到公式中3与其附近的根号是完全分离的.实际上,它被夹在y=yup,y=yleft,x=xleft和x=xdown这4条直线之间,因此可以据此将3从根式中分离出来.
第2步,制作数字1~9字模用于比对,每个字模一般为一个N×N的0-1矩阵;
第3步,将切割好的3标准化为一个N×N矩阵,并与9个数字字模一一比对,方差最小字模所代表的数字,即根式次数.
3 算法设计与程序实现
基于Matlab开发语言,设计下面的算法.
第1步,读入数学公式图片,并将其二值化,二值化后的数学公式图片保存在矩阵A中.
第2步,根据印刷体数学公式的规范性,两个单字符间有一定的空白间隔.利用这一特性对矩阵A中每一列进行检测,若连续两列元素均为1,则可在这些列处对A进行切割,切割后矩阵记为B,其个数设为n.
第3步,对每个矩阵B(i),i=1,2,…,n,确定其上、下、左、右角点坐标.
第4步,对每个矩阵B(i),判断其是否拥有斜率为负的首一特征线,左下角点间距是否大于零,以及上角点所在水平线是否存在连续不间断黑色像素点,如果3个逻辑判断结果均为真,则断定B(i)中含有根号;否则断定B(i)中没有根号.
第5步,对含有根号字符的矩阵B(i),将夹在y=yup,y=yleft,x=xleft和x=xdown4条直线之间的部分切割出来,标准化后存放在临时矩阵BT中.
第6步,制作数字1~9字模,将BT与9个数字字模比对,记下方差最小字模所对应的数字,即为BT(i)的根号次数.
对于来自不同类型文档的200个公式截图,使用上述算法进行识别,所有公式中的根号全部正确识别,识别正确率达100%.使用Inter i5-3470 3.2 GHz处理器,2 GB内存,耗时5.845 s,其中200张公式截图读入时间为4.136 s,识别程序仅耗时1.709 s.
4 结 语
数学公式因其字符的复杂性,导致传统OCR技术无法对其进行有效识别.而根号又与其他数学字符大不相同,其长短、高低随着公式的不同有较大变化,识别难度较大.本文基于根号的几何特征,提出首一特征线的概念,并结合根号的其他几何特征,设计根号的识别算法,试验结果表明该算法有较高的识别率.
