基于lp-范数的ECT图像重建算法研究
2020-10-17孙美娟
马 敏,孙美娟,李 明
(中国民航大学 电子信息与自动化学院,天津 300300)
1 引 言
电容层析成像(electrical capacitance tomography, ECT)是上个世纪80年代发展起来的一种用于工业管道检测的过程层析成像技术。由于其快速、安全、非侵入、无损害的特点已被应用于气液两相流空隙率测量、流型识别、气固两相流浓度分布测量、航空发动机滑油检测等多个领域[1]。
ECT传感器系统主要有传感器阵列、数据采集单元和成像计算机3部分。在实际操作过程中,由于不同流体的介电常数不同,当流体通过传感器阵列时会引起极板间介电常数的改变,从而测量引起电容值的变化,采集单元进行电容值数据采集,然后将数据处理后传送到成像计算机。成像计算机再选择合适的成像算法完成图像重建[2]。
目前ECT图像重建算法可分为非迭代算法和迭代算法。非迭代算法主要有线性反投影算法、Tikhonov正则化算法等,其共同点是一步成像,图像重建速度快,但是重建精度不高。迭代算法主要有Landweber算法、共轭梯度算法等,其重建图像分辨率较好,但收敛速度较慢,实时性不佳。
2006年,Candes及其所在团队提出压缩感知的概念。该理论指出如果信号本身是稀疏的或者可压缩时,那么可以通过线性测量,对信号进行低维表示,因此可以获得比奈奎思特采样更少的采样数,并且能实现对原始信号的精确重构。该理论极大地降低了数据采集、存储及传输过程的压力,同时也极大地提高了信号处理效率[3]。
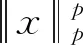
2 压缩感知基本原理
2.1 信号的稀疏表示
压缩感知理论认为只要信号是稀疏或者可压缩的,就可以经过某种线性观测,再利用重构算法从少量观测值中恢复出原始信号,不同于传统的信号采样,基于压缩感知理论的的信号处理方式将压缩与采样同时进行,采用这种方式会丢弃大量冗余或无用的信息,不仅提升了采集速度,更减少了信号存储和传输过程的压力。压缩感知信号处理过程如图1所示。

图1 压缩感知理论框架Fig.1 Theoretical framework of compressed sensing
根据压缩感知理论,压缩测量实际上是线性测量,通过观测矩阵对信号进行观测,因此观测矩阵的设计需要保证原始信息尽可能多的包含在观测值当中,这样才能保证原始信号由观测值精确地重构出来[4]。
假设长度为N的一维信号x∈RN,由信号稀疏理论可知,该信号可用一组正交向量基ψ=[ψ1,ψ2,ψ3,…,ψN]线性表示为[5]:
(1)
式中:ψi(i=1,2,3,…,N)为N维列向量;α为长度为N的一维向量;α中大部分系数为0或者接近0,且仅有K个非零元素,满足K≪N。此时信号x在正交基ψ下是稀疏的,稀疏系数为α,稀疏度为K。在压缩感知理论中,只要信号具有稀疏性或者在经过某种变换后变得稀疏,就可以把信号进行压缩。
常用的稀疏基有:离散Fourier变换基(DFT)、离散余弦变换基(DCT)、离散正弦变换基(DST)、离散小波变换基(DWT)等。
2.2 观测矩阵的设计
基于压缩感知理论的信号处理是通过观测矩阵进行信号的压缩与采样,因此需要设计一个随机观测矩阵φ∈RM×N(M≪N),观测矩阵和稀疏基不相关,信号的投影过程如下:
y=φx
(2)
式中:y∈RM×1,可以看出投影得到的向量维数远小于原始信号。将式(1)代入式(2),整个压缩感知过程可表示为:
y=φx=φψα=Acsα
(3)
式中:y为M×1维观测值向量;φ为M×N维观测矩阵;令Acs=φφ,称Acs为压缩感知矩阵。
对于给定的y从式(3)中求出x是一个线性规划问题,但由于M≪N,使得方程个数少于未知数的个数,故此方程为不定方程,通常无确定解。但如果原始信号x在某组基下的系数向量是稀疏的,则可以运用压缩感知理论求其确定解。文献[3]指出,当压缩感知矩阵Acs满足限制等距条件(restricted isometry property,简称RIP)时,系数向量α的K个非零系数便可以从M个测量值中准确恢复,从而保证重建算法收敛。然而判断给定矩阵Acs是否满足RIP性质是一个较为复杂的过程[6]。文献[7]指出,当观测矩阵和稀疏基不相关时,Acs可以在很大概率上满足RIP条件。
2.3 重构算法
最后就是信号的重构过程,对于式(3),矩阵Acs中列数大于行数,因此该线性方程有无数多个解[8],为了满足压缩感知理论信号稀疏性的前提,因此系数向量α应尽可能稀疏,该问题就变成一个系数向量尽可能稀疏的最优问题。理论证明,在测量矩阵满足限制等距条件时,原始信号可以通过下式优化问题进行重构[9]:
(4)
由于l0范数具有非凸性,使得直接求解式(4)的数值计算极不稳定而且是NP困难问题。Donoho和Chen等人指出,当观测矩阵和稀疏基不相关时,求解一个更加简单的最小l1范数问题可以得到同等的解:
(5)
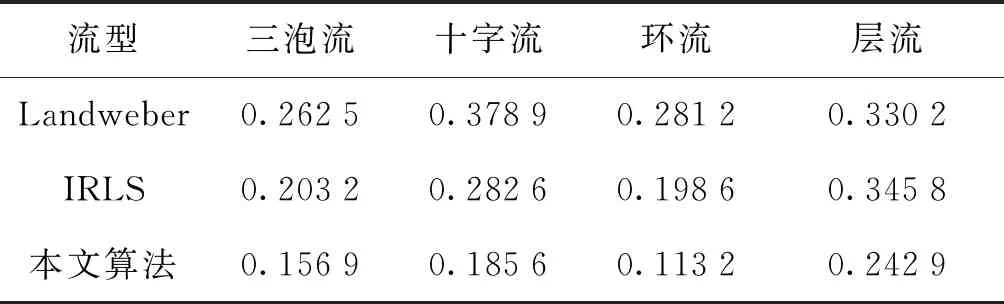
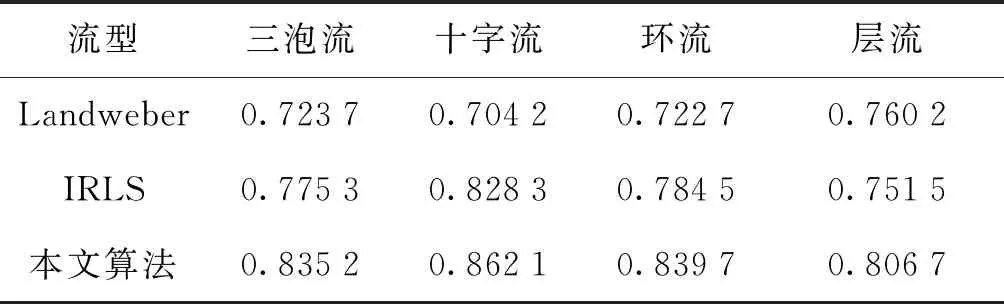
基于l1-范数的算法虽然重构效果好但计算复杂度高而且传输数据有较大冗余。文献[10]中进一步改进重构算法的性能,使压缩感知重构算法能更加具有一般性,提出基于lp(0 (6) CS理论要求观测系统对原始信号的观测过程为线性过程,ECT系统线性模型如下: C=SG (7) 式中:C为M×1维归一化电容测量值矩阵;G为N×1维的归一化介电常数分布矩阵,在图像重建过程中代表图像灰度值;S为M×N维矩阵,反映了电容C受物质分布变化G的影响,称为敏感场。 图2 离散余弦变换基稀疏效果Fig.2 Sparse effect of discrete cosine transform basis 在ECT系统中,原始信号为图像灰度信号,不具有稀疏性,根据压缩感知理论,必须对图像灰度信号进行稀疏化处理,使其满足压缩感知理论的前提,本文以典型的四泡流为例,分别使用常用的离散傅里叶变换基、余弦变换基、小波变换基、正弦变换基进行处理,结果表明离散余弦变换基稀疏效果较好,如图2所示。因此将离散余弦变换基作为ECT系统的稀疏基。 x=ψDCTα (8) 式中:x为N×1维图像灰度向量;ψDCT为N×N维离散余弦变换基;α为N×1的稀疏系数向量。 在ECT系统中,重建图像信号可以经过稀疏处理变得稀疏,但灵敏度矩阵S是否满足RIP难以判定。Donoho指出,如果观测矩阵的列向量独立性越强,则观测矩阵与稀疏基之间的非相关性就越强,从而压缩感知重构的效果越好[10];Szarek等证明了矩阵的列相关性与矩阵的最小奇异值相关,矩阵的最小奇异值越大,列向量间的独立性越强[11]。因此可以通过增大矩阵的最小奇异值来增加观测矩阵列向量之间的独立性,从而对观测矩阵进行优化。 SVD分解是将矩阵A分解为左奇异矩阵U、对角矩阵、右奇异矩阵V,表达式如下: A=U[Δ0]VT 式中:A为M×N维矩阵;U为M×M维正交矩阵;[Δ0]为M×N维对角矩阵;V为N×N维正交矩阵;Δ=diag(δ1,δ2,…,δM),δ1,δ2,…,δM为矩阵A的奇异值。 通过矩阵的奇异值分解将灵敏度矩阵进行分解,然后计算对角矩阵的奇异值的平均值,并将奇异值都赋值为平均值,处理方式如下,令: 式中:δmean为δ1,δ2,δ3…,δM的均值。 Snew=QUTS=[Δ*0]VT (10) 式中:S为未优化前的灵敏度矩阵; 相应的电容测量值也变换为: Cnew=QUTC (11) 变换后可得到新的ECT系统数学模型: Cnew=Snewg=SnewψDCTα=Acsα (12) 式中:Snew为优化后的M×N维系统观测矩阵;Cnew为M×1维的电容值向量;Acs为压缩感知矩阵。 近年来,在稀疏信号重建方面,随着非凸松弛方法的发展,许多学者证明了lp(0 (13) 式中:ε=(ε1,ε2,ε3,…εn),通过调整参数εi>0,可以得到 (14) 则 (15) 原来的最优化模型可以更改为: (16) 根据对新模型建立阈值表示,并提出改进的迭代阈值算法进行求解。 对于任意的参数λ>0,μ>0,α>0,令 易知,对于任意的μ>0,H2(x,x)=H1(x) 证明过程如下: ≥μH1(x*) =H2(x*,x*) (17) 式中:Bμ(x*)=x*+μAT(b-Ax*)。 证明过程如下: 由引理可得,令x*∈Rn为式(17)的解,则: (18) 式中:[Bμ(x*)]i为向量Bμ(x*)的第i项。 结合阈值表示理论,用于求解式(17)的迭代阈值算法可以被定义为: =sign([Bμ(xk)]i)· (19) 通常对于正则化模型,图像的重建质量取决于正则化参数的选取,然而人工选择合适的参数非常困难,因此本文选用自适应的方法进行参数的选取,令x*为模型的最优解,稀疏度为r,假设 |[Bμ(x*)]1|≥|[Bμ(x*)]2|≥ …≥|[Bμ(x*)]n|, 根据式(19)有以下不等式: 可得: 则令: (20) 在本文中,通过自适应的方法来选择最优参数,使得p值能够根据输入参数自动确定其大小,为了使p值收敛敏感定义相对误差: 则: rRMSEk=rRMSEk-rRMSEk-1 最终p值的更新为: (21) 式中:β为步长,通过这种方法可以有效求解式(16)。 为了验证范数值p取不同时对重构率的影响,固定的观测矩阵A∈R120×3 228,随机生成稀疏向量x0,通过Ax0=b得到向量b,通过本文算法求解原始信号x0,实验取Tol=10-5,β=1。由于该算法对参数ε的依赖性较强,这里设置εi=max{0.7|[μAT(b-Axk)]i|,10-3}。定义重构率为原始信号和重构信号之间的相关系数。同时为验证该算法在ECT图像重建过程中p值的选取对重建结果的影响,选取三泡流、四泡流两种流型进行不同p值时的图像重建。 图3 不同p值及稀疏度时的重构率Fig.2 Reconstruction rate with different p values and sparsity 由图3所示,显示了不同p值时,本文算法对不同稀疏度信号的重构能力,比较不同p值时算法的重构能力,可知当稀疏度为[0,40]时,p=0.7的重构效果较好,当稀疏度为[40,80]时,p=0.1的重构效果较好,当稀疏度为[80,95]时,p=0.9的重构效果较好,由表1可知,四泡流中,p=0.7时的重建效果伪影较少图像较清晰,而三泡流中,p=0.3时图像质量较好,目标位置轮廓准确。综上可知p值的选取影响着最终的重构效果。 表1不同p值重建结果 为验证本文提出的自适应与之迭代算法的重构效果,本组实验选取三泡流、十字流、环流、层流4个相对复杂的流型进行仿真实验,选取Landweber算法、IRLS算法进行仿真实验对比,重建结果如表2所示,图像重建速度、图像相对误差、图像相关系数如表3、表4、表5所示。 表2 不同算法重建结果Tab.2 Reconstruction results with different algorithm 表3 图像重建速度比较Tab.3 Image reconstruction speed comparison s 表4 图像相对误差Tab.4 Image relative error 表5 图像相关系数Tab.5 Image correlation coefficient 由仿真实验结果可以看出,本文提出的自适应阈值迭代算法在成像质量上,相对于Landweber迭代算法有明显提升,三泡流粘连情况得到改善,目标位置、轮廓较为清晰;十字流成像结果虽然未完全反映原始流型信息,但是改进算法可以明显辨别出目标的形状;改善最为明显的是环流,边缘效应的影响减少,且伪影较少,目标轮廓明显,从数据反应看,图像误差得到了很好的控制。在成像速度方面,由于算法引入了阈值表示理论,在计算量方面得到了很好的改善,成像速度也得到了明显提高。 (1) 本文在分析ECT不定问题的基础上,提出将压缩感知理论应用到ECT的图像重建中去。仿真实验表明,基于压缩感知的ECT图像重建算法能够利用少量数据实现ECT图像的精确重构。 (2) 针对取不同值时,对随机生成数据及三泡流、四泡流的重构结果的成像质量进行比较。实验表明,基于lp(0 (3) 本文提出的基于lp(03 基于自适应阈值迭代的ECT图像重建
3.1 稀疏基的选取
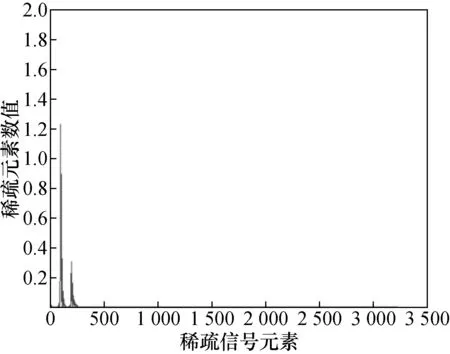
3.2 基于SVD的观测矩阵优化
3.3 自适应阈值迭代算法
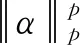

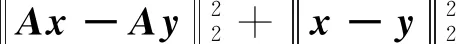

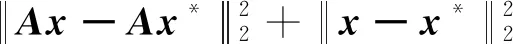

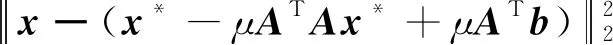

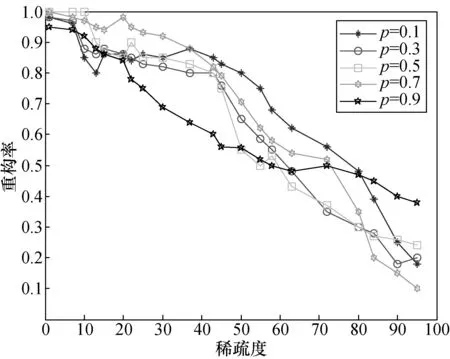
4 仿真实验
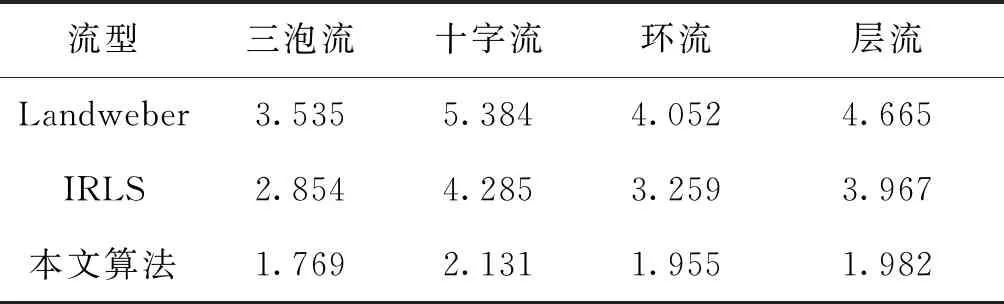
Tab.1Reconstruction results with different value

5 结 论
