相容性单木生物量模型估计方法的比较*——以青冈栎为例

刘秀红 姜春前 徐 睿 何 潇 齐梦娟

(1. 中国林业科学研究院林业研究所 国家林业和草原局林木培育重点实验室 北京 100091； 2. 中国林业科学研究院资源信息研究所 北京 100091)

在林木及森林生物量估算中，单木生物量模型是一种高精度高效的方法。其不仅可以准确评价林分现实生长，也可以预估未来林分生长，有助于定量研究林木生长过程，可为经营措施的制定及实施提供依据(Patriciaetal.， 2008； 彭娓等， 2018； 王维枫等， 2008)。

目前，生物量模型估测法是计算生物量比较常用的方法，它是利用林分易测因子如胸径、树高、冠长、冠幅等来推算难以测定的林分生物量(彭小勇等， 2007； 黄贤松等， 2011)。此外，异速生长关系W=aXb(W为因变量，X为自变量，a、b为待估参数)经常被用于生物量模型拟合(韩文轩等， 2008； 张宇等， 2016； 杨宪龙等， 2016； 苏瑞兰， 2017； 刘坤等， 2017)。这类简单的异速生长方程只需要基本的森林调查数据，就可以估算出生物量，预测精度较高(Bietal.， 2010； Castedodoradoetal.， 2012； Gonzálezetal.， 2013； Paréetal.， 2013)。在建立生物量模型时，如果各组分生物量模型是独立拟合的，则会存在模型之间不相容的问题，即分项生物量预测值之和不等于总生物量的预测值。为解决此问题，许多研究者(Tangetal.， 2001； Parresoletal.， 2001； Bietal.， 2004； 曾伟生等， 2011； 曾伟生， 2012)提出了联立方程组的方法，并使用不同的结构形式建立相容性生物量模型(Tangetal.， 2001； Bietal.， 2004； Dongetal.， 2015)。为保证各分项生物量模型估计结果的相容性，目前国内外有多种形式的相容性生物量模型(Merinoetal.， 2006； 曾伟生， 2011； 曾伟生等， 2011a; 2011b; 2011c； Lietal.， 2013； Dongetal.， 2015； 董利虎等， 2015a； 2015b； 2016； 彭娓等， 2016)，在模型构建方法上，目前除了比例总量直接控制法，代数和控制法也被更多研究者使用，如刘薇祎等(2018)利用比例总量直接控制及代数和控制2种方案建立不同地域的马尾松(Pinusmassoniana)相容性生物量模型； 马克西等(2018)利用比例控制和代数和控制建立了新疆云杉(Piceaspp.)一体化立木生物量模型。符利勇等(2014)比较了常见的3种方法： 非线性似然无关回归方法(Parresol， 2001； Bietal.， 2004)、比例平差法(唐守正等， 2000)和线性或非线性联合估计方法(骆期邦等， 1999)，发现比例总量直接控制生物量模型的预测精度最高。

生物量模型的参数估计算法常使用最小二乘法(李海奎等， 2012； 黄兴召等,2017； 郑冬梅等,2018)，而最小二乘法又分为普通最小二乘法(OLS)、二阶最小二乘法(2SLS)和三阶最小二乘法(3SLS)。OLS在单个方程参数的估计中应用广泛，但用OLS单独去估计每个方程的参数而不考虑方程组中的其他方程时，势必忽略方程组间的相关关系，用此算法估计的参数有偏，而且是非一致的(杜沔等， 2014； 周海川， 2017)。2SLS和3SLS均适用于恰好识别以及过度识别的结构方程。由于联立方程模型中每个随机方程之间往往存在某种相关性，表现在不同方程的随机误差项之间，因此，如果采用2SLS估计方法分析将忽视这种相关性，造成信息损失。3SLS属于系统估计方法，该方法考虑了模型系统中不同结构方程随机误差项之间的相关性，可同时估计联立方程中的所有参数，比2SLS逐个估计每个方程更为有效(李树生， 2008； 周海川， 2017)。鉴于生物量模型构建方法不同会影响模型参数及评价指标(刘薇祎等， 2018； 马克西等， 2018)，且参数估计算法不同也会使模型参数及评价指标存在差异(Ritchieetal.， 2008)，目前还缺少有关方法的比较。

为此，本研究基于25株青冈栎(Cyclobalanopsisglauca)的地上生物量实测数据，分别使用OLS、2SLS及3SLS作为模型参数估计算法，建立比例总量直接控制、代数和控制2种结构形式的相容性生物量模型，共6种方案，做对比评价，以期选择出最好的生物量模型构建方法及参数估计算法，为生物量的模型计算和研究提供技术支撑。

1 研究区概况

采样地点为湖南慈利县二坊坪天心阁林场(111°07′—111°15′E，29°12′—29°16′N)，该区属中亚热带季风湿润气候，土壤以黄红壤为主，土壤有机质层大约厚20 cm，土层较薄，岩石以变质页岩、砂页岩为主。林场内物种资源丰富，现有木本植物667种，属87科215属。

天心阁林场前身为村集体林地，由于林农经营管理较粗放，导致林分质量不高，但在整个林区没有开矿、毁林开垦和大型放牧等破坏森林活动。在1988年建林场后，通过封山育林的方式，使退化森林逐渐恢复成青冈栎次生林，林分郁闭度高。

2 研究方法

2.1 样地设置与调查 参照《生态系统固碳观测与调查技术规范》， 2018年5—6月在天心阁林场选取立地条件基本一致的林分，在同一坡向、坡位，利用罗盘仪分别建立9个1 000的青冈栎天然次生林样地。对样地内胸径≥5 cm的乔木每木检尺和挂牌，记录种名、胸径和树高，并计数每个树种在不同样地的个体数量。

2.2 解析木伐取与分析 按胸径划分为6、8、10、12、14、16和18 cm共7个径阶，每径阶选取2～5株标准木伐倒，共25株样木。采用单株伐倒法取样，分别称量树干、树枝和树叶的鲜质量，由于研究样地分布于黄石水库，为避免破坏森林对水土保持的维护能力，未对样地内的样木进行挖根。同时截取基部圆盘读取年龄。

分别取树干、树枝、树叶150 g鲜样带回实验室，于85 ℃烘箱内烘至恒质量，称干质量，然后计算各组分干质量(生物量)。

生物量建模样本信息见表2。

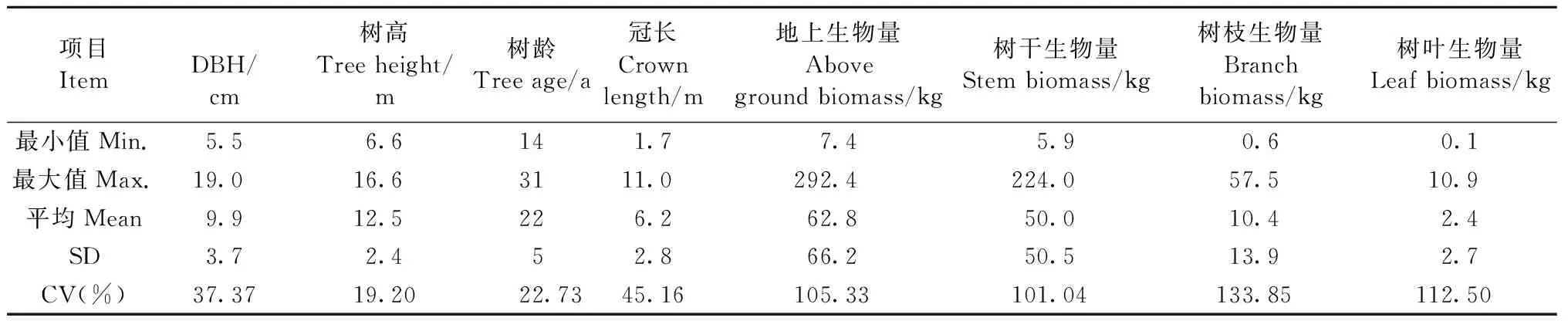
表2 建模样本统计信息Tab.2 Information statistics of modeling samples

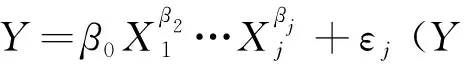
2) 生物量模型的建立 (1)传统独立模型 各组分实际观测数据直接拟合各项生物量的参数，即各组分之间生物量的估计都是独立进行的。形式如下：

Wi=fi(xi)+εi, (i=1,…,4)，

即为：Wi=aDb+εi,(i=1,…,4)。

式中：Wi为单株各组分生物量，fi(xi)为各组分独立回归模型；xi为模型自变量；ε1～ε4为各项随机误差。

(2)比例总量直接控制模型 该模型可以直接计算出地上部分的生物量模型，再由地上部分直接平差分配给树干、树枝、树叶。对各组分进行联合建模，模型中参数通过联立方程组法求解得到。形式如下：

W1=f1(x)+ε1；

式中：W1，W2，W3和W4分别为单株地上、树干、树枝和树叶的生物量(kg)，f1(x)，f2(x)，f3(x)，f4(x)分别为地上、树干、树枝和树叶的生物量模型；x为自变量。

化简并代入aDb后，方程组为：

W1=a0Da1+ε1

式中：a0、a1、b0、b1、c0、c1为模型参数。

3)代数和控制模型 该模型是计算出树干、树枝、树叶部分的模型后，3部分模型相加得到地上部分生物量模型，即各组分生物量与地上部分生物量联立成方程组，各组分的回归方程包含自身的自变量，而地上部分的生物量是所有自变量的函数之和，以此来保证各组分之和等于总量，模型形式如下：

W1=f2(x)+f3(x)+f4(x)+ε1；

W2=f2(x)+ε2；

W3=f3(x)+ε3；

W4=f4(x)+ε4。

代入aDb后模型形式如下：

W1=a2Db2+a3Db3+a4Db4+ε1；

W2=a2Db2+ε2；

W3=a3Db3+ε3；

W4=a4Db4+ε4。

式中：a2、b2、a3、b3、a4、b4为模型参数。

2.4 生物量模型估计算法 1)普通最小二乘法OLS 所建立的回归模型使所有观察值的残差平方和达到最小的一种估计算法。

2)二阶段最小二乘法2SLS 首先在OLS估计下产生一个工具变量，之后通过工具变量法得出一致估计的结构参数。2SLS使用了模型中的一部分信息，忽视了模型结构对其他方程参数值所施加的全部约束条件(李建明等， 2011)。

3)三阶段最小二乘法3SLS 应用2SLS的估计误差构造模型随机扰动项协方差矩阵的统计量，从而对整个模型进行广义最小二乘估计。3SLS是联立方程模型的一种完全信息估计方法，利用所有可用的信息，同时估计模型中的所有方程。在一定条件下比两阶段最小二乘估计具有更好的渐近有效性(张仲礼等， 2008)。

2.6 生物量模型评价 采用6项指标评价生物量模型，分别为确定系数(R2)、估计值的标准误(SEE)、总相对误差(TRE)、平均系统误差(ASE)、平均估计误差(MPE)和平均百分标准误差(MPSE)(曾伟生等,2011)：

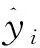
普通最小二乘法(OLS)、二阶最小二乘法(2SLS)以及三阶最小二乘法(3SLS)估计算法均在R软件systemfit包中实现，对上述2种相容性生物量模型进行非线性联合估计，即nlsystemfit，加权回归拟合参数，计算6项评价指标。

关于样本数据是否需要划分为建模数据和检验数据，仍是个有争议的问题(Kozaketal.， 2003； 曾伟生等， 2011c)。Beak(1984)和Shao(1993)认为仅使用建模数据所计算出的评价指标来评价模型的预估能力无法使人信服； 曹磊等(2018)和曾伟生等(1999)也认为单独采集一套检验样本进行适用性检验的做法不可取，应该利用全部样本来建立模型。本研究为了充分利用样本信息，不区分建模样本和检验样本，即将建模样本全部作为检验样本使用，用上述评价指标对模型进行评价。

3 结果与分析

3.1 青冈栎独立模型参数估计以及模型评价 地上以及各组分生物量独立生物量模型的参数及评价指标见表2。除树叶外，其余组分的确定系数都在0.92以上，以地上部分生物量模型的拟合效果最好，R2达0.97； 分项生物量模型中，树干生物量模型拟合效果最好，R2达0.95； 树枝生物量模型其次，R2达0.92； 树叶生物量模型最差，但R2也达0.84以上。拟合精度表现为地上>树干>树枝>树叶。

3.2 比例总量直接控制相容性模型 基于不同参数估计算法所得比例总量直接控制相容性模型的参数见表3。使用OLS作为估计算法时，与独立生物量模型地上组分计算的参数较为一致，而与2SLS和3SLS估计算法计算的模型参数有差别。另外，除b0和b1外，使用2SLS和3SLS估计算法所得的生物量模型参数基本一致，两者与OLS估计算法所得的估计参数差别较大。

表2 独立模型拟合结果以及评价指标Tab.2 Fitting results and evaluation indexes of independent model

表3 比例总量直接控制模型拟合结果Tab.3 Fitting results of controlling directly by proportion functions

基于不同参数估计算法所得比例总量直接控制相容性模型的评价指标见表4—6，在3种不同参数估计算法下，各组分评价指标略有差异。对于干、枝、叶以及地上组分来说，OLS估计算法下TRE明显偏小一些，甚至接近于0，除此之外，OLS、2SLS和3SLS估计算法下的其他评价指标相差不大。在同一参数估计算法下，拟合精度都表现为地上>树干>树枝>树叶，这与独立模型评价下的模型精度相一致。综合而言，对于比例总量直接控制相容性模型，OLS参数估计算法略优于2SLS和3SLS。

3.3 代数和控制相容性模型 基于不同参数估计算法所得代数和控制相容性生物量模型的参数见表7。使用2SLS和3SLS估计方法所得的生物量模型参数基本一致，两者与OLS估计算法所得的估计参数差别较大。在OLS估计算法下，a2、b2与独立模型树干组分的预估参数更接近，a3、b3、a4、b4与独立模型树枝、树叶组分的预估参数差别也不大，独立模型估计参数与2SLS、3SLS估计算法下的估计参数差别较大。

基于不同参数估计算法所得的代数和控制相容性模型的评价指标见表4—6。2SLS和3SLS估计算法下的评价指标基本一致。对于树干、树叶和地上组分来说，使用OLS作为估计算法，其R2偏大且ASE、MPE、MPSE、SEE和TRE偏小，明显优于2SLS和3SLS估计算法。对于树枝来说，使用OLS估计算法所得的R2更大一些，且ASE、MPE、SEE和TRE偏小，只有MPSE略大于2SLS和3SLS，预估效果也要优于2SLS和3SLS估计算法。综合而言，对于代数和控制相容性模型，使用OLS估计算法要优于2SLS和3SLS。

3.4 最优模型构建方法的选择 表4—6分别为比例总量直接控制法、代数和控制法在不同估计算法下的评价指标。以估计算法OLS为例，无论是树干、树枝、树叶还是地上组分，除比例总量直接控制下的总相对误差TRE较小外，2种估计方法下的其余评价指标十分接近，没有明显的差异。可见，OLS估计算法下，2种模型构建方法拟合效果相差不大。同理，在2SLS与3SLS算法下，比例总量直接控制的确定系数R2略大，ASE略小，但其TRE也要偏大，另外3项评价指标没有明显差异。综合来说，2种模型构建方法拟合效果也相差不大。

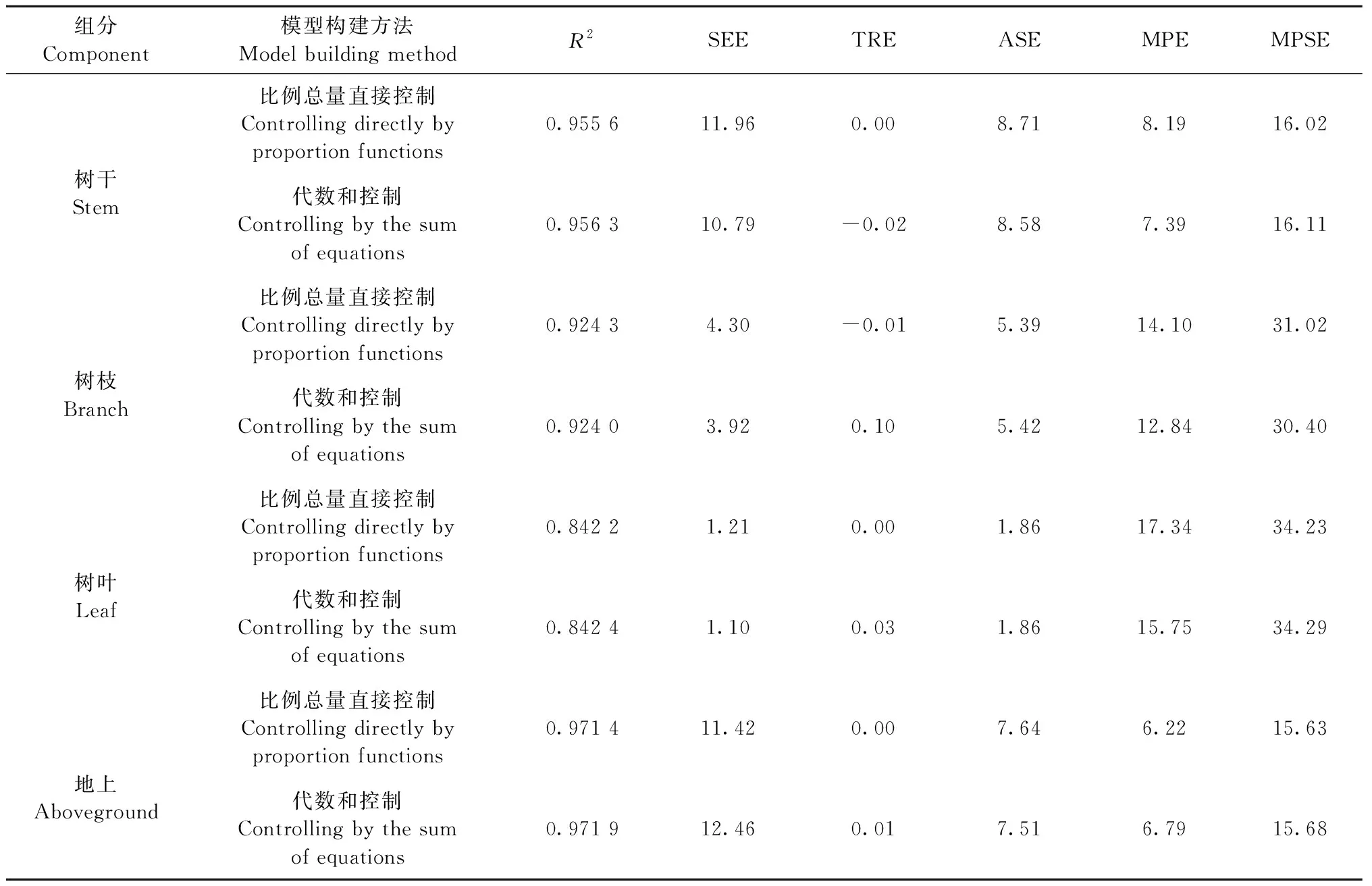
表4 OLS估计算法下的评价指标Tab.4 Evaluation indexes of OLS

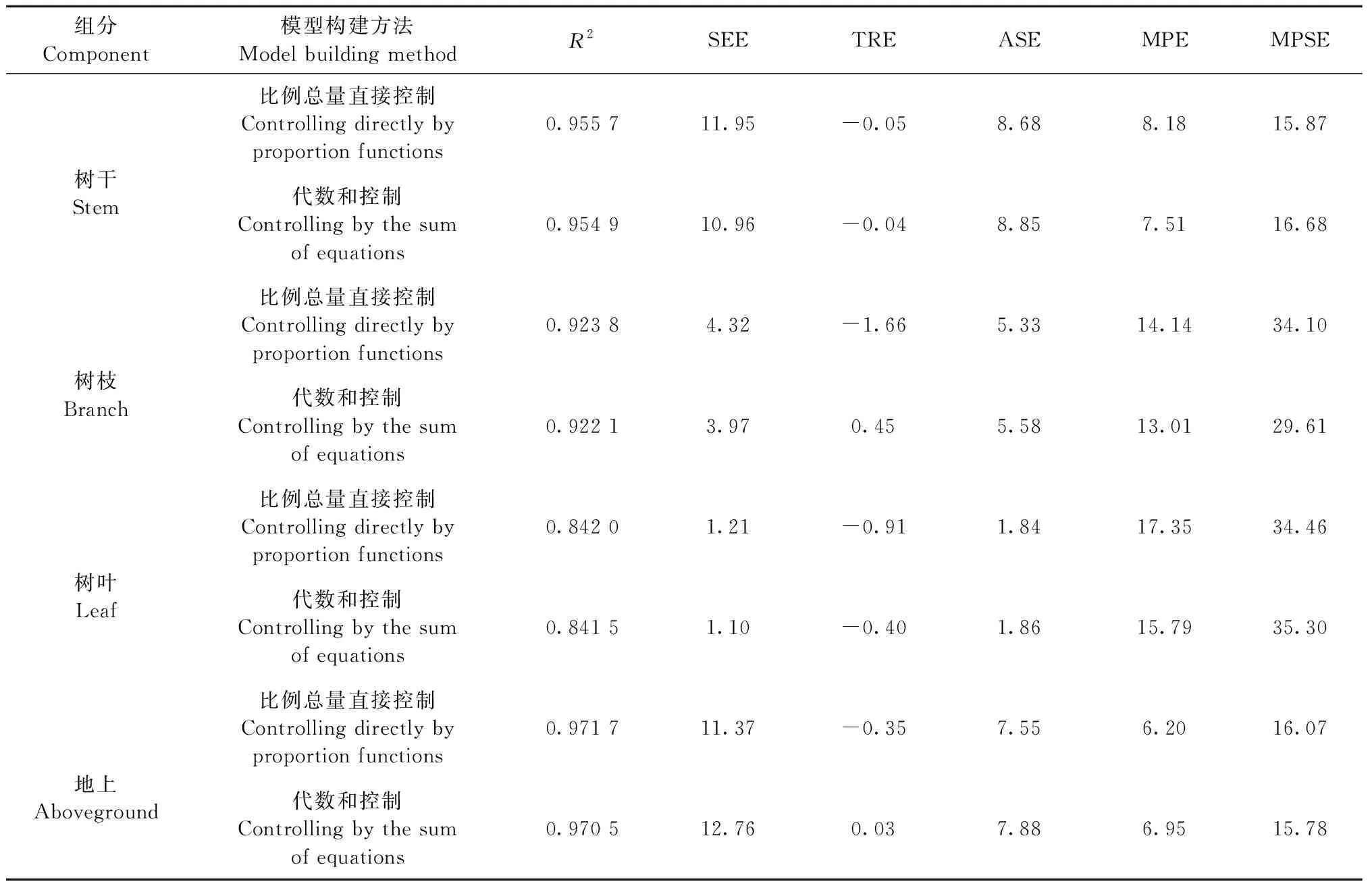
表5 2SLS估计算法下的评价指标Tab.5 Evaluation indexes of 2SLS

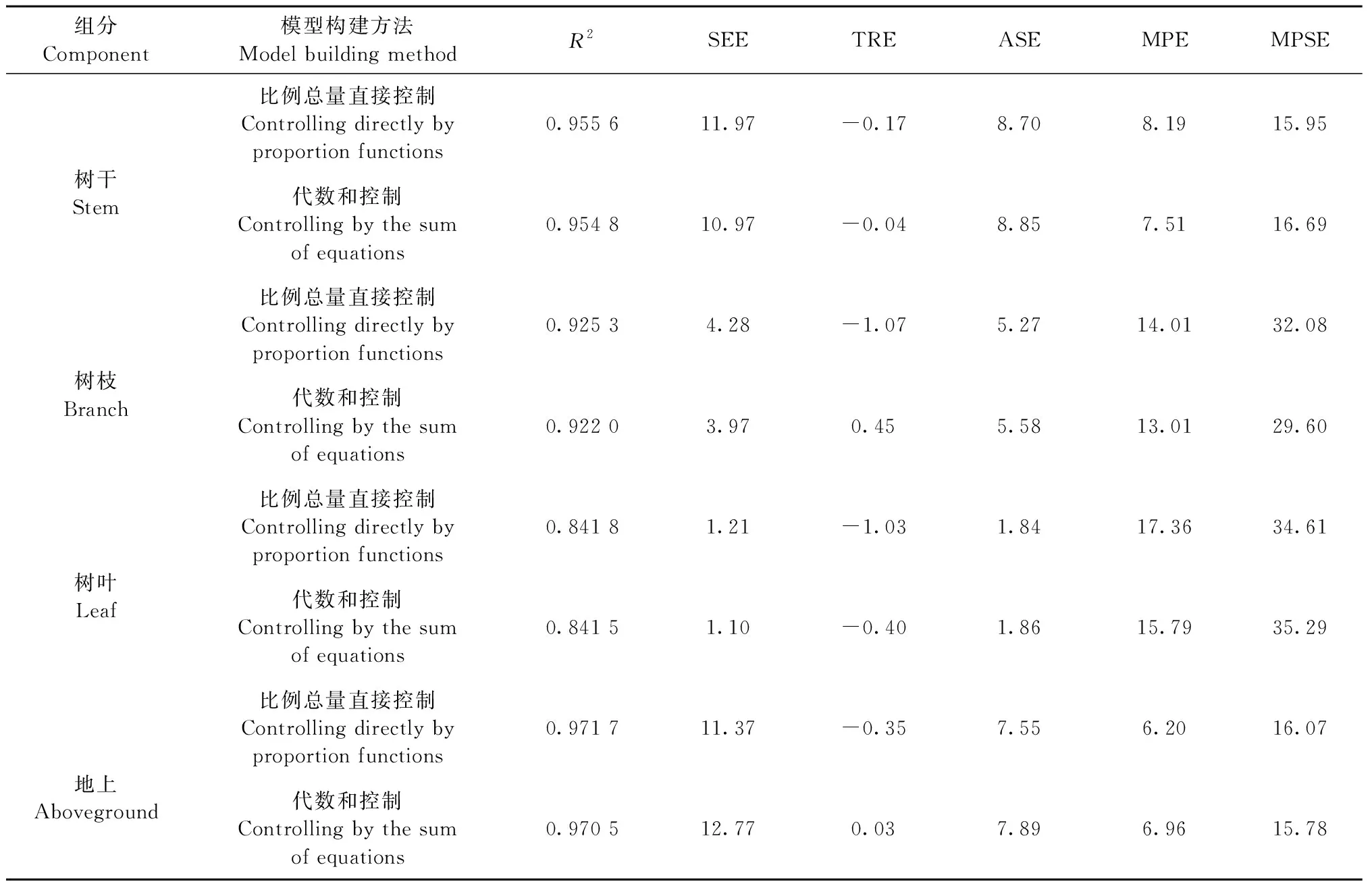
表6 3SLS估计算法下的评价指标Tab.6 Evaluation indexes of 3SLS

表7 代数和控制拟合结果Tab.7 Fitting results of controlling by the sum of equations

4 讨论

本研究以青冈栎为对象，分别以OLS、2SLS和3SLS为参数估计算法，使用比例总量直接控制和代数和控制2种结构形式的相容性生物量模型，建立了地上、树干、树枝和树叶4个组分的相容性生物量方程。比例总量直接控制和代数和控制相容性模型皆是非线性联合(唐守正等， 2000)估计的结果，是在保持各组分之间兼容的前提下(曹磊等， 2018； 骆期邦等， 1999)估计参数。对地上生物量模型而言，比例总量直接控制生物量模型的参数与独立生物量模型基本一致； 对各组分生物量模型而言，代数和控制生物量模型的参数与独立生物量模型基本一致。这些结果与以往研究一致(邢海涛等， 2017； 陈振雄等， 2018)。

在不同参数估计算法下，参数估计以及评价指标有较大差异(李树生， 2008)。本研究表明，无论是比例总量直接控制生物量模型还是代数和控制生物量模型，在2SLS和3SLS估计算法下的参数与评价指标差异性较小甚至接近一致，而与OLS的估计算法所得的参数与评价指标有较大差异。这是因为OLS仅仅对模型中的每一个解释变量与工具变量做回归，未利用单方程外的信息(杜沔等， 2014； 周海川， 2017)，而2SLS分2个阶段进行，首先解释变量对工具变量进行回归，得到解释变量的拟合值，之后得到的解释变量拟合值对被解释变量进行回归，即为2SLS的回归结果，2SLS只使用了模型的一部分信息(范德成， 2000； 赵娜等， 2018)。3SLS使用了模型的全部信息(刘盛， 2007； Hasenaueretal.， 1998)，是以2阶段估计误差构造扰动项方差的统计量，进行广义最小二乘估计，是2SLS的逻辑推广。本研究使用的2种生物量模型自变量少，且仅有4个方程联立，使用2SLS和3SLS估计算法时，比例总量直接控制和代数和控制估计的结果较为一致； 2SLS和3SLS每个结构方程往往是过度识别的，这就要求大样本容量，但是在单木生物量模型研究中，并没有理论意义上的“大样本”，对小样本估计特性进行比较更有实际意义。从理论上讲，在小样本情况下，各种估计算法的估计量都是有偏的。在生物量模型研究中，OLS作为参数估计算法已经获得了很好的估计效果，过多考虑模型信息反而会降低模型精度。同时3种参数估计算法在给予合理初始值时，拟合难度表现为3SLS>2SLS>OLS，因此OLS作为参数估计算法是最优选择。

比例总量直接控制生物量模型以及代数和控制生物量模型都满足了林分总生物量等于各分项生物量之和这一逻辑关系(刘薇祎等， 2018； 马克西等， 2018)，且均符合地上总生物量预估效果最好、树干和树枝生物量次之、树叶生物量预估效果最差的结论。在同一参数估计算法下，2种模型构建方法对各组分生物量的拟合效果基本相当。比例总量直接控制方法首先计算出的是整体生物量，在全株或者地上生物量计算中更为方便快捷，即总量模型简单； 而代数和控制生物量模型首先计算树干、树枝、树叶等组分生物量，然后相加得到地上或者全株生物量。在林业实践中，多以获得全株或地上生物量为目标(董玉峰等， 2015)，因此选择比例总量直接控制生物量模型更有实践意义。

5 结论

在OLS、2SLS和3SLS这3种参数估计算法中，生物量模型的估计参数及评价指标有明显差异，综合考虑模型精度、小样本特性及数据拟合难度，认为OLS是生物量模型最优的参数估计算法。比例总量直接控制和代数和控制这2种结构的生物量模型均可很好地解决独立生物量模型中不相容的问题，两者的拟合精度都较高，但比例总量直接控制相容性模型在获取整株生物量时计算简便。在林业生产中，建议使用OLS参数估计算法下的比例总量直接控制生物量模型来计算各组分生物量。