基于CFD法的螺旋溜槽内二次环流分布特性研究

高淑玲，孟令国，魏德洲，宋振国，袁 俊

(1.东北大学资源与土木工程学院，辽宁 沈阳 110819；2.矿冶科技集团有限公司，北京 100160)

在众多重选设备中，螺旋溜槽凭借结构简单、分矿清楚、功耗低等优点而倍受关注[1-3]。螺旋溜槽良好的分离性能得益于其独特的流场特性[4]。矿浆流入螺旋溜槽后，一方面沿槽面向下作螺旋运动，此为主流；另一方面在过水断面内作回转运动，形成横向二次环流[5]。二次环流的存在可引起螺旋溜槽内矿浆的循环，同时促使下部流层中的重矿物和上部流层中的轻矿物分别向内缘和外缘移动，从而起到加速分带和提高分离精度的作用[6]。因此，通过强化二次环流分选作用从而提高螺旋溜槽的分离性能，是对螺旋溜槽结构和操作参数优化的重要途径。

在理论研究层面，由于纵向主流和横向二次环流之间具有一定的交互作用，同时螺旋溜槽又具有多流态并存的特征，因此直接对二次环流进行理论建模较为困难。为简化研究，卢继美[7]曾假设主流对二次环流没有影响，推导出不同流态下横向流速的理论公式，在此基础上，徐镜潜等[8]又推导了离心螺旋溜槽正转和反转时的横向流速理论公式，并提出了离心惯性力增减与二次环流速度变化的对应关系。随后，黄尚安等[9]利用量级比较法推导了螺旋溜槽层流区域的横向流速公式，认为横向流速与表面切向流速、螺旋线曲率半径、液膜厚度以及槽面宽度均有关。HOLTHAM[10]则基于层流和湍流速度公式预估了螺旋溜槽中的横向流速值，但其假设缺乏有效数据验证，数据的合理性还需要进一步考量。以上研究为揭示螺旋溜槽内二次环流的作用奠定了基础，但由于不同理论模型所侧重的机理和螺旋溜槽的几何结构不同，因此造成这些理论模型的普适性和准确性均不理想。

早期对螺旋溜槽流场参数的测试多采用荧光微丝法和染料注射法等传统手段[9,11]，这在一定程度上证明了横向二次环流的存在，然而却无法对横向流速进行定量表征。随着现代测试技术的发展，黄秀挺[12]利用激光多普勒测速仪(LDA)考察了螺旋溜槽入口流量对横向流速特性的影响，发现入口流量与二次环流的强弱及分界点位置密切相关，这些研究结果为定量分析螺旋溜槽内的横向流速特性提供了重要参考。

采用计算流体力学方法(computational fluid dynamics，CFD)对螺旋溜槽流场进行模拟计算是当前流场研究的另一个重要手段[13-14]。WANG等[15]构建了一套适于螺旋溜槽模拟的螺旋坐标系统，较为系统地研究了螺旋溜槽内的水流特性，但受当时计算条件的限制，模拟过程中将流体流态假定为层流，同时将螺旋溜槽断面形状简化为矩形，因此模拟工况与实际偏差较大。在此基础上，MATTHEWS等[16]对模拟方法进行改进和优化，采用VOF多相流模型和RNGk-ε湍流模型成功捕捉到了气液自由表面和二次环流等重要流体特征，但外缘处的横向流速模拟值与PIV测试值相差较大，推测这可能是由于外缘较高的湍流强度导致空气夹带，从而造成PIV测量误差，同时数值模拟方法也有待于进一步优化。

值得注意的是，螺旋溜槽内的流体呈现为一种无压的薄膜流动，因此网格质量以及湍流模型等因素对计算精度均会产生影响。在上述研究背景下，本文采用CFD数值计算方法对螺旋流槽中的横向流速特性进行系统研究，通过考察不同数值条件对横向流速模拟结果的影响，确定适于螺旋溜槽中水流特性的模拟方法，进而查明二次环流在螺旋溜槽内的空间分布特性，为揭示其作用机理奠定基础。

1 模拟策略

1.1 螺旋溜槽流场模型构建

利用Solidworks软件建立螺旋溜槽几何模型，其中螺旋溜槽的断面形状为立方抛物线，直径为300 mm，螺距为240 mm，圈数为5圈。通过ICEM软件对螺旋溜槽内流体域进行网格划分，对网格数量及底壁网格尺寸进行优化研究，所考察的网格数量包括357 000、429 590和522 410，底壁网格尺寸分别为1 mm和2 mm。螺旋溜槽的几何模型及其计算域的网格划分如图1所示。

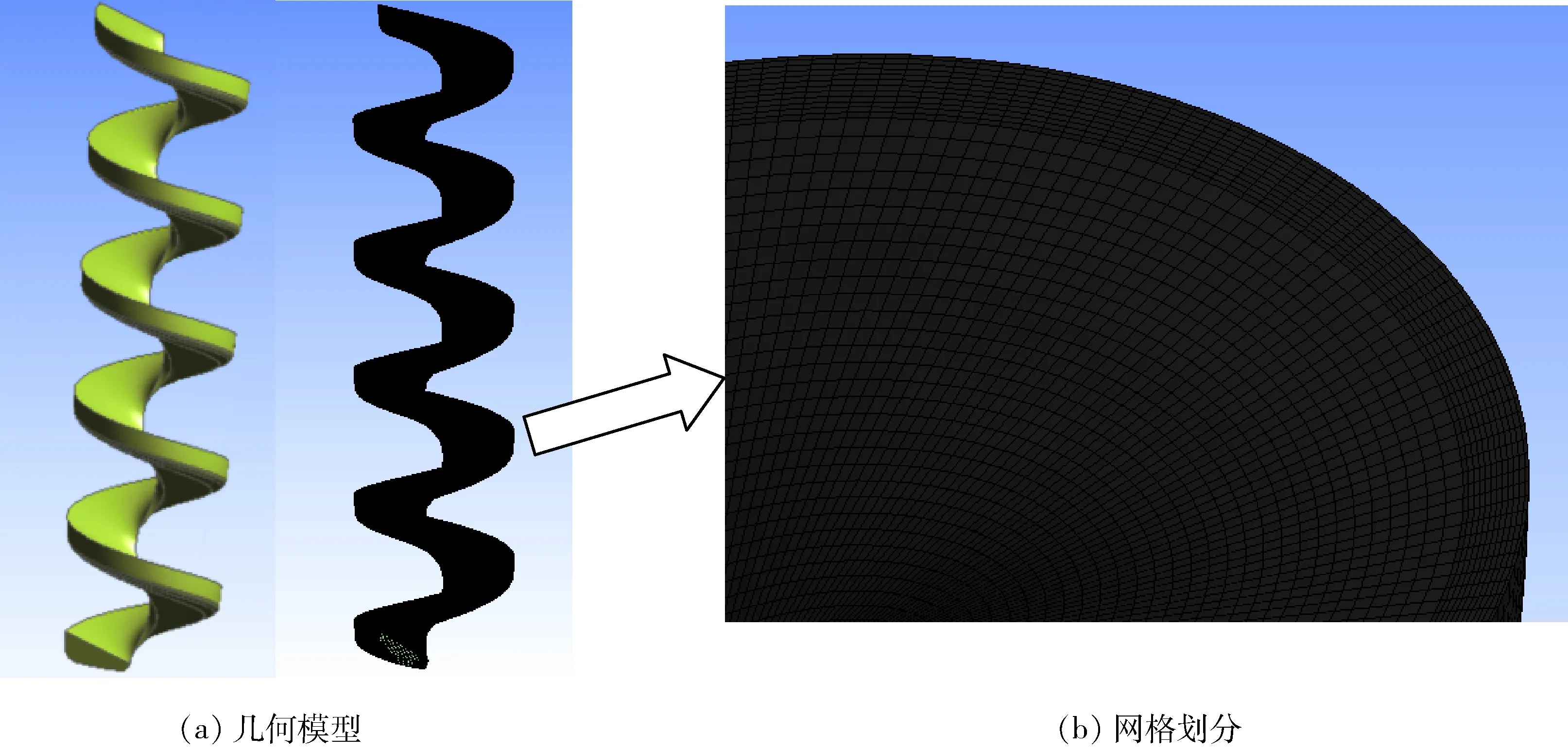
图1 螺旋溜槽几何模型及网格划分Fig.1 The geometric model and mesh of spirals

1.2 边界条件设置

模拟所采用的入口条件为速度入口，入口速度为入口流量与入口面积的比值，本文所采用的入口流量均为8 L/min。螺旋溜槽排料端与大气相通，设为压力出口，空气的回流体积分数设为1，水相的回流系数设为0。 螺旋溜槽计算域中的上表面、下表面均设为无滑移壁面，壁面函数采用标准壁面函数。

1.3 模型选择

由于螺旋溜槽中的流体流动属于开放的薄膜流，水与空气之间存在明显界面，因此采用VOF多相流模型捕捉气液表面，主相设置为水，次相设置为空气。选取合适的湍流模型有利于提高计算结果的可靠性和精确度，本文所考察的湍流模型分别为标准k-ε模型、RNGk-ε模型和RSM模型。

1.4 求解参数及收敛标准

本文采用的求解控制算法为压力-速度耦合SIMPLE算法，压力离散格式采用PRESTO格式，对动量、动能、湍动能扩散率等均采用具有二阶精度的Second Order Upwind离散格式。在迭代计算过程中，各个物理变量的收敛残差标准均设定为1×10-3。

2 模拟结果与分析

2.1 网格数量对螺旋溜槽横向流速分布特性的影响

采用标准k-ε湍流模型对3种网格数量(357 000、429 590和522 410)的螺旋溜槽流场分别进行数值模拟，得到第3圈末槽面内不同径向位置的横向流速沿水深分布曲线，如图2所示。在此需要说明的是，由于不同径向位置处的流膜厚度不同，因此采用相对水深(h/H)表征流体质点的水深位置，其中:h为某一流体质点与槽底的垂直距离；H为同一径向位置处的水面与槽底的垂直距离，即该径向位置的流膜厚度。

从图2中可以看出，网格数量对横向流速沿水深的分布特征具有明显影响。在径向134 mm和138 mm处，当网格数量为357 000时，液流全部向外缘流动，流速沿水深方向逐渐增大；当网格数量增至429 590和522 410时，上部液流(较大水深处)向外缘流动，下部液流(较小水深处)向内缘流动，以相对水深h/H=0.50～0.66处为分界点，此处流速为0；在径向142 mm处，3种网格数量下模拟出的横向流速均在相对水深h/H=0.30～0.35处出现分界点，相比而言，网格数较少时的二次环流强度较弱一些；在径向位置145 mm处，3种模拟条件下的二次环流特性均未出现。上述分析表明，网格数量划分为429 590和522 410时模拟出的横向流速分布比较合理，可以更为准确地捕捉螺旋溜槽内横向二次环流的流动特性。

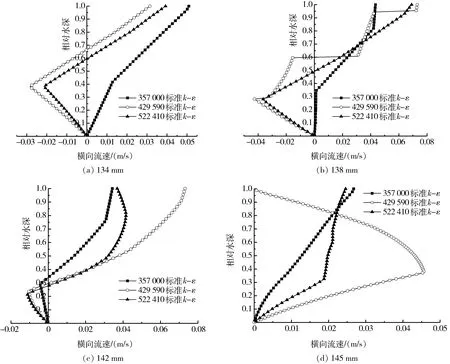
图2 不同网格数量下各径向位置处的横向流速沿水深分布图Fig.2 Radial velocity distribution diagram under different mesh numbers

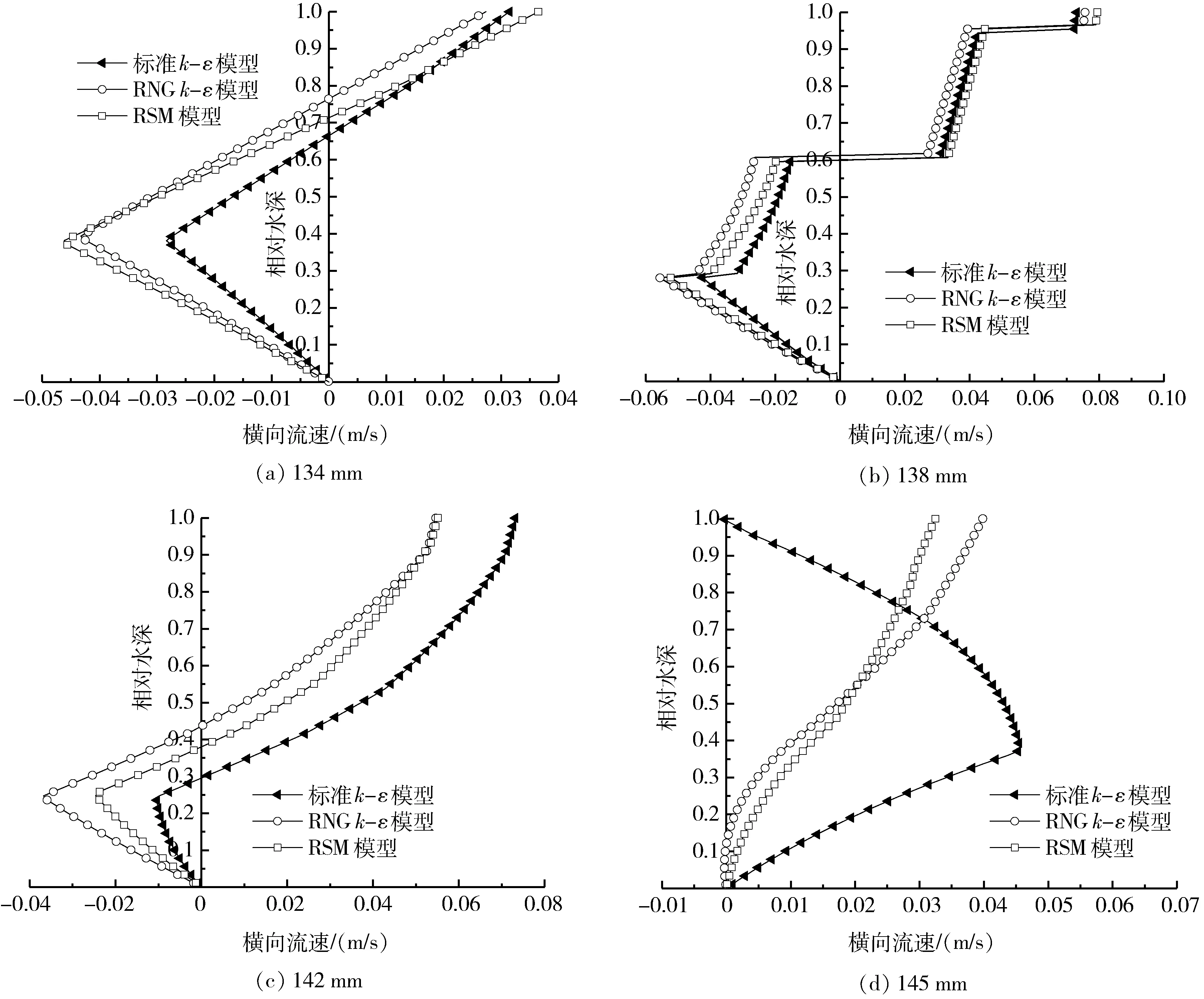
图3 在网格数量为429 590的条件下采取不同湍流模型所得横向流速沿水深分布图Fig.3 Radial velocity distribution diagram with different turbulence models under the mesh number of 429 590

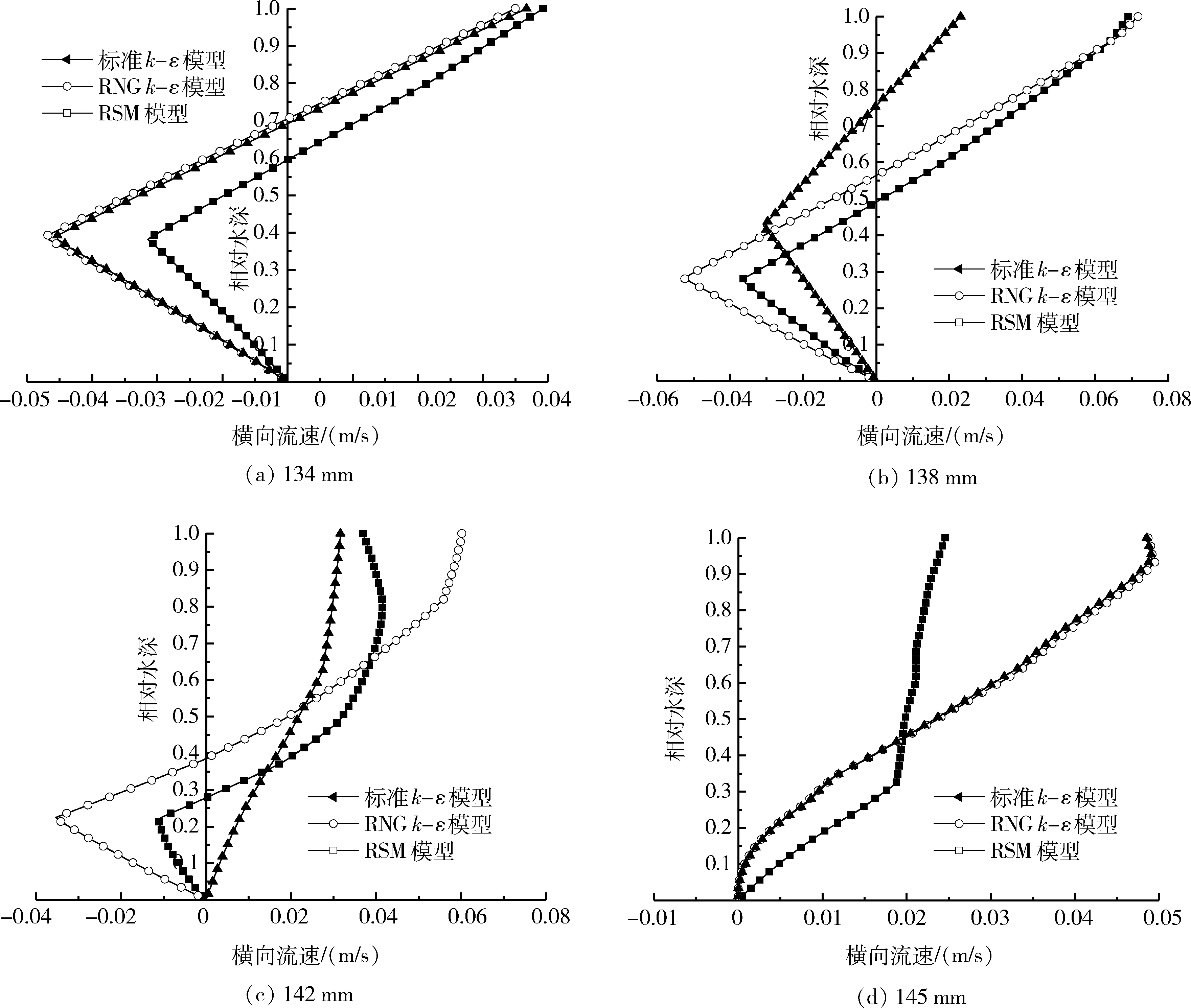
图4 在网格数量为522 410的条件下采取不同湍流模型所得横向流速沿水深分布图Fig.4 Radial velocity distribution diagram with different turbulence models under the mesh number of 522 410

2.2 湍流模型对螺旋溜槽横向流速分布特性的影响

在网格数量为429 590和522 410的条件下，分别采取标准k-ε、RNGk-ε和RSM湍流模型对螺旋溜槽内流场进行模拟，得到第3圈末槽面中不同径向位置处的横向流速沿水深分布曲线，如图3和图4所示。

观察图3可以看出，在径向位置134 mm和142 mm处，采用不同湍流模型时，上部水流的横向流速均随着相对水深增加而增大，采用标准k-ε模型时模拟出的二次环流作用比在另外两种湍流模型下的作用要弱些；而在径向位置138 mm处，横向流速曲线出现多个拐点，且在一定的相对水深范围内没有发生改变，表明当网格数量为429 590时，采用3种湍流模型所得的模拟数据与二次环流理论特征吻合度均较差；在径向位置为145 mm处，标准k-ε模型下的横向流速随着相对水深的增大先增大而后减小，这也与流速理论特征不符。

由图4可知，将网格数量增为522 410时，在径向位置为134 mm处，不同湍流模型下的横向流速都是随着相对水深的增加而增大，同样是在标准k-ε模型下模拟出的二次环流作用比另两种湍流模型下的作用更弱；流体径向位置外移到138 mm时，采用标准k-ε模型和RNGk-ε模型所得到的横向流速增大，符合回转流的流动原理，而采用RSM模型所得的横向流速反而减小，这一点与流动原理不符；在径向位置142 mm处，采用RSM模型时并没有捕捉到二次环流作用；在径向位置145 mm处，采用标准k-ε模型所得到的横向流速从相对水深h/H=0.3开始向上呈现陡增趋势，当采用RNGk-ε模型和RSM模型时，横向流速随相对水深增加而渐次增大，只在水流表面处略有减小，这是由表面气相阻力和边壁效应所致，因此这一模拟结果与实际水流特性是一致的。

以上结果表明，在网格数量为522 410的条件下，采用RNGk-ε湍流模型模拟出的不同径向位置的横向流速分布趋势更稳定，与开放体系回转流的流动特性更为相符。

2.3 底壁网格尺寸对螺旋溜槽横向流速分布特性的影响

在上述优化试验条件下，进一步对比底壁网格尺寸(1 mm和2 mm)对螺旋溜槽流场计算结果的影响，获得第3圈末槽面内不同径向位置的横向流速沿水深分布曲线如图5所示。

从图5可以发现，在径向位置135 mm和142 mm处，两种底壁网格尺寸下的横向流速模拟结果差异不大，而在径向位置138 mm处，当底壁网格尺寸设为1 mm时，横向流速在相对水深h/H=0.6附近出现了较大的速度梯度，这并不符合流速连续分布特征，推测这是在采用标准壁面函数时加密计算网格所导致的计算结果失真。在径向位置146 mm处的水层表面，采用2 mm底壁网格所模拟出的横向流速值呈略减趋势，这是由于受到表面气相阻力和边壁效应的影响，故符合流体力学原理。综合模拟计算的稳定性和准确性，采用尺寸为2 mm的底壁网格更为适宜。

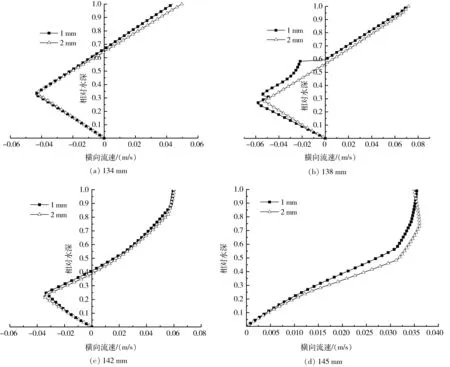
图5 采用不同底壁网格尺寸时横向流速沿水深分布图
Fig.5 Radial velocity distribution diagram by different bottom wall mesh sizes

2.4 螺旋溜槽内横向流速空间分布特性

根据上述研究结果，确定适宜的螺旋溜槽流场数值试验条件为：网格数量522 410、RNGk-ε湍流模型、底壁网格尺寸2 mm。在此基础上，对圈数为5圈的螺旋溜槽内的水流场进行了模拟研究，提取此数值条件下各圈末槽面内不同径向位置的横向流速计算值，各分布曲线如图6所示。

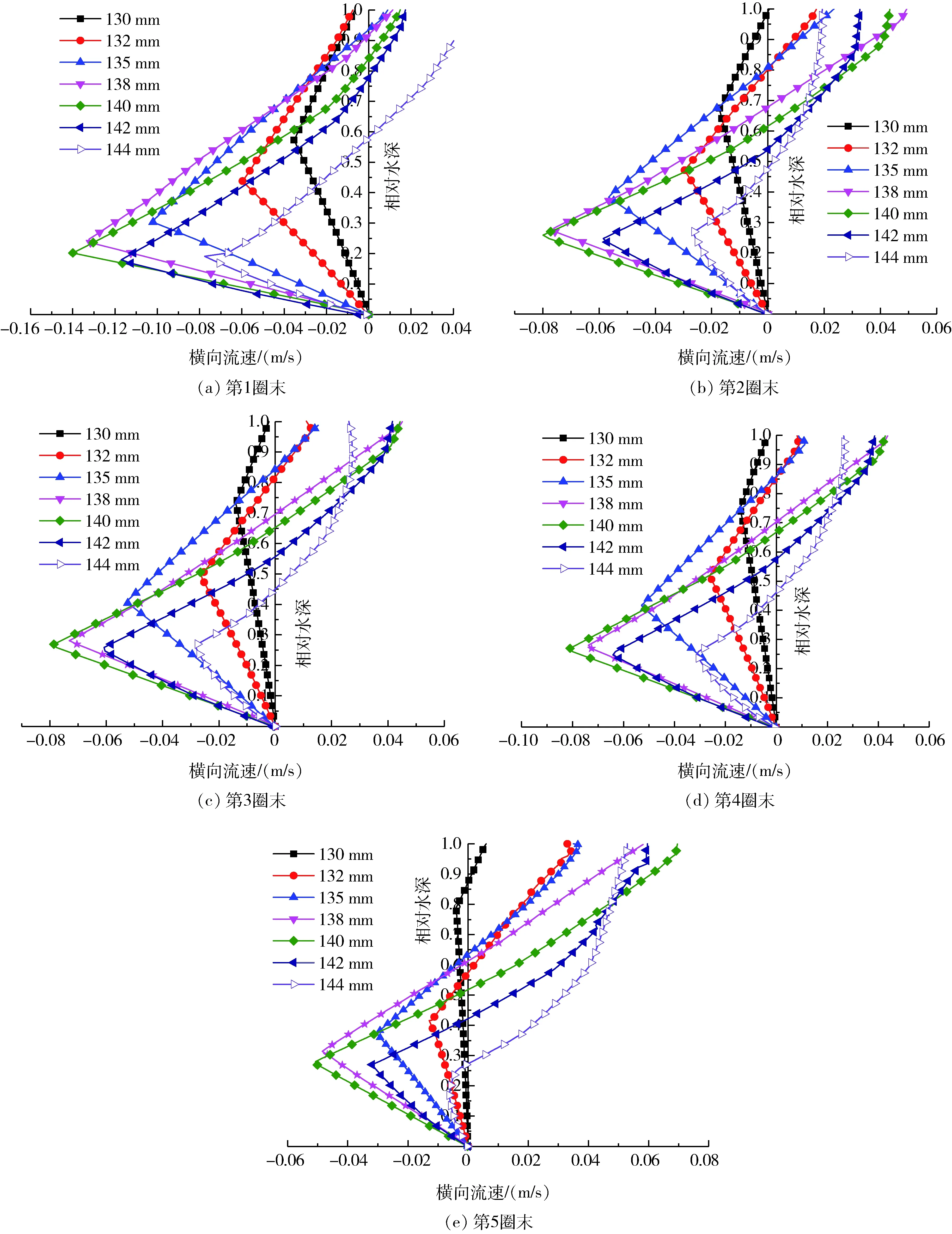
图6 各圈末槽面内不同径向位置水流横向流速沿水深分布图Fig.6 Radial velocity distribution diagram at different radial position of the end of each turn

从图6中可以看出，螺旋溜槽内水流的横向流速沿水深分布特性为，在某一水深位置存在分界点(内外流速转向点，此处速度为0)，符合上部液流向外流动、下部液流向内流动的二次环流特性，上部液流速度在水层表面达到最大值，下部液流则大致在流层中部达到最大值。横向流速分界点和下部液流最大流速值点与液流的过流圈数及径向位置密切相关，流速空间分布特性也随之改变。

具体来看，在第1圈末槽面内，各径向位置的横向流速分界点所处水深位置较高，且下部流体的横向速度绝对值明显大于上部流体的横向速度，表明此时水流向内缘运动趋势较强而向外流动较弱，尚未形成稳定的二次环流。这是因为，流体在刚进入槽内时初速度较小，回转运动所产生的离心力不足以克服重力沿槽面的分力作用，因此流体运动以向内流动为主，此时内缘区域的流膜厚度会相应增大，这对促进固体颗粒的松散与分层是非常有利的。

当流体继续运动到第2圈末槽面内时，各径向位置的横向流速分界点位置均下移，并且下部流体的横向流速明显减小，上部流体的横向流速则相应增加。这表明，随着流体向下加速流动，主流切向速度及其离心惯性力不断增大，从而加强了流体向外缘流动的趋势，而向内缘运动趋势被减弱，由此形成了较为稳定的横向二次环流。随过流圈数的进一步增多，流体受到的离心力进一步增强，横向流速分界点的水深位置进一步下降，即向内流动的下部流层边界收缩，这可在一定程度上减小低密度颗粒进入内缘的机率，有利于提高螺旋溜槽內缘产物的品级。另一方面，随过流圈数增多，下部液流达到最大流速的相对水深位置上移，而其所达到的流速最大值减小，预示着下层液流向内流动的速度梯度不断降低，表明流体流过第2圈及以后，横向流速沿水深分布特性愈加稳定。

在横向二次环流形成后的每一圈末槽面内，随径向位置外移，横向流速分界点所处的水深位置渐次下降，二次环流亦为内薄外厚的形态；表面流体质点达到的最大向外速度呈现先增大后降低的整体变化趋势，速度变化的拐点位于径向138 mm(第2～4圈末)和140 mm(第5圈末)两个相邻位置，并且这两处的流速非常接近，由此可将其视为横向流速缓变区；下部流体向内流动的最大速度也是出现在138 mm(第2圈末)和140 mm(第3～5圈末)两处，即二次环流作用最强区，距离螺旋溜槽外缘端点10 mm左右，自此向外，由于边壁阻流作用流速显著降低，二次环流作用被削弱。

3 结 论

1) 流体域网格划分数量和湍流模型对螺旋溜槽内横向流速模拟结果影响显著，而底壁网格尺寸对其影响较小。采用522 410个网格、RNGk-ε湍流模型和2 mm的底壁网格时，获得了符合斜面水流运动特性的数值计算结果。

2) 在螺旋溜槽第1圈末槽面内，流体以向内流动为主，随过流圈数增多，液流受到的离心惯性力增大，流体向外运动速度升高，由此形成了明显的二次环流；过流圈数增多同时使横向流速分界点位置下移，上下流层分流比例发生变化，下部流体达到的最大流速值变小，而对应水深位置上移，故流速梯度降低，横向流速沿水深分布特性愈加稳定。

3) 在二次环流形成后的各圈槽面内，随径向位置外移，横向流速分界点位置下降，二次环流轮廓呈现内薄外厚形态；表面流体质点的最大向外速度呈现先增大后降低的变化趋势，大致在螺旋溜槽外缘端点以内10 mm处存在速度变化拐点，亦为横向流速缓变区和二次环流作用最强区。