基于LCOE和性能罚款的海外IPP风电项目EPC竞标分析
2020-10-16王东
文 | 王东
可再生能源发电技术进步和成本降低等因素极大地推动了全球能源结构的调整。作为可再生能源的重要组成部分,风能的开发正在全球范围内进入快车道。据国际能源署(IEA)预测,2050年,风能在全球能源结构中约占1/3。随着技术进步,竞价风电项目越来越多,尤其是在海外市场。海外可再生能源的投资以独立发电者(IPP)为主,在中国“一带一路”倡议和“走出去”战略的推动下,国内许多大型电力企业积极参与IPP开发商的设计采购施工总承包商(EPC)项目竞标。对于该类项目,由于电价已通过购电协议(PPA)锁定,所以,生命周期内的平准化度电成本越低,其收益就越高。因此,IPP开发商在选择电站的EPC总承包商时,核心的评价标准是平准化度电成本(LCOE)。
本文结合LCOE和性能罚款,通过LCOE降低一个百分点所付出的代价来衡量投标方案。在合理的成本和风险边界内,具有最低LCOE降低代价的方案即为最佳方案。
LCOE用于风电项目EPC竞标的意义
2018年5月,我国风电竞价上网政策出台后,LCOE也火了。LCOE的核心算法是收入的净现值等于成本的净现值,常见的计算方法可参考美国Sunpower公司于2008年发布的算法:
平准化度电成本=(初始投资-生命周期内因折旧导致的税费减免的现值-固定资产残值的现值+生命周期内因项目运营导致的成本的现值)/生命周期内发电量的现值
由此可知,LCOE主要由建设成本、运维成本和发电量以及折现率决定。建设成本和发电量由EPC承包商的方案决定,运维成本取决于运维管理水平。如EPC承包商同时负责运维服务,那么,在同一税收、贷款比例和利率、折现率等财务数据的情况下,LCOE体现的是EPC承包商风电机组的选型、风电场的设计和运维管理水平。因此,用LCOE比较不同EPC方案的优劣,能直观反映不同风电机组的竞争力和方案降本增效的效果。
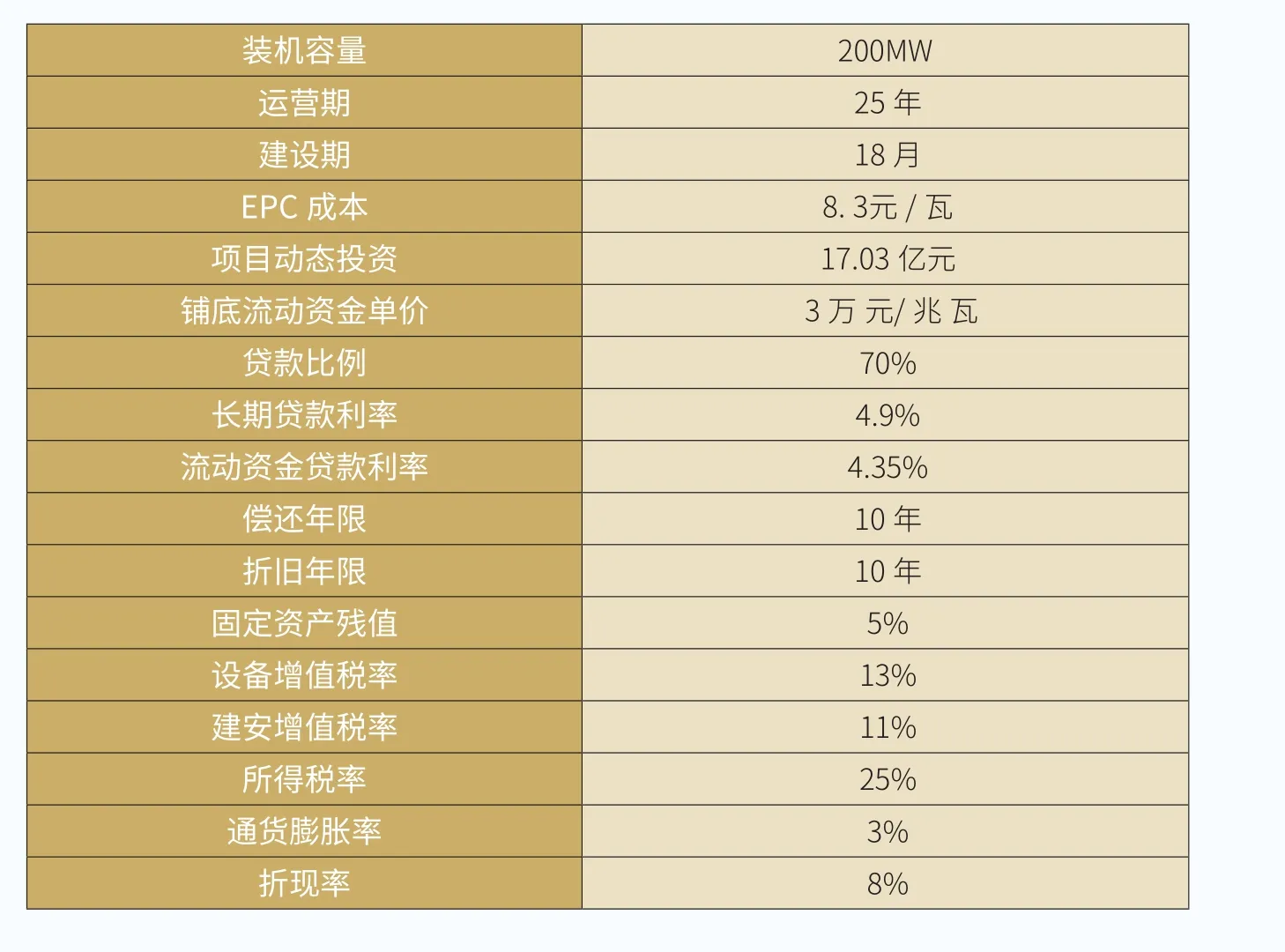
表1 LCOE输入条件
LCOE在风电项目EPC竞标中的应用
以某海外新能源IPP开发商开发的200MW风电项目为例。该项目场址交通状况良好,地势平坦,风能资源非常丰富,可达300W/m2。项目EPC方案的评标原则为LCOE最低。
项目的前期费用和土地租赁或购买的费用由IPP开发商承担,因此,不同EPC承包商投标方案LCOE的差异就是EPC成本和发电量的差异。为了针对性地做好投标工作,本文从LCOE的角度分析投标方案的优化方向,提高方案的竞争力。
一、LCOE的基本假设及LCOE变化分析
假设某项目的LCOE基本输入条件如表1所示,其中,税率、贷款比例、利率等财务输入条件是基于假设给出的。
首先分析建设成本、运维成本和发电量三个变量的敏感性。由图1可知,发电量对LCOE的影响最大,建设成本次之,运维成本最小。倘若运维由业主负责,或所有EPC承包商的运维报价基本相同,对于EPC承包商来说,只需考虑发电量和建设成本即可。
为分析建设成本和发电量同时变化时LCOE的变化情况,将LCOE的变化率定义为:
式中,LCOE'为当建设成本和发电量变化时,算出的新平准化度电成本;LCOEo为当建设成本和发电量为初始值时,算出的平准化度电成本。
让建设成本和发电量分别从90%以1%的步长增加到110%,绘制出图2。图中中间分界线处LCOE的变化率为0,表达式为y=0.74x(x为建设成本变化率,y为发电量变化率)。
LCOE变化率0线左上方区域的LCOE变化率为负,说明LCOE相比初始值降低;LCOE变化率0线右下方区域的LCOE变化率为正,说明LCOE相比初始值增加。当改变表1 中的假设条件时,y=0.74x仍然成立,图2的形状不发生改变。
由以上结论可知,为了增加EPC方案的竞争力,就要降低LCOE,即把当前方案在图2上的位置(0,0)向左上方移动。
二、LCOE的优化策略
一般EPC招标会有多个承包商参与投标。为简化分析,此处假设有两个EPC:EPC-A和EPC-B。对于多个EPC的情况,分析方法相同。
假设EPC-A和EPC-B在发电量和成本方面的竞争力分析如表2所示。
把EPC-A(0,0)和EPC-B(-0.05,0.02)两个点描绘在图2上,并增加一条过EPC-B点平行于LCOE变化率0线的平行线,如图3所示。
如果要使EPC-A的LCOE低于EPC-B,那么,EPC-A的点应在过EPC-B点的LCOE变化率0线平行线的左上方区域。实际上,风电机组的性能是有限的,发电量不可能大幅度提升,因此,本文将发电量的提升幅度限制在0~3%;成本优化的范围限制在-15%~0。

表2 EPC-A和EPC-B的发电量和EPC成本
让EPC-A的LCOE变化率相比EPC-B降低1%,那么,EPC-A目标点就在图3所示的目标线y=0.74x+0.076上。
三、结合性能罚款的优化策略
提高发电量,有可能导致性能罚款。假设项目保证的是功率曲线,功率曲线违约金定义如下(其中,不含税上网电价设为0.35元/千瓦时):
功率曲线的违约金=保证的年发电量×(功率曲线保证值-全场功率曲线考核值)×不含税上网电价×运营期
由图3可知,对于同一LCOE,存在不同的发电量和建设成本组合。为了更好地衡量LCOE降低所付出的代价,引入LCOE降低价值指标来衡量建设成本和发电量在LCOE每变化一个百分点时付出的总价值,定义如下:
设定上式取值如下:
(1)发电量变化率大于0时,相当于发电量有风险,这时有性能罚款(为负值);发电量变化率小于0时,性能罚款为零。
(2)建设成本增加,为正值;建设成本减少,为负值。
建立 LCOE降低价值(VoLC)最低的目标函数:
约束条件:
式中,CAPX为建设成本;AEPg为担保的发电量;P为电价;OPt为运营期;x为建设成本变化率;y为发电量变化率。
采用非线性GPR方法求解,可得最优解 x=-0.103,y= 0,VoLC=2557。即建设成本降低10.3%,发电量不变时,能以最小的代价达到LCOE降低的目标。
结论
不管是在国内无补贴的平价和竞价风电项目开发中,还是在海外IPP风电项目的EPC竞标中,都可以从LCOE的角度优化方案。通过本文分析可知,影响风电场LCOE的因素从大到小依次为发电量、建设成本、运维成本。通过发电量和建设成本双变量分析LCOE的相对变化规律,可实现EPC方案的优化。结合性能罚款的要求,找出达到LCOE优化目标代价最低的发电量和建设成本组合,有利于提升EPC方案的竞争力。
