立足经验 “理学”融通

王卉

【摘要】本文以一个课例的三个片段来阐述基于基本经验学情之下如何理清儿童的现实经验和思维过程，以促进计算教学中算理和算法间的相互融通，让学习历程看得见、说得清。

【关键词】基本经验 “理学” 思维过程

以学为中心的课堂，教师应从儿童的视角出发，以儿童现有知识和经验作为教学的起点，适时引导儿童依据先前习得的知识经验自主解决问题，充分展示学情材料、思维过程和个性化问题并逐步理清、理明。

一、立足经验，理出起点层次

小数乘整数是小数乘法单元中的起始内容，通过这部分内容的教学，一方面要使学生初步感受小数乘法的运算意义，积累探索和计算小数乘法的基本经验，并为进一步学习小数乘小数提供支持;另一方面则要使学生进一步体会数学前后知识之间的内在联系，感受数学的严谨性，培养初步的推理能力。学生学习整个基础知识的经验主要有三个：一是整数乘法的计算方法，二是小数的意义和性质，三是小数加法的计算方法。

基于这样的认识，教师课前利用十分钟让学生完成以下任务：想一个你喜欢的小数，通过写一写或画一画把它表达出来，让同学们猜一猜。

展示如下：

儿童的世界丰富多彩，换一种方式让“复习”回到课堂，呈现焕然一新的面貌。此环节目的是回顾小数的意义，为探究算理算法做铺垫。学生个性化的作品呈现出三种层次：一是把小数与读音和图画相联系进行创造;二是数学本质中小数是十进制分数的直观表达;三是对小数意义内化后的再创造。原先学生觉得“不接地气”的小数意义变得鲜活起来，也会让后面生僻枯燥的计算算理“鲜活”起来，细微的变化展现出别样的风景。

二、立足经验。理出方法多元

出示例题图：

尝试列式并口算出得数。

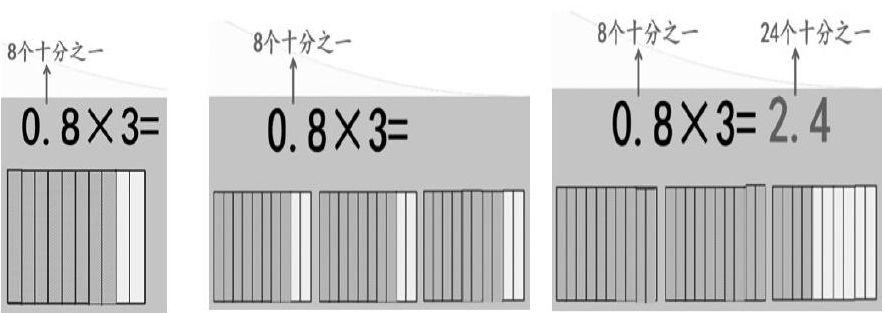
生1：0.8×3表示3个0.8相加;1.2×4表示4个1.2相加。

生2：0.8×3，先算8×3=24，再点小数点是2.4;1.2×4，先算12×4=48，再点小数点是4.8。

师：把0.8×3看成8×3，把1.2×4看成12×4来口算，也就是把小数乘法转化成整数乘法来计算，最后再点小数点。这样口算出的答案对吗？你有哪些好方法来验证一下，请来详细解释一下吧。

生1：0.8元=8角，8角×3=24角，24角=2.4元。

生2：0.8+0.8+0.8=2.4。

生3：先把0.8×1 0=8，8×3=24，再把24÷10=2.4。

生4：0.8是8个十分之一，3个0.8就有24个十分之一，24个十分之一是2.4。

展示算理的动态过程：

师（小结）：同学们不仅凭着已有的知识和经验把小数乘法转化成整数乘法来计算，还能从不同的角度来解释这样算的理由是什么，很棒。

学生第一次面对小数乘法，首先需要理解这样的乘法是怎么来的，意义是什么。这个环节的教学侧重点是引导学生利用已有知识经验自主尝试探索出小数乘整数的口算方法。在教师适时的引导和启发下，学生呈现出四种口算的方法：第一种是基于现实背景下的思考，化元为角来计算;第二种是联系乘法的意义，利用小数加法来计算;第三种是依据积的变化规律来思考;第四种则是基于小数意义的认识类推出小数乘法的计算算理。在这里我们可以欣慰地看到学生能够自主地从不同角度多样化解决问题，在主动建构的过程中已经初步将新知纳入已有的认识系统之中，认知结构得到了进一步的完善。

三、立足经验，理出个性资源

出示例题图：学生自主尝试笔算2.35×3，展示笔算的思维过程：

师：仔细观察同学们算的过程，将它们理一理，哪些可以摆在一起？说说理由。

汇报：

（1）

生：这种是用加法算的。

师：用加法计算出的结果对吗？那2.35×3其实就是表示什么？

生：这两种不是列竖式算的。

师：先请这两位同学介绍一下自己的想法。同意他们的算法吗？你有没有看出他俩在计算过程中有相同点？

生1：都是先把2.35×3看成235×3来计算的。

生2：都是把小数乘法当成整数乘法来计算，最后再点上小数点。

生3：第一位同学是根据积的变化规律来点小数点，第二位同学是根据小数的意义来点小数点。

生：这四位同学都是列的乘法竖式。

师：先请这四位同学介绍自己是怎样计算的？听了他们的介绍，你有什么想说的？

生1：我不同意第一位同学的写法，3后面的小数点和两个零不需要寫出来。

生2：做加法的时候我们会这样写出来，乘法不需要，因为是算235×3的。

生3：我觉得最后一种写法也不对，3应该放在下方比较好，就像235×3时我们通常是把235摆放在上面，便于计算。

师：那对于中间两种的写法你们有什么想法呢？

（全场寂静，学生陷于沉思）

师：3跟个位的2对齐，我们在什么样的计算中是这样做的？

生4：2.35+3的时候。

师：那计算小数加法时为什么要3跟个位的2对齐？

生4：因为个位要跟个位相加。

生4：相同数位上的数才能相加减。

生5：我觉得乘法里面，3是要跟2.35的每个数位上的数相乘的，所以这里的3不需要跟个位的2对齐，就像235×3那样。

生5：因为我们是把2.35×3看成235×3来计算的，所以按照235×3的竖式那样对位就行了，同意第三种写法。

师：如果2.35×4113，你们还会把4113的3跟个位上的2对齐吗？

生：不会，竖式摆放太斜了，不好看。

师：那我们来总结一下，为什么小数乘整数竖式摆放时是末位对齐呢？

关于竖式摆放是数位对齐还是末位对齐，我们一般的做法是直接告知学生“可以这样列竖式计算”，似乎没有什么可以探究的问题，学生也是照模式套用下来。可事实上并非如此，学生并不明晰其中的道理，知其然而不知其所以然。小数乘法的竖式，为什么书上的写法是末位对齐，而不像小数加减法那样相同数位对齐呢？学生是存在不同的个性化问题的。真实呈现不同想法和思维过程，组织开展分类讨论研究，理清学生个性化方法里面存在的妥与不妥，个性化的自主建构也就逐步转变为达成共识的社会建构。

课堂教学是一个动态推进的过程。学生之间因为生存环境、思维方式方法和已有知识经验的不同，面对新问题会出现不同的个性化理解，形成一些个性化差异性资源。教学中真实地呈现这样的生成性材料，让学生大胆发表自己的见解，思一思、辩一辩，求同存异。生成性材料成为宝贵的教学资源，加上教师不失时机地点拨、追问，让看似平淡简单的环节变得有波澜、更深刻。在交流辨析中，小数乘法计算的算理和算法也就自然融合在一起。