基于ARIMA模型的酒店入住率预测分析
2020-10-15孙媛媛
基金项目:全国统计科学研究项目:大数据半参数混合效应模型的稳健统计分析及其应用研究,编号:2018LY40
摘 要:酒店入住率对酒店管理非常重要,其预先预测,可以有效减少管理不确定性,为酒店管理做出贡献,最大限度地利用利潤,但由于其多方面因素的影响,使酒店住宿数量预测复杂而且更难。本文首先根据数据特征分析和分析数据的特点,利用SAS软件建立处理后数据的时间序列模型,然后利用已知数据预测酒店未来的入住率,使复杂度的预测问题有一定的讨论。
关键词:酒店入住率;ARIMA模型;时间序列分析;预测
随着经济的快速发展和城市居民收入水平的不断提高,酒店业在城市中起着重要的作用,是城市旅游业的重要发展条件。自2001年以来,中国酒店数量在不断增加,行业竞争加剧。近年来,中国酒店市场不断壮大,各方预计会占领一份市场份额而努力[1]。近几年中国已经成为世界第三大旅游目的地,因而为抢占先机,国际酒店是首当其冲,全球最大的连锁酒店竞相进入中国。陈恩[2]认为我国旅游贸易进口增长情况要比出口情况好得多,这种顺差将为减轻总体服务贸易逆差有明显作用,从而对酒店服务业带来了可观的发展。针对以研究入境旅游、出境旅游与经济增长之间的关系为主的国内学者,对于出入境旅游快速发展的利弊,意见尚未统一。
赵进文[3](2006)利用Granger因果检验分析了区域经济在受到入境旅游的影响有哪些差异,研究显示出沿海东部地区所受到入境旅游的影响是相对比较突出的,但是就全国其他地区而言,入境旅游对当地经济发展的影响甚微,综上而言,入境旅游在全国还没有足够的发展。吴忠才[4](2007)则是通过构建协整模型,针对入境旅游与国内区域经济增长之间的模型关系进行分析,研究表明每当入境旅游增长1%,GDP则增长0.151%,但是,该结果显示,Granger因果关系模型并不适用于入境旅游以及GDP的关系模型。供求绝对平衡只是市场经济中一个理想的临时状态。经济学中的平衡点上下波动一直都是常态,酒店业也不例外。供需之间的平衡点的波动一直很大,导致酒店业所承担的风险性也很大。供应方面,由于政府的大力推动,酒店业已成为当今热门产业。因此,酒店行业迎来难得一遇的发展机遇。本文就对酒店入住率的时间序列分析为主题,收集相关数据,建立合适的数学模型,预测合理的酒店入住率,为酒店行业的管理者提高可行的参考建议。本文主要工作如下:(1)分析讨论盐城某酒店入住率变化趋势,建立适合盐城酒店入住率的最佳数量的模型,并进行预测。(2)预测酒店入住率数据,建立合理的模型,对当地政府提供可行的改善建议。
一、准备知识
(一)本课题的数学基础知识
《应用时间序列分析》和《经济预测与决策》阐述了时间序列分析中各种相关变量的推导过程,并且在模型拟合方面进行了基本介绍,使本论文的进行有了可参考的理论依据。
(二)时间序列分析
对于时间序列{Xt,t∈T},可以定义如下概率分布:
可以叫作序列{Xt}的概率分布族。
(三)非平稳时间序列
ARIMA(p,d,q)的模型结构如下:
式中,
(四)数据收集说明
笔者通过盐城市A酒店、B酒店两家五星级酒店客房部采访收集到了该两家酒店的12月份酒店入住率数据。
二、A酒店的入住率预测模型
(一)A酒店入住率数据的预处理
1.平稳性检验
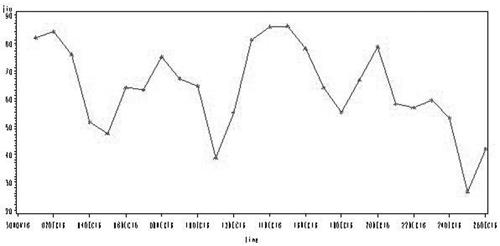
应用时间序列分析的核心是控制和预测。我们要对收集到的酒店入住率数据进行处理。我们提取出由于酒店入住率,随着时间的推移而发生改变,因此存在着时效性。这也体现了时间序列分析在处理数据过程中首要注重的问题,必须确保数据排除时效性的干扰,即保持平稳。为了分析数据的平稳性,我们借助统计软件SAS来完成。通过SAS对数据进行处理和分析,我们得到了盐城市某五星级酒店A酒店2019年12月1日至26日酒店入住率时序图(图2-1)。
图2-1 A酒店2019年12月1日至26日酒店入住率时序图
从图2-1可以看出,A酒店2019年12月1日至26日酒店入住率序列清晰地呈现出一定幅度的波动,由此可知A酒店2019年12月1日至26日酒店入住率序列不是平稳序列。为了进一步地判定其平稳性,我们对它的自相关图进行观察。
2.纯随机性检验
必须对A酒店入住率序列作纯随机检验,才能够判断其序列是否有分析价值。根据白噪声检验结果,在延迟12、18、24阶的x2检验统计量的P值小于0.05,说明序列是非白噪声序列,具有研究分析的价值,并对一阶差分后的A酒店入住率序列进一步拟合ARMA模型。
(二)模型建立
1.模型识别
差分运算与ARMA模型的组合实质上就是ARIMA模型。要使用ARMA模型对非平稳序列进行拟合,必须对其就行适当阶数的差分直至平稳。通常可以通过观察其自相关图和偏自相关图进行初步判断。一阶差分后序列的自相关图显示出显著的拖尾性,偏自相关图显示明显的非截尾性。
2.参数估计
根据运行结果对模型进行定阶。本文选择了一个可选命令minic,可以在一定范围内定阶。输出所有自相关延迟阶数和移动平均延迟阶数都小于等于8的ARMA(p,q)模型的BIC信息量,并指出其中BIC信息量最小时的模型的阶数,实现模型优化。运行结果显示,ARMA(3,2)为较优模型。我们用ARMA(3,2)模型进行拟合,并对其进行参数检验。参数估计输出结果不显著,考虑参数对模型的影响力,θ1-θ2、φ1-φ3中只有φ3一个参数的P值统计量是不显著的,重新对模型进行参数检验,而后当剔除φ3时,参数检验通过,确定ARMA(2,2)模型作为A酒店入住率序列的预测模型。确定好模型后则需要序列值。由ARMA(p,q)的理论基础可以知道,模型共包含p+q+1个未知参数。由于常数项已被剔除。那么我们需要估计出1阶差分后序列模型ARMA(2,2)的4个未知参数。我们选择较为常用的最小二乘估计。使残差平方和达到最小的对应参数值就是■的最小二乘估计值。且延迟各阶的P值均显著大于α(α=0.05),所以该拟合模型显著。我们得到模型ARIMA(2,1,2)为:
这就是我们根据盐城市某五星级酒店A酒店2019年12月1日至12月26日酒店入住率序列1阶差分后得到ARIMA(2,1,2)模型。
(三)模型预测
2019年12月1日至26日,该酒店的入住率最高为2009 年12月15日的。其中,2019年12月1日至26日共26天,入住率以上的有9天;2019年12月1日至26日共26天,平均入住率为。要预测酒店的运营情况,酒店入住率的预测至关重要。我们根据上文程序运行后所判断检验得到的1阶差分后的ARMA(2,2)模型,对12月1日至12月26日的某酒店入住率序列拟合的预测模型拟合后,本文利用ARIMA(2,1,2)模型对酒店入住率序列进行短期预测,该输出结果真实值均落入预测区间,ARIMA(2,1,2)模型预测效果良好,符合该酒店入住率的发展趋势。
三、B酒店的入住率预测模型
(一)B酒店入住率数据的预处理
1.平稳性检验
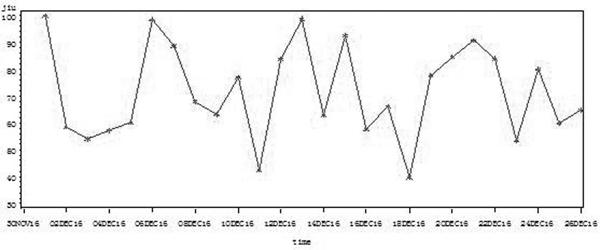
本文先对盐城市某五星级酒店B酒店2019年12月1日至26日酒店入住率数据做时序图(图3-1)。
从图3-1可以看出,B酒店2019年12月1日至26日酒店入住率序列呈现出上下不同幅度的波动,由此可知B酒店2019年12月1日至26日酒店入住率序列不是平稳序列。我们观察其自相关图。从而进一步判定其平稳性。
2.纯随机性检验
必须对B酒店入住率序列作纯随机检验,才能够判断其序列是否有分析价值。
根据SAS软件的运行结果,得到白噪声检验结果。检验结果说明,在延迟12、18、24阶的x2检验统计量的P值小于0.05,说明序列是非白噪声序列,具有研究分析的价值,并对一阶差分后的B酒店入住率序列进一步拟合ARMA模型。
(二)模型建立结果显示
1阶差分后序列的自相关图和偏自相关图显示初步判断p=1,q=5。B酒店2019年12月1日至26日酒店入住率1阶差分后序列初步拟合模型定阶为ARMA(1,5)。我们得到B酒店入住率序列1阶差分后ARMA(1,5)模型,并对该模型的参数进行参数检验。结果不显著,θ2、θ3、φ1的P值统计量小于α(α=0.05),不显著。考虑参数对模型的影响力,我们剔除θ2、θ3、φ1三个参数重新对模型进行参数检验,参数检验通过,确定B酒店2019年12月1日至26日酒店入住率序列1阶差分后模型定阶为MA((1),(4),(5))。由输出的残差自相关检验结果得,延遲各阶的P值均显著大于α(α=0.05),所以该拟合模型显著成立。
我们得到模型ARIMA(0,1,((1),(4),(5)))为:
(1-B)xt=(1-0.64739B-0.48954B4+0.42765B5)εt
这就是我们根据盐城市某五星级酒店2019年12月1日至12月26日酒店入住率序列得到ARIMA(0,1,((1),(4),(5)))模型。
(三)预测检验
我们根据上文程序运行后所判断检验得到的ARIMA(0,1,((1),(4),(5)))模型,对12月1日至12月26日的某酒店入住率序列拟合的预测。模型拟合后,本文利用ARIMA(0,1,((1),(4),(5))模型对酒店入住率序列进行短期预测,该输出结果显示真实值均落入预测区间,ARIMA(0,1,((1),(4),(5)))模型拟合的情况良好,预测曲线的变化趋势与真实值变动趋势相似,符合该酒店入住率的发展趋势。
四、两家酒店入住率的对比
本文研究盐城市某两家五星级酒店入住率,运用时间序列分析针对预测酒店入住率,通过实地调查,由于数据相关酒店内部运营,具有一定的保密性,所以笔者收集到12月份A酒店、B入住率序列数据,并对12月1日至12月26日之间的酒店入住率数据进行时间序列分析,建立ARIMA模型,并对模型进行检验,最后确定A、B酒店入住率序列对应模型为ARIMA(2,1,2)、ARIMA(0,1,((1),(4),(5))),并对A、B酒店两家酒店12月27日至31日数据进行预测,最终真实值落入预测区间,表明该模型符合该酒店入住率发展趋势。
A酒店入住率的模型为:
(1-1.20403B+0.87632B2)(1-B)xt=(1-1.49438B+0.9272B2)εt
B酒店入住率的模型为:
(1-B)xt=(1-0.64739B-0.48954B4+0.42765B5)εt
根据两家酒店的入住率序列所对应时序图以及预测区间,A酒店是当地老牌五星级酒店,拥有强厚的客户基础,但也正因为老牌五星级酒店,经营模式固化,对年轻群体的吸引力比较小,酒店入住率的增长受到限制。B酒店是当地新兴五星级商务酒店,主打年轻、商务等标签的群体,具有一定的商务特色,灵活多变的经营模式,也深受年轻群体的欢迎。
结束语:
研究结果表明:盐城酒店业还存在很大的发展空间。在未来的一段时间内,盐城市政府需大力加强对酒店行业的标准管理,与此同时,实时更新相关的旅游数据变化信息,促使当地酒店管理公司以及投资方及时掌握信息并制定出相应对的调整解决措施,避免供求不平衡所带来的不可控的市场冲击。通过建立区域性酒店业的咨询服务中心,对酒店业管理者和投资者给予专业指导和培训,正确引导酒店行业资金流,实现社会资金的最佳利用,促进了酒店行业的健康发展。
参考文献:
[1]国家外汇管理局.2006年中国国际收支报告[R].2007.
[2]陈恩,蔡丽.澳门旅游服务贸易国际竞争力及其影响因素的实证分析[J].西安财经学院学报,2006(01):106-108.
[3]赵进文,范继涛.经济增长与能源消费内在依从关系的实证研究[J].经济研究,2007(08):31-42.
[4]吴忠才.旅游竞争优势战略:旅游业发展的新战略观[J].经济问题探索,2007,22(07):106-108.
作者简介:孙媛媛(1995-),女,汉族,江苏省盐城市人,硕士,助教。研究方向:宏观经济、经济统计模型。
