环氧树脂封窜堵剂体系双阶段固化动力学分析*
2020-10-15黄雪莉
王 瑞,杨 彪,何 龙,黄雪莉
(1.河南油田石油工程技术研究院,河南郑州 473000;2.新疆大学化学化工学院,新疆乌鲁木齐 830000;3.中石化西北油田分公司石油工程技术研究院,新疆乌鲁木齐 830000)
环氧树脂是应用最广泛的热固性树脂之一,因其固化物具有良好的机械性能,以及耐磨、耐腐蚀性能和热稳定性能,被广泛用于涂料防腐、油田、电子产品以及复合建筑材料的各个领域[1-2]。环氧树脂本身是热塑性的,只有与固化剂配合使用,线性环氧树脂小分子在室温或加热状态下才能交联聚合,形成性能优异、具有利用价值的高分子材料[1,3]。环氧树脂固化物的性能主要取决于固化剂,不同种类的固化剂对应不同的反应机理,固化材料的性能和固化工艺也有所差异[4-5]。因此,对环氧树脂固化机理及固化动力学的研究可为树脂固化工艺及其应用提供理论依据和指导。
由于环氧树脂型堵剂封堵能力强,抗水稀释,固化后堵剂具有高强度、高韧性、耐腐蚀、低收缩和稳定周期长的特性,在油田封窜堵水方面受到广泛关注[6-7]。但是环氧树脂封窜堵剂组分复杂,固化过程与简单的环氧树脂与固化剂双组分不同,因此有关环氧树脂封窜堵剂的固化动力学研究对于封窜堵剂体系的应用指导就尤为重要。前期有众多学者对环氧树脂固化动力学进行了大量研究[8-12],但大部分针对树脂和固化剂的双组分体系。环氧树脂封窜堵剂中有稀释剂、促进剂及增韧剂等复杂成分,有关复杂组分环氧树脂固化体系动力学研究的报道较少。本文以三乙醇胺(TEOA)为固化剂,采用DSC 非等温测试法研究环氧树脂(E-51)/三乙醇胺封窜堵剂体系的固化动力学。根据DSC 曲线分析该固化体系的放热情况及固化机理,拟合出该体系的固化动力学方程参数。
1 实验部分
1.1 材料与仪器
环氧树脂(E-51),环氧当量为180数195 g/mol,无机氯值小于40 mg/kg,工业级,无锡市长干化工有限公司;三乙醇胺(TEOA)固化剂,胺值600数700 mg KOH/g,分析纯,无锡市长干化工有限公司;活性稀释剂(醚类)(有效含量≥99%),分析纯,天津中和盛泰化工有限公司。
NETZSCH DSC-3500 型差热扫描量热仪(DSC),德国耐驰公司。
1.2 非等温DSC测试
用活性稀释剂将环氧树脂(E-51)稀释至所需黏度,按比例加入固化剂TEOA,利用磁力搅拌器搅拌10数15 min,待树脂与固化剂混合均匀后得到树脂浆液,此配制过程均在室温下进行,且必须现配现用。取8数10 mg 树脂浆液于铝制坩埚中,将坩埚放入差热扫描量热仪待测样品池中,采用非等温法,分别以5、10、15、20 K/min 的升温速率,从室温开始升温至200℃(473.15 K),用高纯氮气保护(50 mL/min),测定环氧树脂非等温固化过程中的放热曲线。
2 结果与讨论
2.1 环氧树脂封窜堵剂固化体系非等温DSC 测试分析
环氧树脂封窜堵剂固化体系的非等温DSC 测试曲线如图1所示。在5、10、15、20 K/min的升温速率下,环氧树脂体系的固化热流速率曲线有两个明显的放热峰,充分说明该体系的固化过程是一个复杂的过程,且环氧树脂封窜堵剂固化体系的固化过程分为两个阶段[13]:第一阶段对应DSC放热曲线的第一个峰,为环氧树脂的环氧基团与固化剂TEOA的羟基发生亲核加成反应,树脂达到初步凝胶化。从放热峰面积来看,随着升温速率的逐渐升高,初步凝胶化程度也逐渐增加,且峰顶对应的特征温度值也随之增加。第二阶段对应DSC 放热曲线的第二个峰,为分子内部的自缩聚反应,在叔胺基团的促进作用下,分子内部的羟基进一步发生缩聚反应。第二阶段反应中随着升温速率的增加,峰顶对应的特征温度值也逐渐增加,但是总放热量随之减少。这是由于对于特定环氧树脂堵剂配比体系,从初始反应到完全固化,整个过程中反应的放热焓是一定的,当第一阶段即凝胶化阶段放热量增加时,第二阶段固化阶段的放热量就会减少。将非等温DSC 曲线的特征值汇总在表1 中。由表可见,不同升温速率下的总放热焓值稍有变化,在较低升温速率下,反应的总放热焓较大,随着升温速率的增高,放热焓有所减少。造成这种现象的原因可能有两方面[14]。一是由于升温速率过快,DSC测量过程中温度补偿的滞后效应造成;二是因为升温速率加快时,环氧树脂与固化剂的反应更加迅速,环氧树脂小分子向体型结构增长的时间缩短,相同时间内反应程度比低升温速率时更充分,从而导致后续自缩聚阶段受阻,放热量也相对减少。
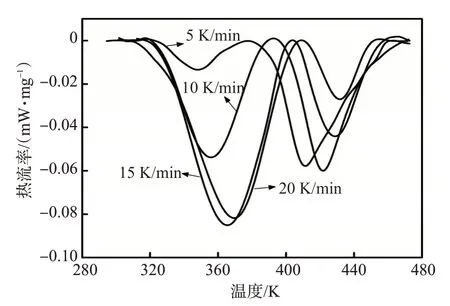
图1 环氧树脂封窜堵剂固化体系DSC测试曲线
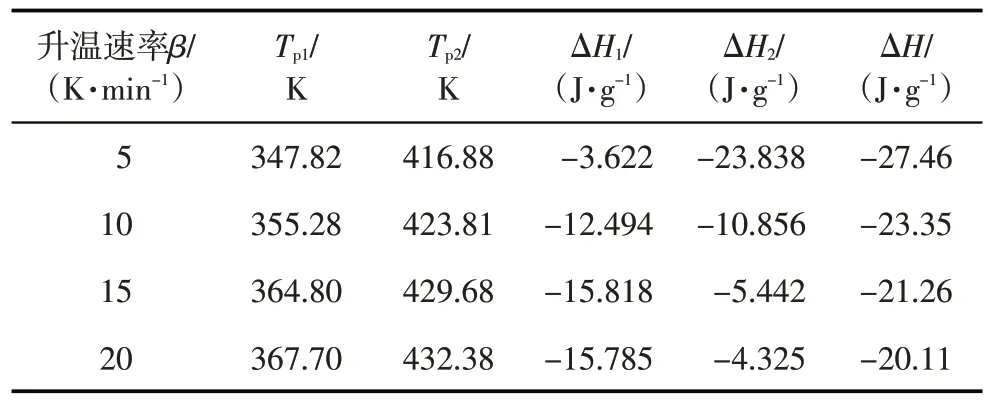
表1 不同升温速率下环氧树脂封窜堵剂固化体系DSC峰值温度和放热焓
为方便分析动力学过程,采用分峰法将环氧树脂封窜堵剂固化DSC 曲线进行分峰处理[10,14],结果如图2、图3所示。
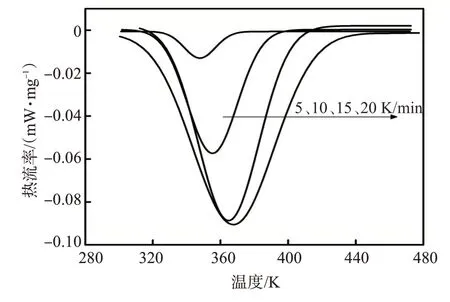
图2 环氧树脂封窜堵剂体系凝胶峰(峰1)
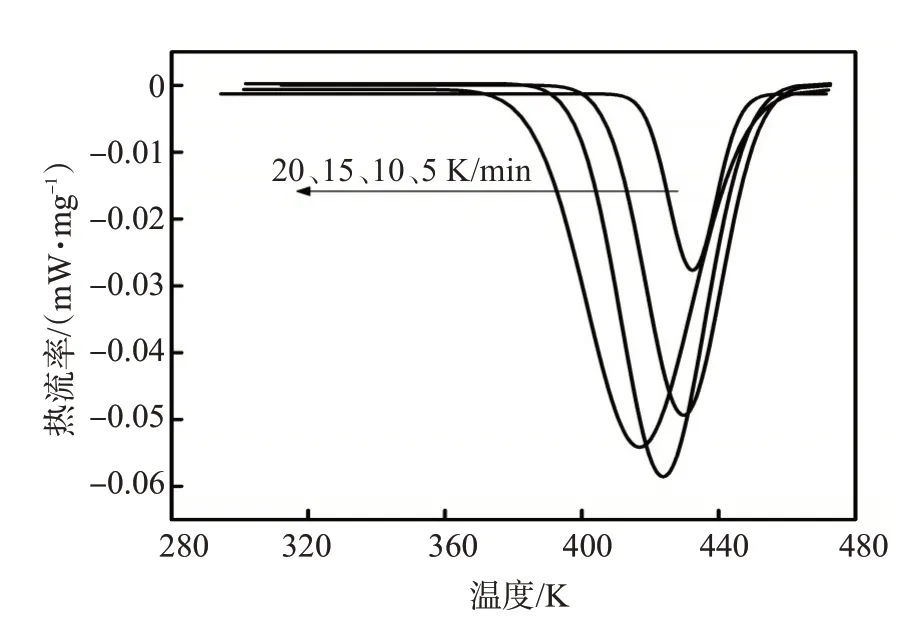
图3 环氧树脂封窜堵剂体系固化峰(峰2)
2.2 环氧树脂封窜堵剂固化机理函数模型
采用差热扫描量热(DSC)法研究环氧树脂固化动力学,主要基于2个基本假设[15],即:(1)假设固化反应速率与热流率成正比关系;(2)假设固化反应放热焓变与固化度成正比关系(即反应放热曲线面积正比反应放热焓),可用式(1)和式(2)表示。
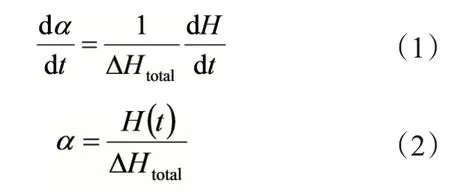
式中,dα/dt—固化反应速率;△Htotal—总反应放热焓,J/g;dH/dt—热流率,mW/mg;H(t)—t 时刻的放热焓,J/g;α—固化程度。而固化反应速率基本方程为:
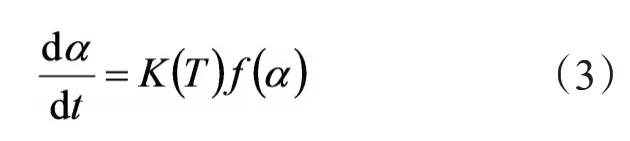
其中,K(T)—反应速率常数,遵循Arrhenius方程(式4):
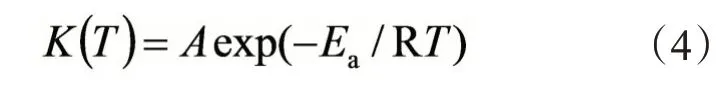
式中,R—气体常数,8.314 J/(mol·K);Ea—固化反应活化能,J/mol;A—指前因子;T—温度,K。
f(α)为固化度α的固化机理函数,形式与固化机理有关。由式(2)对峰1数据进行计算,并拟合作图得到环氧树脂封窜堵剂凝胶阶段温度与固化度的关系曲线,如图4所示。由图4峰1温度与固化度的关系曲线可以看出,反应刚开始阶段,固化度为0;随温度逐渐增加,固化度迅速增加并达到峰值;峰值之后反应速率下降,固化度趋于稳定。固化度曲线是完整的S型自催化曲线,因此,固化机理函数选择Sestak 与Berggrem 提出的双参数(m,n)自催化模型(Sestak-Berggrem 模型,简称SB 模型)[11]。固化反应速率模型方程为:

式中,m、n—反应级数。
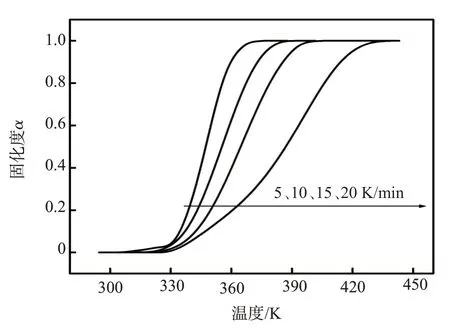
图4 环氧树脂封窜堵剂凝胶峰(峰1)温度与固化度α的关系曲线
2.3 封窜堵剂固化反应活化能Ea的计算
以Kissinger 方程[16]对不同升温速率和对应的峰顶温度进行线性拟合,计算得到固化反应的活化能Ea。Kissinger方程经变形后为:
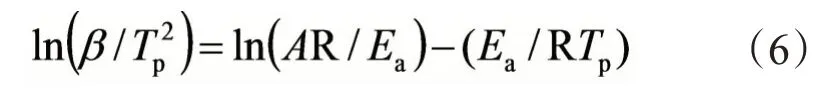
其中,β—升温速率,K/min;Tp—峰顶温度,K。
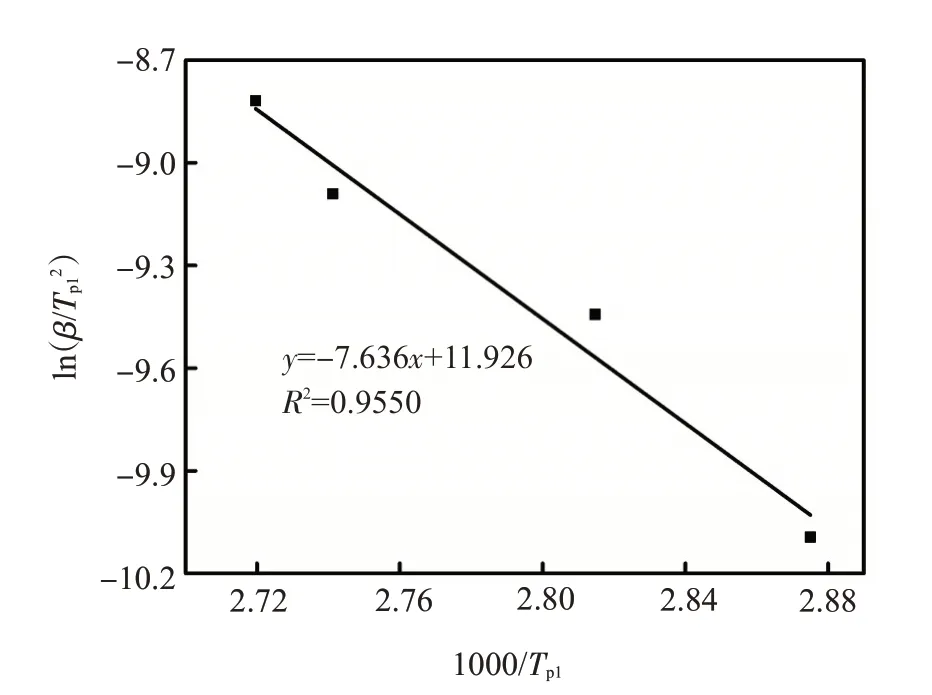
图5 峰1 ln(β/Tp12)与1000/Tp1的线性关系
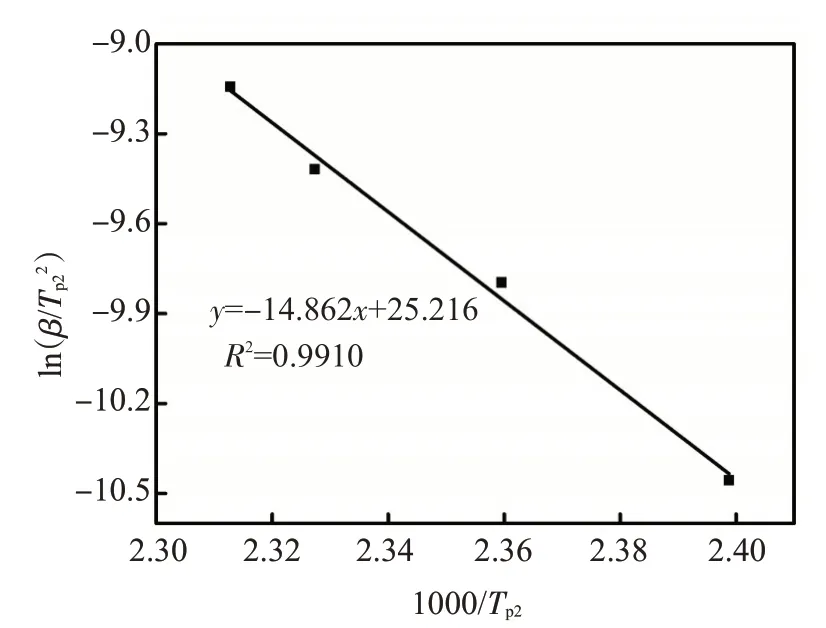
图6 峰2 ln(β/Tp22)与1000/Tp2的线性关系
2.4 反应级数m、n的确定
为了确定反应级数m和n的值,Malek等[17]引入了两个特殊形状因子函数y(α)与z(α),见式(7)和式(8)。
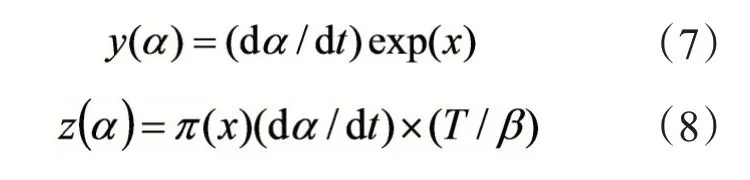
式中,x=(Ea/RT),Ea由kissinger方程确定,π(x)为温度的积分形式,表达式可以用Senum等[18]提出的方程近似表达(式9),即为:
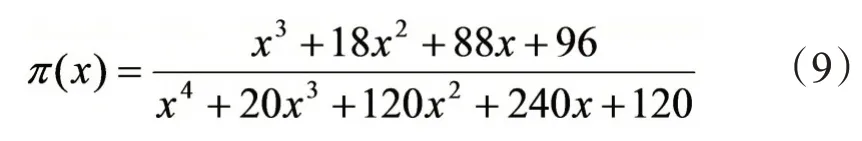
根据Malek 所提出的方程,拟合固化度和y(α)与z(α)的关系曲线,得到y(α)与z(α)曲线最大值所对应的固化度分别为αM和αp∞。峰1与峰2所对应的αM和αp∞值见表2,其中P=αM/(1-αM)=m/n。由Malek提出的判据,当0<αM<αp∞、且αp∞≠0.632 时,则认为环氧树脂固化反应符合自催化(m,n)模型。
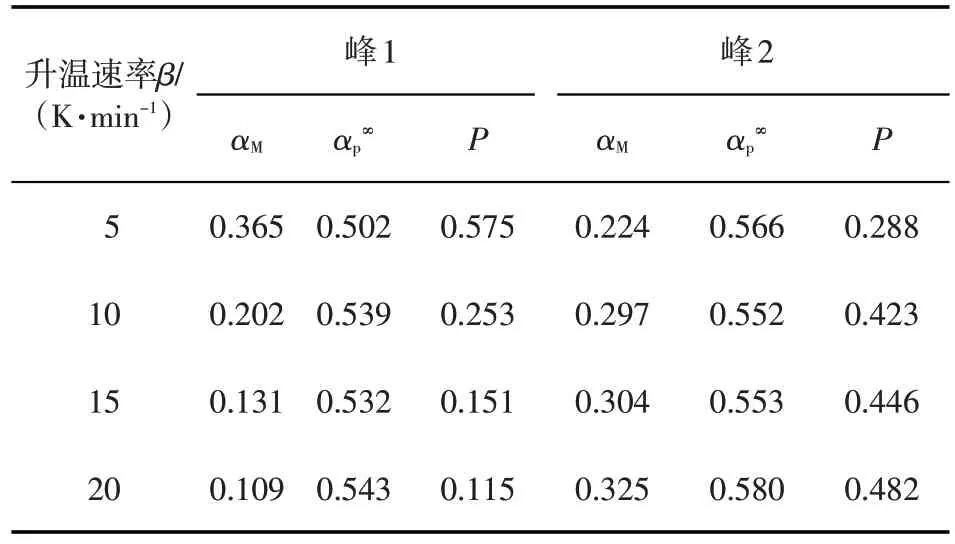
表2 峰1、峰2 y(α)与z(α)曲线的峰值αM、αp∞及相关参数
将固化反应动力学模型方程(式(5))两边取对数变形得:

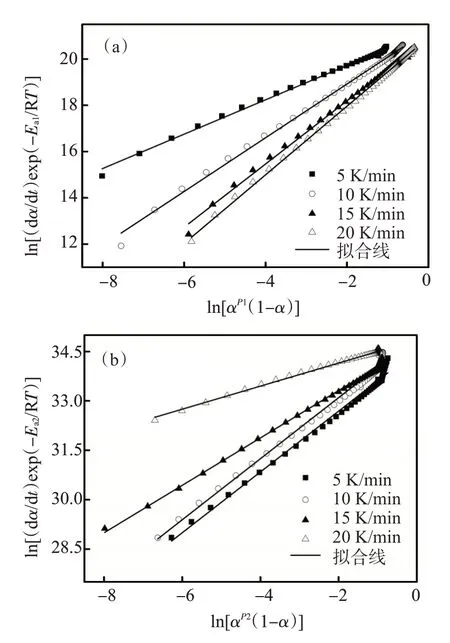
图7 峰1(a)和峰2(b)ln[(dα/dt)exp(-Ea/RT)]与ln[αP(1-α)]线性拟合图
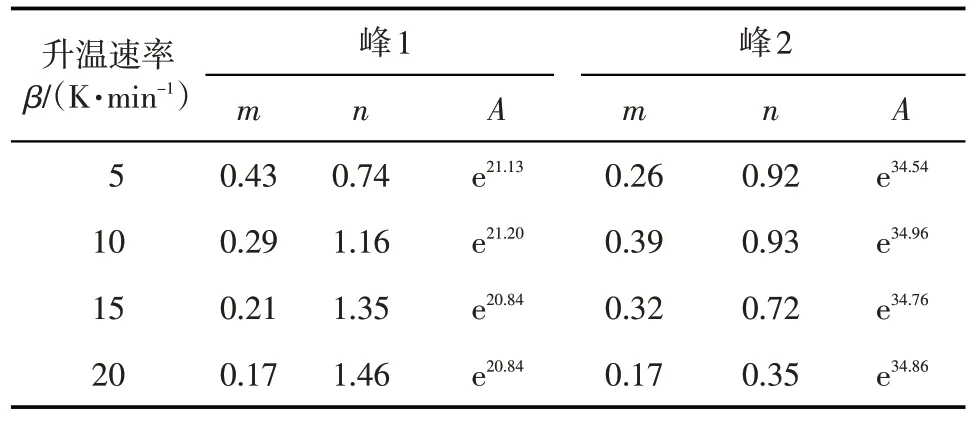
表3 不同升温速率下自催化模型动力学参数
2.5 动力学模型与实验数据拟合
将所得参数代入双参数自催化模型方程式(5),得到动力学方程,并将所得动力学方程拟合曲线与实际固化反应的实验曲线进行对比,如图8 所示。由图8 可见,(m,n)自催化动力学模型能很好的体现环氧树脂封窜堵剂的固化速率,并且有较高的吻合程度。
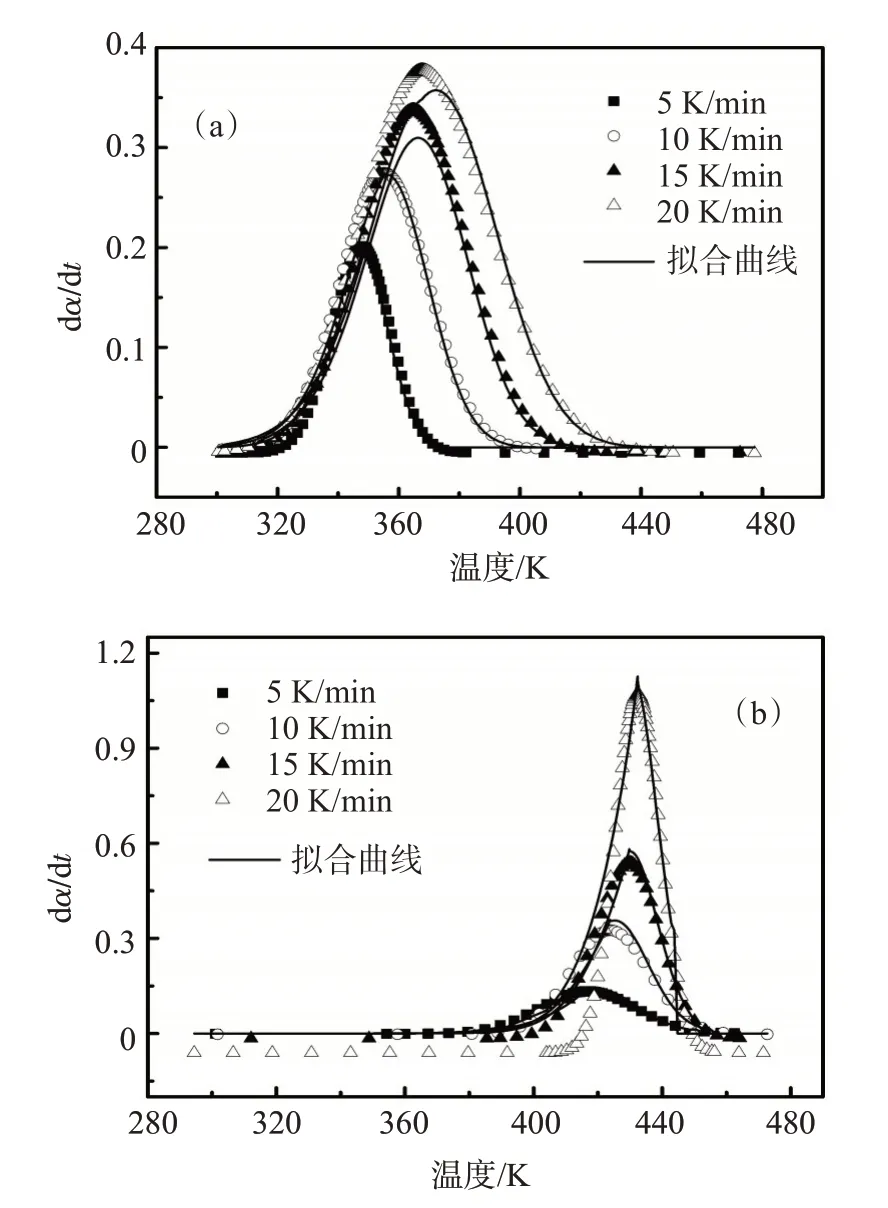
图8 峰1(a)、峰2(b)自催化模型与实验数据对比图
3 结论
以三乙醇胺(TEOA)为固化剂,采用DSC 非等温测试法研究双酚A 型环氧树脂的固化动力学。环氧树脂封窜堵剂固化过程过程中有两个明显的放热峰,其固化反应机理为双阶段固化过程。第一阶段为凝胶化阶段,也为催化阶段;第二阶段为固化阶段。
采用Kissinger 方程拟合出凝胶化阶段与固化阶段的固化反应活化能分别为Ea1=63.489 kJ/mol,Ea2=123.560 kJ/mol。固化阶段的活化能约为凝胶化阶段活化能的2 倍。由于反应位阻效应的影响,固化阶段的反应活性远低于凝胶阶段。
采用双参数(m,n)自催化模型拟合得到该堵剂体系的固化动力学方程与实验数据的吻合度良好,能较好地表示该固化体系的反应速率。
致谢:本文在写作过程中得到西北油田分公司刘耀宇、河南油田李洲的许多帮助,在此表示感谢!
