开槽变截面人行桥的气动性能与TMD减振研究
2020-10-15赵军杰牛华伟陈政清周子祺郑甲强黄文理
赵军杰,牛华伟,陈政清,周子祺,郑甲强,黄文理
开槽变截面人行桥的气动性能与TMD减振研究
赵军杰1, 2,牛华伟1,陈政清1,周子祺3,郑甲强4,黄文理5
(1. 湖南大学 风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082;2. 中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;3. 佛山市铁路投资建设集团有限公司,广东 佛山 528000;4. 德化县上涌镇村镇规划建设环保站,福建 泉州 362500;5. 德化县美湖镇村镇规划建设环保站,福建 泉州 362500)
针对开槽变截面这一新型桥梁断面,为研究其颤振与涡振性能,以某人行桥为工程背景,制作缩尺比为1/29的全桥气弹模型进行风洞试验。设计电涡流杠杆式和悬臂式TMD,研究其减振效率。研究表明:在0°和±3°风攻角和0°,15°,30°,45°,60°和90°风偏角下,主梁颤振临界风速均大于颤振检验风速(104.4 m/s);设计基准风速范围(0~58.4 m/s)内,在0°和±3°风攻角及0°,15°和30°风偏角下,主梁发生1阶竖弯、1阶扭转及2阶竖弯涡振;与0°风攻角相比,在+3°风攻角下,1阶与2阶竖弯涡振风速锁定区间有延迟,振幅分别减小和增大;布置TMD之后,涡振风速锁定区间几乎不变,振幅最大值对应的风速减小,振幅分别减少46%,47%和77%。
开槽变截面;人行桥;颤振;涡振;电涡流TMD
人行玻璃桥和观景平台景观效果好,可以满足游客的审美需求,越来越多地出现在景区建设中,但该类结构往往柔性大、质量轻,风振响应明显[1−4]。与一般玻璃桥相比,本文研究的玻璃景观平台造型奇特,风振响应特性复杂,不但缺乏合理的规范设计条文,而且缺少可直接参考的研究文献,必须通过风洞试验进行专门研究。国内外的大跨度桥梁设计中,中央开槽断面因其颤振性能优越而被广泛采用,如西堠门大桥、香港昂船洲大桥和墨西拿海峡大桥等方案。在实际工程和试验研究中,开槽断面常伴随严重的涡激共振现象[5−6]。它在低风速下发生,虽不会振动发散导致结构破坏,但是会影响到人体舒适度,使结构发生疲劳破坏。在现有桥梁断面风振特性研究中,一般基于二维条带假定使用比例1/80~1/40的节段模型进行测试,但变截面梁常常需要通过三维气弹模型来进行风振响应测试[7−8]。调谐质量阻尼器(Tuned Mass Damper,TMD)是一种构造简单、实用可靠的被动耗能减振装置。该装置已经在工程结构减振控制中广泛应用,如高耸结构振动控制[9−10]、大跨桥梁风致振动控制[11−12],大跨人行桥或楼板人致振动减振[13−15]。以上研究的桥梁断面均为等截面,槽宽比未达到0.3以上且未基于大比例全桥气弹模型研究电涡流悬臂式和杠杆式调谐质量阻尼器(LTTMD)的振动控制方案。本文以某观景平台为工程背景,制作了缩尺比为1/29的大比例全桥气弹模型,研究其风振响应及TMD减振性能,相关试验方法和成果可为同类结构物的气动性能及减振研究提供有价值的参考。
1 工程背景及有限元分析
某观景平台为单悬臂斜塔斜拉结构。倾斜主塔采用钢筋混凝土结构,通过桩基础和锚杆与山体坡面固结。拉索从主塔侧面与主纵梁相连接,梁上标准索距5.2 m,如图1。主梁单悬臂长度为60 m,采用开槽变截面悬挑断面,如图2。玻璃板铺设于主纵梁、次纵梁、小纵梁及挑横梁组成的框架之上直接承受人群荷载。主纵梁之间由横梁连接以增加主梁的抗扭刚度,如图3。由于该平台位于某沿海省份,常年经受台风、季风影响,工程建设采用的桥面高度处设计基准风速为58.4 m/s。

单位:cm

单位:mm
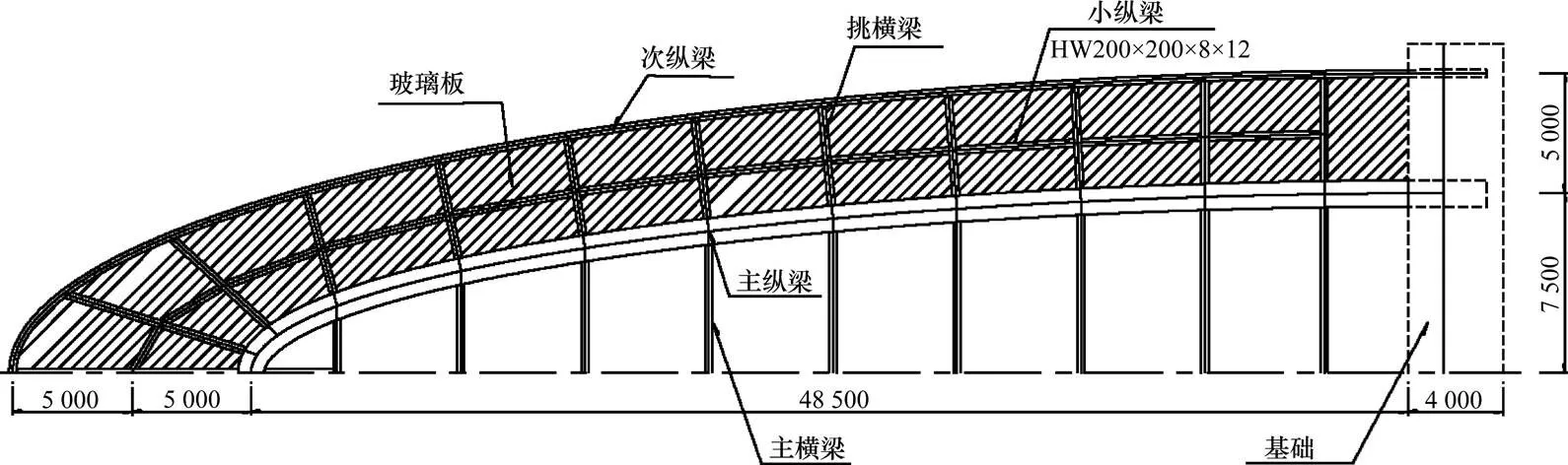
单位:mm
采用大型通用有限元软件ANSYS建立全桥模型,分析桥梁的动力特性。建模时,索塔及主梁各构件采用Beam188梁单元,玻璃桥面板及栏杆等附属设施采用Mass21质量单元。拉索采用Link8单元,索护套的质量通过调整拉索材料密度均匀施加。拉索两端分别与主纵梁及索塔共用节点,主梁根部与索塔根部共用节点。由于索塔锚固于山坡上,建模时约束其各节点全部自由度。桥梁自振频率与振型见表1。

表1 桥梁的自振频率与振型
2 风洞试验
2.1 气弹模型设计与动力特性检验
考虑到观景平台的实际尺寸、风洞试验段的尺寸以及模型可采购的标准型材尺寸,设计选取几何缩尺比为1/29,风速比和频率比分别为1/5.385和5.385/1。
主纵梁采用钢芯梁提供刚度,外衣采用3D打印工艺制作而成,次纵梁、小纵梁、横梁、玻璃板和内外侧栏杆等构件均由ABS板经数控雕刻机制作而成。固定在山坡上的主塔采用等效刚度处理,在塔根处向上沿着竖向设置实心的矩形钢棒模拟刚性桥塔。拉索的刚度根据线刚度等效原则进行模拟,其刚度与分布质量分别通过弹簧和集中质量块来模拟。气弹模型通过刚性支架固定于转盘上,以确保风向角和风攻角根据试验需要可调。气弹模型主梁长2.069 m,宽0~0.872 m,高0.038 m,如图4。经测试,气弹模型模拟的主要模态动力特性见表2,其中固定和放松TMD的试验工况在4.2.1节有详细说明。
2.2 风洞试验设计
采用上述气弹模型检验观景平台主梁的颤振稳定性,在湖南大学HD-2风洞高速试验段进行试验。来流风速在0~58 m/s之内连续可调。实际主梁的设计基准风速和颤振检验风速分别为58.4 m/s和104.4 m/s,采用风速比为1/5.385,对应模型的测试风速为10.8 m/s和19.4 m/s,因此试验测试风速控制在0~19.5 m/s范围内。试验时,在主梁端部与跨中两侧分别布置非接触式激光位移计,观测主梁的竖向与扭转振动响应。

图4 气弹模型风洞试验
3 气动性能分析
3.1 颤振稳定性
风洞试验考虑了风向角与风攻角的影响,测试工况和模型颤振临界风速测试结果见表3。可见,观景平台在颤振检验风速范围内未发现发散振动,其颤振稳定性满足设计要求。

表3 模型颤振临界风速
3.2 涡振特性
为了研究观景平台的涡激振动特性,根据设计关心的问题和结构特点,考虑来流风向的随机性及三维绕流现象,分别测试了不同风攻角和风向角下的风振响应。各工况下主梁端部竖向位移、跨中扭转角及竖向位移幅值的测试结果见图5~7,其中位移幅值和风速均为模型值。图例中“0°风偏角+3”代表0°风偏角+3°风攻角工况,“0°风偏角”代表0°风偏角0°风攻角工况。
在0°风偏角下,当风速在1.13,2.84和 4.48 m/s附近时,主梁端部竖向位移、跨中扭转角及竖向位移幅值依次发生了明显突变。当其发生突变时,主梁位移时程曲线较为正弦,因此可判定发生的振动不是抖振。结合频谱分析结果发现模型振动的卓越频率依次为1.953,4.981和6.504 Hz,接近模型的1阶竖弯、1阶扭转及2阶竖弯模态基频,因此可以断定主梁依次发生了1阶竖弯、1阶扭转和2阶竖弯涡激共振。
1阶竖弯涡振幅值最大值发生在0°风偏角0°风攻角下,此时端部竖向位移为2.31 mm,如图5所示。在0°风攻角下改变风偏角,发现在0°,15°和30°风偏角下也存在涡激共振现象,振幅依次减小。在45°,60°和90°风偏角下没有出现1阶竖弯涡激共振。在0°风偏角下改变风攻角,发现在0°,−3°和+3°攻角下发生了涡激共振,振幅依次减小,且当攻角为+3°时,涡激共振风速锁定区间有明显 延迟。

图5 端部竖向位移幅值

图6 跨中扭转角幅值

图7 跨中竖向位移幅值
1阶扭转涡振幅值最大值发生在15°风偏角0°风攻角下,此时跨中扭转角为0.19°,如图6所示。在0°风攻角下改变风偏角,发现在15°,0°和30°风偏角下发生了涡激共振,振幅依次减小。在45°,60°和90°风偏角下没有出现1阶扭转涡激共振。在0°风偏角下改变风攻角,发现在+3°,0°和−3°攻角下发生了涡激共振,振幅依次减小。
2阶竖弯涡振幅值最大值发生在0°风偏角+3°风攻角下,此时跨中竖向位移为1.31 mm,如图7所示。在0°风攻角下改变风偏角,发现在0°,15°和30°风偏角下存在涡激共振现象,振幅依次减小。在45°,60°和90°风偏角下没有出现2阶竖弯涡激共振。在0°风偏角下改变风攻角,发现在+3°,0°和−3°攻角下发生了涡激共振,振幅依次减小,且当攻角为+3°时,涡激共振风速锁定区间有明显 延迟。
4 电涡流TMD减振性能研究
4.1 阻尼器设计
在观景平台结构设计中,应人致振动舒适度的要求设置了减振TMD,提高了结构竖向与扭转模态的阻尼比,在减小人致振动的同时也会对风振有抑制作用。为了评估该TMD方案对风振特性的影响,本文研究中也根据模型频率设计了电涡流TMD,以改变气弹模型的等效阻尼特性。
根据人致振动TMD设置方案,电涡流TMD的最优频率和最优阻尼比为:

式中:opt=d/s为TMD与模型频率的比值,=d/为TMD与模型质量的比值,opt为TMD的最优阻尼比。对应1阶竖弯、1阶扭转和2阶竖弯模态的TMD参数如表4,其中各符号的含义与上式中的相同。实际设计中取质量比为0.015,TMD质量单元由磁钢和质量块总质量构成,刚度单元采用弹性钢片或弹簧,阻尼单元采用电涡流阻尼。由于1阶竖弯频率只有1.825 Hz,弹簧净伸长过长,一般的弹簧和弹簧片无法满足安装使用要求。本研究采用杠杆原理,杠杆比例取3,将弹簧刚度放大9倍,克服了该问题。固定和放松TMD时模型的动力特性见表2。

表 4 阻尼器设计参数
4.2 减振性能试验
4.2.1 试验设计
减振试验在开始前重新粘贴了气弹模型的内外侧栏杆,导致阻尼比变大。为了重点研究电涡流阻尼器的减振性能,分别测试了固定和放松阻尼器时模型的阻尼比,见表2。布置TMD前后,1阶竖弯、1阶扭转及2阶竖弯模态阻尼比分别由0.88%,1.48%,2.11%增大至2.95%,3.41%,5.35%。TMD布置情况如图4,图中V1,T1及V2分别代表控制1阶竖弯、1阶扭转及2阶竖弯的TMD。针对0°风攻角、0°风偏角工况,测试TMD的减振性能。
4.2.2 减振效果分析
布置TMD前后,主梁端部竖向位移、跨中扭转角及跨中竖向位移幅值测试结果见图8~10,其中位移和风速均为模型值。发生1阶竖弯、1阶扭转及2阶竖弯涡激共振时,放松TMD后,主梁端部竖向位移、跨中扭转角及跨中竖向位移幅值分别由1.16 mm,0.068°,0.84 mm降到了0.63 mm,0.036°,0.19 mm,减振效率依次为46%,47%和77%。观察涡激共振的风速锁定区间可见,阻尼比增大后,涡振风速锁定区间几乎不变,振幅最大值对应的风速减小。

图8 端部竖向位移幅值
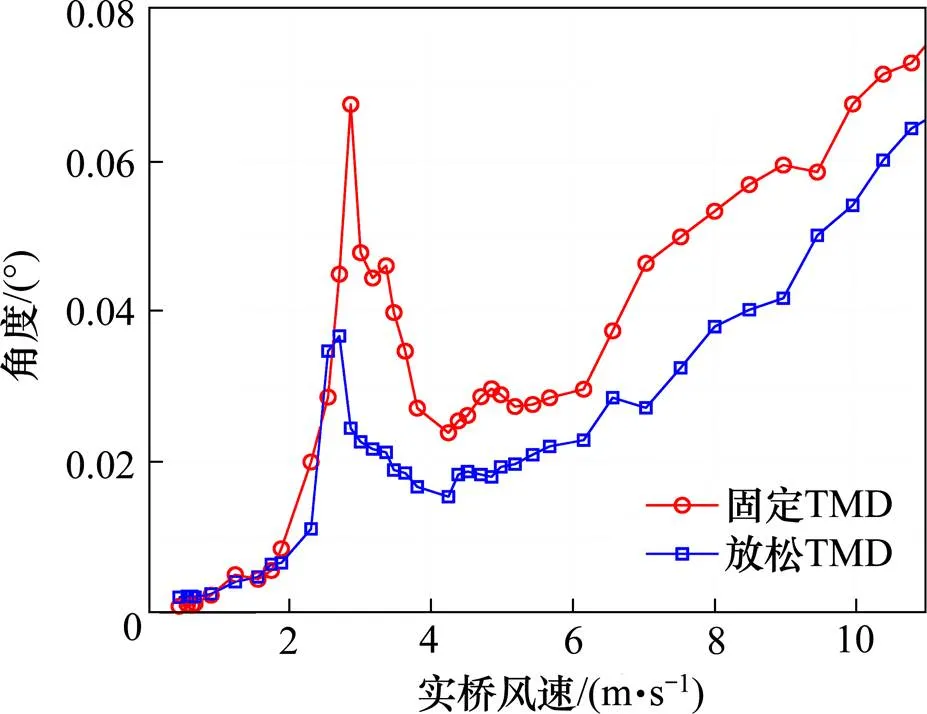
图9 跨中扭转角幅值

图10 跨中竖向位移幅值
5 结论
1) 在0°,+3°,−3°风攻角和0°,15°,30°,45°,60°,90°风偏角下,主梁颤振临界风速均大于颤振检验风速(104.4 m/s),颤振稳定性有足够的保证。
2) 设计基准风速范围(0~58.4 m/s)内,在0°,+3°,−3°风攻角和0°,15°,30°风偏角下,主梁依次发生明显的1阶竖弯、1阶扭转及2阶竖弯涡激共振,涡振性能极差。与0°风攻角相比,+3°风攻角下,1阶与2阶竖弯涡振风速锁定区间有明显延迟,振幅分别减小和增大。
3) 在0°风攻角、0°风偏角下,布置电涡流悬臂式和杠杆式TMD之后,主梁的1阶竖弯、1阶扭转及2阶竖弯模态等效阻尼比分别由0.88%,1.48%,2.11%增大至2.95%,3.41%,5.35%。随着阻尼比的增大,涡振风速锁定区间几乎不变,振幅最大值分别减少46%,47%和77%,振幅最大值对应的风速减小。
[1] 白桦, 李德锋, 李宇, 等. 人行悬索桥抗风性能改善措施研究[J]. 公路, 2012(12): 1−6. BAI Hua, LI Defeng, LI Yu, et al. Study on measures to improve wind resistance performance of pedestrian suspension bridge[J]. Highway, 2012(12): 1−6.
[2] 何恺, 郭坤, 马亮. 提高大跨度人行悬索桥抗风稳定性措施的效果分析[J]. 世界桥梁, 2017, 45(3): 69−74. HE Kai, GUO Kun, MA Liang. Effects of measures to improve wind resistance of long span pedestrian suspension bridge[J]. World Bridge, 2017, 45(3): 69−74.
[3] 易绍平, 徐晖, 吴明远, 等. 天蒙人行悬索桥抗风性能风洞试验研究[J]. 公路, 2016, 61(7): 173−176. YI Shaoping, XU Hui, WU Mingyuan, et al. Wind tunnel test on wind resistance of Tianmeng pedestrian suspension bridge[J]. Highway, 2016, 61(7): 173−176.
[4] 陈以荣, 曹张, 刘志文, 等. 钢桁架人行桥行人风环境及抗风性能研究[J]. 振动与冲击, 2019, 38(16): 274− 280. CHEN Yirong, CAO Zhang, LIU Zhiwen, et al. A study on pedestrian level wind environment and wind resistance performances of a steel truss foot-bridge[J]. Journal of Vibration and Shock, 2019, 38(16): 274−280.
[5] 艾国柱, 夏华晞. 悬索桥的加劲桁架—明石海峡大桥加劲桁架和加劲箱梁的比选[J]. 国外桥梁, 2000(4): 15−20. AI Guozhu, XIA Huaxi. Selection of stiffened truss and stiffened box girder of Mingshi strait bridge for suspension bridge[J]. Overseas Bridges, 2000(4): 15−20.
[6] 张伟, 魏志刚, 杨詠昕, 等. 基于高低雷诺数试验的分离双箱涡振性能对比[J]. 同济大学学报, 2008, 36(1): 6−11. ZHANG Wei, WEI Zhigang, YANG Yongxin, et al. Comparison and analysis of vortex induced vibration for twin-box bridge section based on experiments in different Reynolds numbers[J]. Journal of Tongji University, 2008, 36(1): 6−11.
[7] 苏益, 李明水, 杨阳, 等. 山区单悬臂廊桥结构抖振响应及等效风荷载[J]. 西南交通大学学报, 2019, 54(1): 121−128. SU Yi, LI Mingshui, YANG Yang, et al. Buffeting response and equivalent wind load of single cantilever corridor bridge in mountainous areas[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 121−128.
[8] 桂龙辉, 谢霁明, 林颖孜, 等. 悬挑环形廊桥的气动弹性模型试验[J]. 浙江大学学报(工学版), 2017, 51(11): 2121−2129. GUI Longhui, XIE Jiming, LIN Yingzi, et al. Aeroelastic model study of cantilever skywalk bridge[J]. Journal of Zhejiang University (Engineering Edition), 2017, 51(11): 2121−2129.
[9] 闫维明, 纪金豹, 蒋华戈, 等. 新型悬吊式TMD及其在某标志塔风振控制中的应用[J]. 建筑结构学报, 2010, 31(2): 55−60. YAN Weiming, JI Jinbao, JIANG Huage, et al. A new type pendlous TMD and its application on a tower for wind-induced vibration[J]. Journal of Building Structures, 2010, 31(2): 55−60.
[10] LU X, ZHANG Q, WENG D, et al. Improving performance of a super tall building using a new eddy current tuned mass damper[J]. Structural Control and Health Monitoring, 2017, 24: e1882.
[11] 雷旭, 牛华伟, 陈政清, 等. 大跨度钢拱桥吊杆减振的新型电涡流TMD开发与应用[J]. 中国公路学报, 2015,28(4): 60−68, 85. LEI Xu, NIU Huawei, CHEN Zhengqing, et al. Development and application of a new type eddy current TMD for vibration control of hangers of longspan steel arch bridges[J]. China Journal of Highway and Transport, 2015,28(4): 60−68, 85.
[12] 王志诚, 许春荣, 吴宏波. 崇启大桥主桥钢箱梁TMD系统设计参数计算研究[J]. 土木工程学报, 2015, 48(5): 76−82. WANG Zhicheng, XU Chunrong, WU Hongbo. Study on design parameters of TMD system for steel box girder of Chongqi Bridge[J]. China Civil Engineering Journal, 2015, 48(5): 76−82.
[13] 吕西林, 丁鲲, 施卫星, 等. 上海世博文化中心TMD减轻人致振动分析与实测研究[J]. 振动与冲击, 2012, 31(2): 32−37, 150. LÜ Xilin, DING Kun, SHI Weixing, et al. Analysis and field test for human-induced vibration reduction with TMD in Shanghai EXPO culture center[J]. Journal of Vibration and Shock, 2012, 31(2): 32−37, 150.
[14] 华旭刚, 温青, 陈政清, 等. 大跨度双层曲线斜拉桥人致振动减振优化与实测验证[J]. 振动工程学报, 2016, 29(5): 822−830. HUA Xugang, WEN Qing, CHEN Zhengqing, et al. Design and experimental validation of structural vibration control of a curved twin-deck cable-stayed bridge subject to pedestrians[J]. Journal of Vibration Engineering, 2016, 29(5): 822−830.
[15] Caetano E, Álvaro Cunha, Moutinho C, et al. Studies for controlling human-induced vibration of the PedroeInês footbridge, Portugal. Part 2: Implementation of tuned mass dampers[J]. Engineering Structures, 2010, 32(4): 1082−1091.
Study on aerodynamic performance and TMD vibration damping of foot bridge with slotted variable cross-section
ZHAO Junjie1, 2, NIU Huawei1, CHEN Zhengqing1, ZHOU Ziqi3, ZHENG Jiaqiang4, HUANG Wenli5
(1. Key Laboratory for Wind and Bridge Engineering of Hunan Province, Changsha 410082, China;2. Power China Zhongnan Engineering Corporation Limited, Changsha 410014, China;3. Foshan Railway Investment Construction Group Co., Ltd., Foshan 528000, China;4. Station for Planning, Construction and Environmental Protection in Shangyong Town, Quanzhou 362500, China;5. Station for Planning, Construction and Environmental Protection in Meihu Town, Quanzhou 362500, China)
In order to study the flutter and vortex-induced vibration performance of bridge with the slotted variable cross-section, the whole-bridge aeroelastic model of a foot bridge was made for wind tunnel test with a scale of 1/29. The TMD of lever and cantilever type were designed to test their vibration reduction efficiency. The results show that the critical flutter wind speed of the main girder is higher than that of the flutter test wind speed (104.4 m/s) at wind attack angle of 0°, ±3° and wind deflection angle of 0°, 15°, 30°, 45°, 60°, 90°; within the design reference wind speed (0~58.4 m/s), the main girder has vortex-induced vibration of first-order vertical bending, first-order torsion and second-order vertical bending at wind attack angle of 0°, ±3°and wind deflection angle of 0°, 15°, 30°. Compared with 0° wind attack angle, the wind speed lock range of first and second order vertical bending vortex-induced vibration has delay at +3° wind attack angle, and the amplitude decreases and increases, respectively; After TMD is installed, the locking range of vortex-induced vibration wind speed is almost unchanged, and the wind speed corresponding to the maximum amplitude decreases, the amplitude is reduced by 46%, 47% and 77%, respectively.
slotted variable section; foot bridge; flutter; vortex-induced resonance; eddy-current TMD
U448.27
A
1672 − 7029(2020)09 − 2296 − 07
10.19713/j.cnki.43−1423/u. T20191060
2019−11−29
国家自然科学基金资助项目(51478181,1534206)
牛华伟(1978−),男,河南驻马店人,教授级高工,从事桥梁抗风与TMD减振研究工作;E−mail:niuhw@hnu.edu.cn

(编辑 阳丽霞)
