一种基于分层抽样的大数据快速聚类算法
2020-10-15李顺勇张钰嘉彭晓庆曹付元刘恩乾
李顺勇 张钰嘉 彭晓庆 曹付元 刘恩乾
1(山西大学数学科学学院 山西 太原 030006) 2(山西大学计算机与信息技术学院 山西 太原 030006) 3(计算智能与中文信息处理教育部重点实验室 山西 太原 030006)
0 引 言
聚类分析是一种无监督算法,其目标是按照某种相似性度量将数据集中相似度较大的数据分到同一个簇,尽可能使簇内的数据相似性较大、簇间数据相似性较小[1-2]。聚类算法多种多样,可以从不同角度对算法进行分类,如根据层次、划分、密度等角度对其分类。如今处于大数据时代,数据量的增加以及数据本身的复杂化给聚类分析带来了不小的难度,一些面向于大型数据分类的算法被提出,本文针对各种算法可处理的原数据类型对其进行分类,如图1所示。

图1 聚类分类
传统方法中具有代表性的方法如K-means[3]、K-modes[4]、K-prototypes[5]、CURE[6]和DBSCAN[7]等。文献[3]提出了K-means算法,其距离度量函数面向的是数值型数据,所以在数据集比较复杂并且含有分类型数据时该算法存在一些不足。文献[4]提出了K-modes算法,该算法用modes代替means,在处理分类型数据时有较好效果。文献[5]提出了K-prototypes算法,利用简单匹配差异度来度量分类型数据距离,并且引入参数来刻画两种属性数据在距离度量时所占的权重。文献[6]提出的CURE算法可以识别一些形状比较复杂的簇,并且可以检测出数据中的一些异常点,但是该算法得到的结果不够稳定。文献[7]提出了基于密度划分的算法,提出了Density-reachability和Density-connectivity,该算法可以处理不同形状的簇,并且算法性能较好。文献[8]提出了一种智能聚类算法,该算法不需要计算结构化单分类器中的二次锥规划,只需要计算一个线性规划问题即可,从而节省了运算时间。文献[9]提出的算法降低了聚类运行时间,但是在处理分类型数据时该算法运行结果较差。文献[10]提出了一种高效率的处理大型数据的DBDC算法,该算法基本思想和DBSCAN算法相同,区别是DBDC算法是一种并行算法,效率远高于DBSCAN算法。文献[11]提出了一种基于稀疏编码的算法,该算法抽取一些数据点来逼近相似度矩阵,但是该方法得到的结果不稳定。文献[12]提出了一种并行算法,去掉了一些影响聚类质量的因素,如在输入数据时顺序的影响,并取得较好效果,其不足是不能处理混合数据。文献[13]提出了一种快速聚类算法,该算法结合了MapReduce分布并行计算框架,得到的结果较为稳定并且性能较好。
上述方法在处理大规模数据时会出现算法迭代时间长、聚类精度低等问题。为了在不影响聚类精度的前提下对数据进行快速有效的划分,本文提出了一种基于分层抽样的大数据快速聚类算法。该算法大致分3个步骤进行:(1)随机抽取μk个点(k为数据集簇数,μ为正数),随后在原始数据集上根据距离最小原则将剩余未抽到的数据划分到μk个点附近,得到μk个层,这样在进行抽样时可以覆盖数据的全局信息,降低初始点选取时的敏感性;(2)根据本文提出的抽样方案进行分层抽样,得到样本集;(3)用K-means算法对抽取的样本数据集进行聚类,得到划分结果。
1 K-means算法[3]
设一数据集为X={X1,X2,…,XN},X中共有N个数据,每个Xi有m个属性,即Xi={xi1,xi2,…,xim},设初始原型集合V={V1,V2,…,Vk},经过K-means算法得到的k个簇为C={C1,C2,…,Ck},其中C1∪C2∪…∪Ck=C且Ci∩Cj=∅。该算法的分类标准如定义1所示。
定义1[3]数据的分类标准为:
(1)
具体过程如算法1所示。
算法1[3]K-means算法
输入:原型k,数据集X。
输出:划分结果。
Step1选择k个原型V;
Step2根据式(1)将数据集中的各个样本分到各自所属的簇中,更新簇中心;
Step3计算原数据集中的数据和Step2中得到的簇中心的距离,根据式(1)对数据重新进行划分,并得出新的簇中心;
Step4重复Step2和Step3直到簇中心不再变化为止。
K-means算法由于其计算复杂度较小并且实现方便而得到广泛应用,但是K-means算法也存在一些不足之处:(1)在选取初始原型时采用的是随机选取原则,这样会造成算法结果不稳定,易受到初始原型选择的影响;(2)迭代次数较多,在处理数据量较大或者数据维数较高的数据时算法运行时间较长。
2 算法设计
基于上述K-means算法存在的一些不足,本文提出了FCASS算法。该算法将分层抽样与K-means算法结合,使其能在较短时间内输出正确率较高并且较稳定的划分结果。
为了使抽取出来的样本数据集有较好的代表性,确定抽取样本大小以及抽样方法尤为重要。基于此,本文还提出了一种分层抽样算法。
2.1 分 层
分层即将原始数据及分成不同层,使得同一个层内的数据相似度较大,不同层的数据相似度较小。K-means根据式(1)将数据分到距离其最小的k个初始点中,并且一直迭代,直到簇中心不变为止。首先选取h(h=μk,h 该分层技术优点较明显:(1)选取的初始点个数大于k,这样会降低分层时受初始点随机选择的影响;(2)只需要计算一次初始点和原始数据集中其他数据之间的距离,计算量小,节省时间。μ的具体取值会在仿真实验中求出。 本文采用文献[14]中的方法来得出合适的总样本数n: (2) 式中:S2为总体方差;Nh为第h层数据总数;Sh为第h层标准差。 (3) (4) 引进随机变量ai(i=1,2,…,N),若Yi被抽中,ai=1;反之,ai=0。 证毕。 (5) 由定义2可知: (6) (7) (8) 证毕。 定义4抽取样本的时间函数为: (9) (10) (11) 根据Cauchy-Schwarz不等式,对于任意ah≥0,bh≥0,有: (12) (13) 式(13)中等号成立的条件是: (14) (15) 假定各层的单位抽样时间相等,即th=t,得到每层抽取的样本数,计算公式如下: (16) 从式(16)可以看出,有较大WhSh的层会抽取较多的样本。Wh较大,意味着该层有较多的数据,所以应从该层抽取较多的样本;Sh较大,意味着该层数据分布较为分散,为了使抽到的样本能代表该层,故抽取的样本数也较多。 算法2FCASS算法 输入:原始数据集X,k个初始点。 输出:最终分类结果。 Step1选取h个初始原点,根据式(1)将数据集X分为h层; Step2根据式(2)计算要抽取的合理样本个数n; Step3根据式(15)计算出每层抽取的nh; Step4对每层进行抽样,得到样本集L={n1,n2,…,nh}; Step5对抽取的样本运行K-means算法,得到划分结果。 本文选取UCI数据库[15]的4个数据集以及8个人工数据集对算法性能以及运行速度进行评测,数据集形式如表1所示,其中:h表示属性数;class表示分类个数,即模k;instance表示样本个数。 表1 数据集信息 可以看出,Transfusion、Banknote、HTRU2以及Activity Recognition 4个数据集的instance相差较大,并且HTRU2和Activity Recognition数据集的h为9,维数较高,这样选取的数据集代表性较好,能较好体现算法在处理不同维度以及不同样本数的数据集时的性能。因此,本文生成的Artificial data也尽量增大数据集之间的差异性,如Artificial data 1到Artificial data 4数据集的h=3,但instance相差较大,并且与Artificial data 5到Artificial data 8的h相差较大,这样可以较全面地对算法性能进行测试。 本文选取AC、ARI[16]以及算法运行时间T作为评价指标。对数据集X={X1,X2,…,Xn},通过聚类划分得到的簇和在原始数据集中已有类标签划分得到的簇分别为C={C1,C2,…,Ck-1,Ck}和P={P1,P2,…,Pk′},定义AC和ARI计算公式如下: 式中:nCi和nPj分别是Ci和Pj中对象的个数,nij=|Ci∩Pj|。经过计算可知,0≤AC≤1,0≤ARI≤1,且AC、ARI值越接近1,划分效果越好。 确定参数μ的算法的具体过程见算法3。 算法3确定参数μ算法 输入:原始数据集X,初始点k。 输出:划分错误率。 Step1令μ=1,选取h=μk个初始点,根据式(1)将数据集X分为h层; Step2根据式(2)计算要抽取的合理样本个数; Step3根据式(16)计算出每层抽取的nh; Step4对每层进行抽样,得到样本集L={n1,n2,…,nh}; Step5对抽取的样本运行K-means算法,得到划分结果,并计算AC和ARI值; Step6令μ=2,3,…,重复上述步骤,并计算AC和ARI值。 选取表1中的Transfusion、Banknote和HTRU2 3个数据集进行实验,Transfusion数据集中有748个样本,Banknote数据集中有1 372个样本,HTRU2数据集中有17 898个样本,每个数据集的样本个数相差较大,这样可以使得出的结论更加可信。在三个数据集上运行算法3共10次,计算出AC和ARI值,实验结果如图2-图4所示。图中横轴表示的是μ的值,纵轴表示的是AC和ARI值,其值越大说明算法效果越好。 图2 Transfusion数据集不同μ值结果对比 图3 Banknote数据集不同μ值结果对比 图4 HTRU2数据集不同μ值结果对比 由图2可知,当μ=3时,在Transfusion数据集上AC和ARI值最大,故在该数据集上μ取3较为合适。 由图3可知,当μ=4时,在Banknote数据集上AC值最大,ARI值也最大,因此在Banknote数据集上μ取4较为合适。 由图4可知,当μ=5时,在HTRU2数据集上AC值最大,但是ARI值较小;μ=4时算法3输出的ARI值最高,AC值也较大。因此,考虑到算法运行时间以及AC值和ARI值,认为在HTRU2数据集上μ取4较为合适。综上,本文将μ定为4。 3.3.1真实数据集实验 本节选取表1中的Transfusion、Banknote、HTRU2以及Activity Recognition四个数据集,为了方便,本文将上述4个数据集的名称简写为TF、BK、HT2和AR。将本文算法的聚类结果与K-means算法结果作对比。上述4个数据集的h、class以及instance均相差较大,这样的实验结果具有较好的对比性,结果如表2所示。 表2 真实数据集结果对比 可以看出,在4个数据集上本文算法的AC值与K-means算法相差不大,HT2数据集和AR数据集上本文算法的AC值甚至略高于K-means算法,说明本文算法划分效果较好;在Transfusion和Banknote数据集上本文算法运行时间略长于K-means算法,但在HTRU2和Activity Recognition数据集上本文算法运行较快,结合表1中各个数据集的信息可以发现,当数据集的h较高以及instance较多时,本文算法运行速度较快。 3.3.2人工数据集实验 本节选取表1中的8个Artificial data进行实验,实验对比结果如表3所示。 表3 Artificial data实验结果对比 可以看出,在8个Artificial data上本文算法的AC值与K-means算法相差不大,这是因为本文抽取的样本具有较好的代表性。在8个Artificial data数据集上本文算法运行的时间均少于K-means算法,Artificial data中instance越多,本文算法运行速度的优越性体现得越明显,并且在数据集h增高时,本文算法运行时间远快于K-means算法。 结合表2和表3中的数据对比,本文算法在较高维度数据集以及大样本数据集上聚类效果优良并且算法运行时间较短。 本文提出了一种基于分层抽样的大数据快速聚类集成算法,该算法能够快速地处理较高维度以及大样本数据集,并且能够得到较高的聚类精度。本文算法的核心是分层抽样技术,其保证所抽取的样本具有较好的代表性。最后在4个UCI数据集以及8个人工数据集上进行仿真实验,结果表明在数据规模比较大时,本文算法有较高的聚类精度以及较短的运行时间,验证了本文算法的有效性。2.2 总样本量的确定
2.3 各层样本量的分配
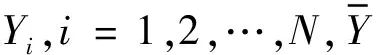



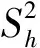

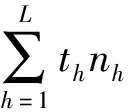
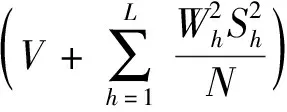

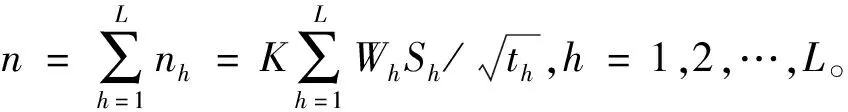
3 仿真实验
3.1 数据集的选择及评价标准
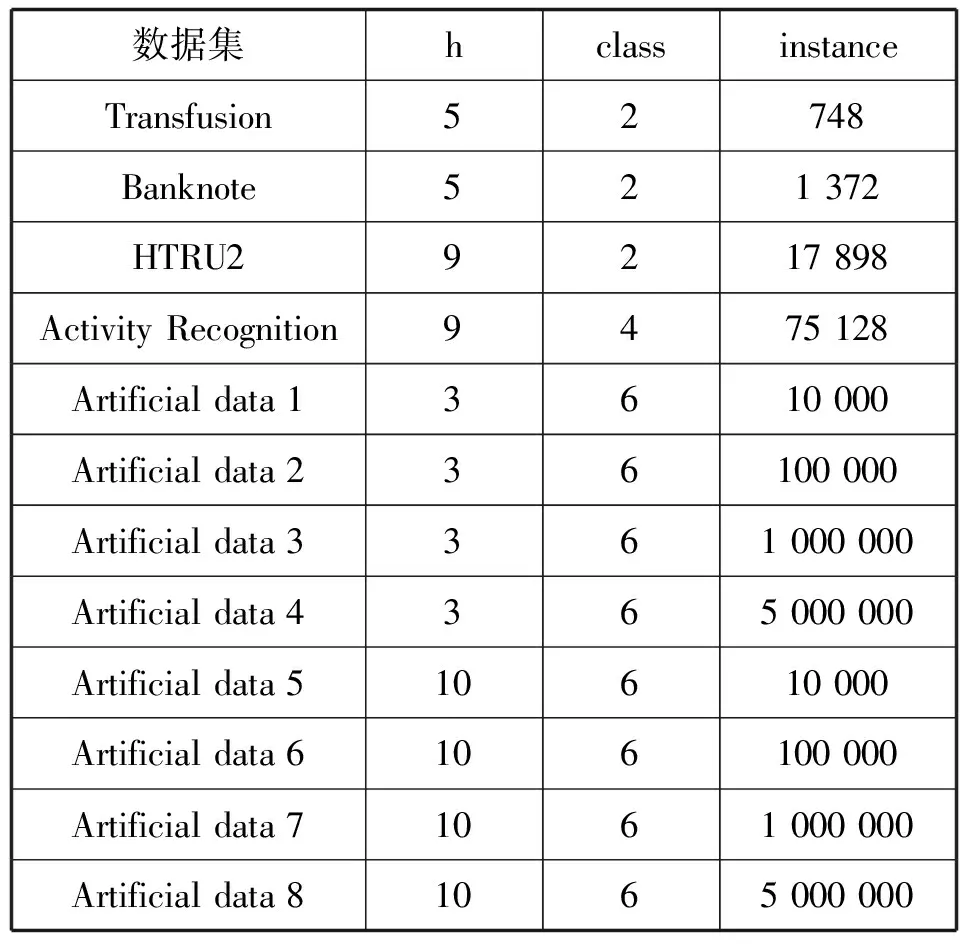
3.2 参数μ的确定



3.3 算法比较


4 结 语
