异质空间结构种群迁徙动力学优化算法*

黄光球，陆秋琴

西安建筑科技大学管理学院，西安 710055

1 引言

生态学理论认为，生物群落具有不顾干扰在空间持续生存的能力，有强烈地改善在空间分布状况的能力[1]。自然界中食物资源沿分布区往往相互镶嵌，这导致生物群落出现斑块分布。此外，在分布区出现混杂结构，生态学上称为斑块现象[2]。物种个体和种群空间镶嵌分布的结果也有类似的现象。若斑块中的生物个体有着各自不同的活动半径且不同物种的活动性有很大差异，种群规模具有非线性局部动态变化特征，种群迁徙受边界影响，这类结构称为异质空间结构[3]。

最早利用生物种群个体在不同斑块间迁徙这一自然现象构造出来的群智能优化算法[4-7]是生物地理学算法（biogeography-based optimization，BBO）[8]，该算法通过种群在斑块间的迁移实现了对优化问题最优解的搜索。BBO算法已在很多领域取得应用[9-13]。因BBO算法只有迁移、变异和精英保留三个算子，故目前绝大部分研究工作是针对这些算子的改进而提出的改进算法。文献[14]利用自适应差分算子改进BBO算法的迁移算子，该算子与原迁移算子相结合形成双迁移模式，从而使得BBO算法的性能得到提高；文献[15]利用差分扰动操作改进变异算子，垂直交叉操作改进迁移算子，从而提升了BBO算法的探索能力和求精能力；文献[16]利用差分算子改进迁移算子，趋优变异算子改进变异算子，从而提高了BBO算法的全局搜索能力，并平衡了其探索和求精能力；文献[17]用嵌入变异和细菌趋化现象的融合替换迁移算子，用贪婪选择算子替换精英保留策略，从而形成混合BBO算法。

此外，BBO算法的栖息地选择策略也是一个改进方向。文献[18]采用引力学习策略来选择栖息地，从而提出了一种基于邻域引力学习的BBO算法NFBBO（neighbor force-learning biogeography-based optimization）。文献[19]利用局部和全局自适应邻域校调策略来选择栖息地，从而提出了一种基于自适应邻域校调策略的BBO算法。

大量测试与应用表明[20-24]，BBO算法及其改进版存在如下问题：（1）该算法对维数较低的优化问题具有较好的性能，但当优化问题的维数很高，该算法的性能下降；（2）该算法的全局收敛性一直未被证明。出现上述问题的原因是BBO算法的迁移算子、变异算子和精英保留策略过于简单，无法适应复杂优化问题的求解。

为了解决上述问题，本文采用与BBO算法完全不同的理论基础，将BBO算法的理论基础即生物地理学理论改为群迁徙动力学理论，而将生物地理系统设定为具有异质结构特征，从而形成一种新型的群智能优化算法，称为异质空间结构种群迁徙动力学优化算法（optimization algorithm of population migration dynamics with heterogeneous spatial structure，HSS-PMDO）。由于这两种理论具有很大差别，因此本文提出的HSSPMDO算法与BBO算法及其改进版完全不同。

2 HSS-PMDO算法基本原理

考虑优化问题：

式中，X是一个n维向量；f(X)为目标函数；gi(X)为第i个约束条件，I为约束条件个数；Rn是n维欧氏空间；S为解空间；f(X)和gi(X)没有特殊的限制。

2.1 种群迁徙场景设计

假设某海岛上有N个生物种群在W个独立斑块中活动，这些斑块的编号集合为H={1,2,…,W}。假设斑块k上的种群集合为Pk，用种群编号表示为Pk=，k∈H，Nk表示斑块k上的种群个数。该。假设所有种群中的每海岛上种群总数为N=个生物个体具有特定的活动方式，能够从某一斑块迁徙到另一斑块。在同一时期，一个种群的个体能够在多个斑块上同时出现。

时期t，种群i在从斑块s到斑块k迁徙路线上的瞬时迁徙强度由下式决定[3]，即：

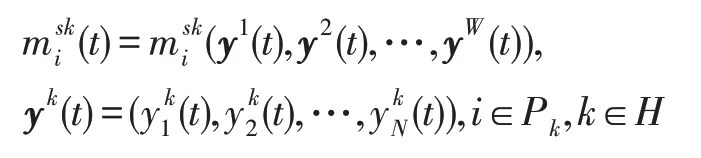
时期t，种群i中的生物个体数会受到迁徙的影响，其迁徙动力学模型为：

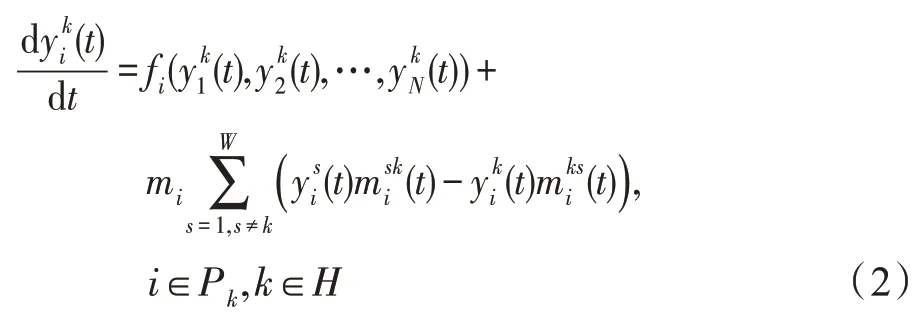
式中，mi为种群迁徙强度因子，mi≥0表示种群特异性和迁徙路线的独立性，mi=0表示种群i在所有斑块中都不参与迁徙。

对于海岛中的每个斑块，可选的生存条件集合SC={竞争型，互利型，捕食-被食型，融合型}。若种群i迁徙到斑块k，其对应的生存条件为Ek∈SC，则该种群以该斑块上的生存条件Ek生存。例如，假设斑块2的生存条件是捕食-被食型，种群1迁徙到斑块2上后，就会与该斑块上已有种群构成循环捕食-被食关系。

在海岛中，种群根据其所在斑块的状况及其个体的意愿决定是否迁徙。当某个种群发现本种群在当前所在斑块的密度过高或者生存适应度变差，则该种群随机选择一个斑块实施迁徙；当一个种群发生迁徙时，其迁徙规模是随机的。当一种群迁徙到新的斑块后，在该斑块要生存一段时间。经过一段时间后，种群再迁徙。如此重复，种群不断得到进化。

2.2 种群迁徙与生存策略

式中，ri称为种群i的内禀增长率；aij的正负符号和绝对值表示种群j对种群i的影响性质和强度。

多个种群在某斑块生活期间，其发展变化与所在斑块的生存条件相关。对于斑块k，有：

若斑块k的生存条件为竞争型，则认为种群间展开循环竞争活动。对于种群i∈Pk，依据式（3）可得Lotka-Volterra多种群间循环竞争动力学模型为：

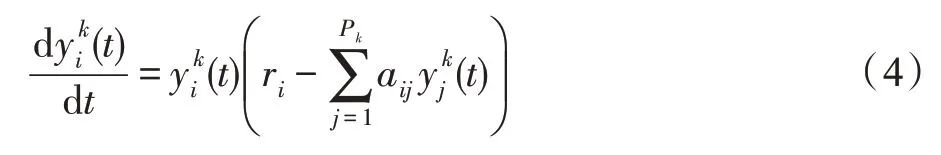
式中，aij＞0。

若斑块k的生存条件为互利型，则认为种群间展开循环互利活动。对于种群i∈Pk，依据式（3）可得Lotka-Volterra多种群间循环互利动力学模型为：

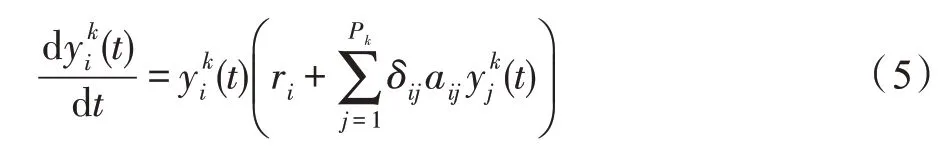
式中，若i=j，则δij=-1；若i≠j，则δij=1;aij＞0。

若斑块k的生存条件为捕食-被食型，则认为种群间展开循环捕食-被食活动。对于种群i∈Pk，依据式（3）可得Lotka-Volterra多种群间循环捕食-被食动力学模型为：

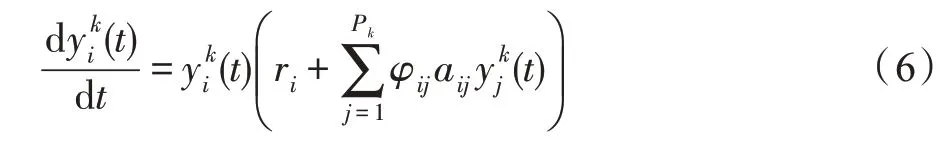
式中，若i=j或j=i+1，则φij=-1；否则，φij=1;aij＞0。

2.3 优化问题与海岛的对应关系

优化问题的解空间与海岛相对应，每个种群对应着优化问题的一个试探解，种群的一个特征对应于试探解中的一个变量。时期t，海岛中斑块k的Nk个种群所对应的优化问题的试探解集为；种群i的特征j与试探解的变量相对应；种群i的强壮度指数与优化问题（1）的目标函数值的转换关系为：

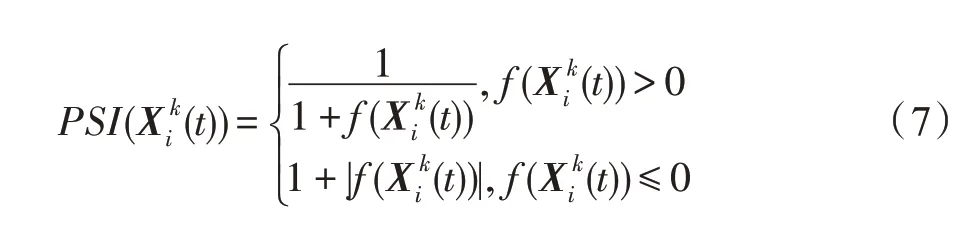
海岛上的一个斑块的生存适应度（individual suitability index，ISI）描述了该斑块的生存环境好坏，生存环境好的斑块具有较高的ISI值。时期t，斑块k的生存适应度ISI(k,t)可用其上活跃的种群的平均强壮度指数（population suitability index，PSI）来描述：

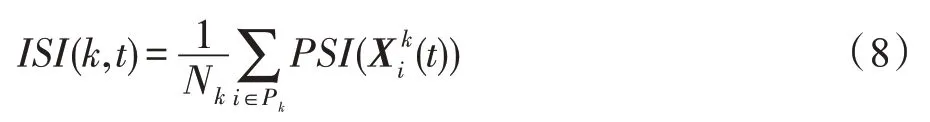
2.4 种群进化算子设计

2.4.1 斑块上种群规模计算方法

（1）因种群迁徙导致的种群规模变化（迁徙算子）。假设种群i生活在斑块k上，k∈H，该种群想迁徙到斑块s上，依据式（2），斑块k和s上的种群规模发生如下变化：

（2）因种群间竞争导致的种群规模变化。若斑块k的生存条件为竞争型，则依据式（4），斑块k上的种群i∈Pk的规模发生如下变化：

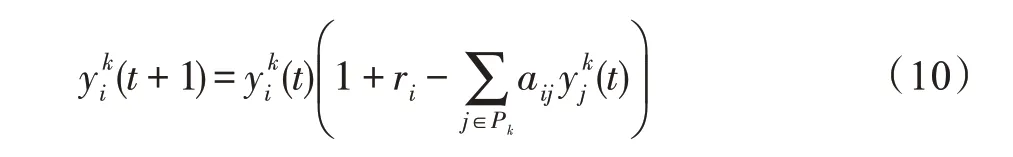
（3）因种群间互利导致的种群规模变化。若斑块k的生存条件为互利型，则依据式（5），斑块k上的种群i∈Pk的规模发生如下变化：

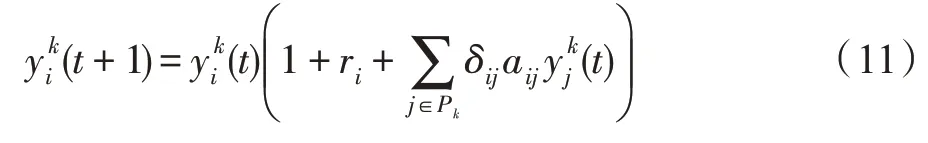
（4）因种群间捕食-被食导致的种群规模变化。若斑块k的生存条件为捕食-被食型，则依据式（6），斑块k上的种群i∈Pk的规模发生如下变化：

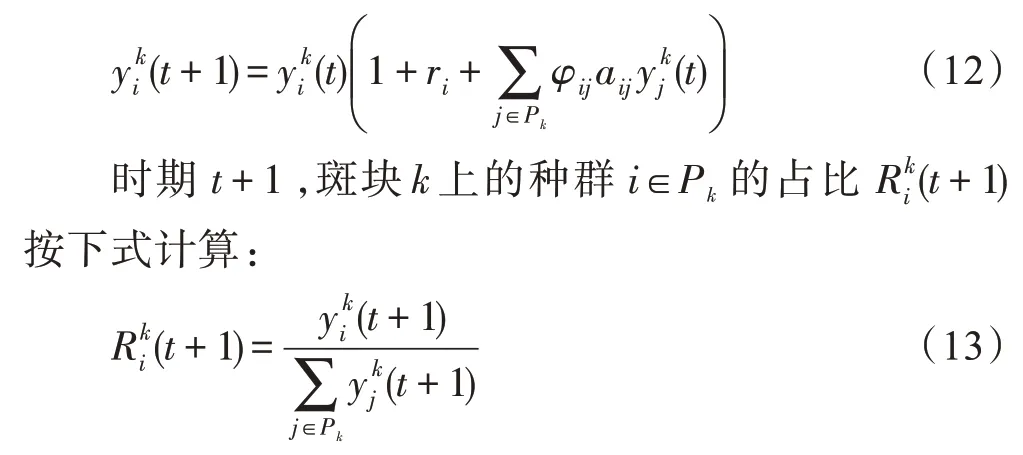
2.4.2 特征种群选择

（1）普通种群集GSk的产生方法：从生活在斑块k的Nk个种群中随机挑出M个种群，但当前种群i∈Pk不包括在内，形成普通种群集合{a1,a2,…,aM}⊆Pk。

（2）优势种群集PSk的产生方法：从生活在斑块k的Nk个种群中随机挑出M个种群，这些种群的PSI指数要比当前种群i∈Pk高，形成优势种群集PSk=

（3）强势种群集QSk的产生方法：若当前种群为i∈Pk，则从生活在斑块k的Nk个种群中按照PSI指数和占比要比当前种群i高，形成强势种群集QSk=

2.4.3 演化算子设计

（1）竞争算子。若斑块k的生存条件为竞争型，则对于当前种群i∈Pk，k∈H，有：

式中，βs=Rnd(0.4,0.6)，αs=Rnd(0.6,0.9)，λs=Rnd(0.4,0.7)，p=Rnd(0,1)；j为从{1,2,…,n}中以概率E0随机选择的一个数，E0为特征影响概率；Rnd(a,b)表示在[a,b]区间产生的一个均匀分布的随机数。

（2）互利算子。若斑块k的生存条件为互利型，则对于种群i∈Pk，k∈H，有：

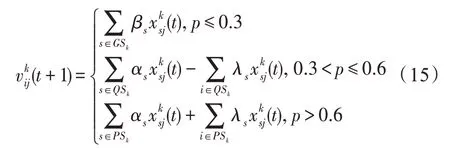
（3）捕食-被食算子。若斑块k的生存条件为捕食-被食型，则对于种群i∈Pk,k∈H，有：

（4）选择算子。将新一代种群与相应的父代种群进行比较，较优者保存到下一代种群中，即：

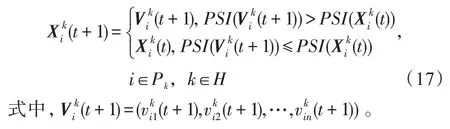
2.5 HSS-PMDO算法设计

HSS-PMDO算法包括如下步骤：

（1）初始化：①令时期t=0，按第3章介绍的方法初始化本算法涉及到的所有参数。②将N个种群随机分配给W个斑块，使得W个斑块上的种群数分别为N1,N2,…,NW；各斑块上的种群编号的集合分别为P1,P2,…,PW；在生存条件集合SC中随机选择一个生存条件指定给每个斑块，其结果是：W个斑块的生存条件分别为E1,E2,…,EW。③随机确定每个斑块上的所有种群的生物个体数量，i∈Pk,k∈H。④随机确定初始解，i∈Pk,k∈H；随机确定Z*，Z*用于记录当前全局最优解。

（2）执行下列操作：。

2.6 时间复杂度估计

HSS-PMDO算法的时间复杂度计算过程如表1所示。

2.7 算法的收敛性分析

（1）Markov特性。从各算子式（14）～式（16）的定义知，时期t+1的任意新试探解的计算生成只与其在时期t的状态有关，而与其以前是如何演变到当前状态的历程无关，表明HSSPMDO算法的演进过程具有Markov特性。

（2）“步步不差”特性。从选择算子的定义式（17）知，时期t+1，对任一种群均有表明HSS-PMDO算法的演进过程具有“步步不差”特性。

（3）HSS-PMDO算法全局收敛性。利用HSSPMDO算法的Markov特性和“步步不差”特性，可以证明HSS-PMDO算法的全局收敛性，其证明过程可参见文献[25]。

3 HSS-PMDO算法的最佳参数确定

HSS-PMDO算法的参数由两部分组成，一部分是与异质空间结构种群迁徙动力学理论有关的参数，它们是mi、、ri、aij；另一部分是与算法时间复杂度相关的参数，即G、ε、W、M、N(N1,N2,…,NW)、R0、ISI0、E0。这些参数的确定方法如下：

（1）参数mi、、ri、aij的设置方法。这些参数由异质空间结构种群迁徙动力学理论确定，是本算法的内置参数，只要设置一次即可，无需修改。这些参数的设置方法如下[3]：

采用上述参数设置方法，可保证迁徙的种群分布具有很好的异质性，而种群中的生物个体数具有很好的随机性[3]。

（2）参数G、ε、W、N(N1,N2,…,NW)、R0、ISI0、M、E0的确定方法如下：

①无需精确设置的参数G、ε的设置方法。G的取值依据是为了防止迭代过程不满足收敛条件时出现无限迭代，G=8 000～100 000；ε越小，所获得的最优解的精度越高，但计算时间越长，可取ε=10-5～10-10。

②可自动调整的参数R0、ISI0的设置方法。参数R0、ISI0用来控制种群迁徙的强度，种群迁徙强度会影响种群特征的变化水平，这些参数可采用下列方法进行自动动态设置：

③需根据实际情况进行设置的参数W、N(N1,N2,…,NW)、M、E0的设置方法。W相当于给种群分类，W越大，种群多样性越好，算法探索能力越强，陷入局部最优陷阱的概率越低，但计算时间越长；N(N1,N2,…,NW) 控制着任意斑块上种群数，可取N1=N2=…=NW=N/W，故只要确定N和W的取值规律，即可确定N1,N2,…,NW；M和E0用来控制种群特征的变化范围和程度。

综上所述，HSS-PMDO算法需要人工根据实际情况进行设置的关键参数只有N、W、M和E0，下面以著名的BUMP优化问题[26]为例来确定N、W、M和E0的取值规律，该问题与工程实际问题较类似，其数学模型为：

表2描述了当N=200，W=10，E0=0.01，n=50，G=8×105时，参数M与平均最优目标函数值（Favg）和平均计算时间（Tavg）之间的关系。它表明，当M增加，Tavg和Favg的精度均不产生明显的变化。因此，M=3～6比较合适。

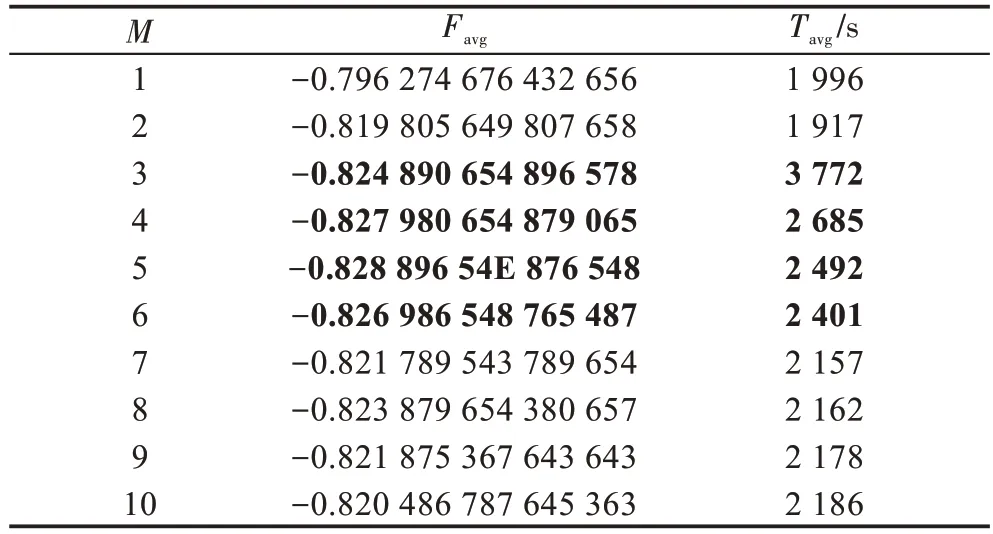
Table 2 Relationship of parameter M with Favg and Tavg表2 参数M 与Favg 和Tavg 之间的关系

表3描述了当N=200，W=10，M=3，n=50，G=8×105时，参数E0与Favg和Tavg之间的关系。结果表明，当E0=0.001～0.080，精度比较高，但CPU时间增加适度；当E0＞0.08，CPU时间相差很大，但精度也大大降低；尤其当E0=1时，它无法获得最优解。因此，当E0＝0.008～0.080时，HSS-PMDO算法性能最好，此时意味着最多只有0.008～0.080变量参与运算。

表4描述了当W=10，M=3，E0=0.01，n=50，G=8×105时，参数N/W与Favg和Tavg之间的关系。结果表明，当N/W=10～30，精度比较高，但计算时间增加不多。

表5描述了当W=10，N/W=20，M=3，n=50，G=8×105时，E0、n、Favg和Tavg之间的关系。从表5可以看到：当n增加时，Tavg大大增加；对于给定的n，如果E0增加，Favg的精度会降低，但Tavg增加。因此，如果n≥300，E0可取小值，如E0=0.001；如果n＜300，E0可取大值，如E0=0.01～0.04。

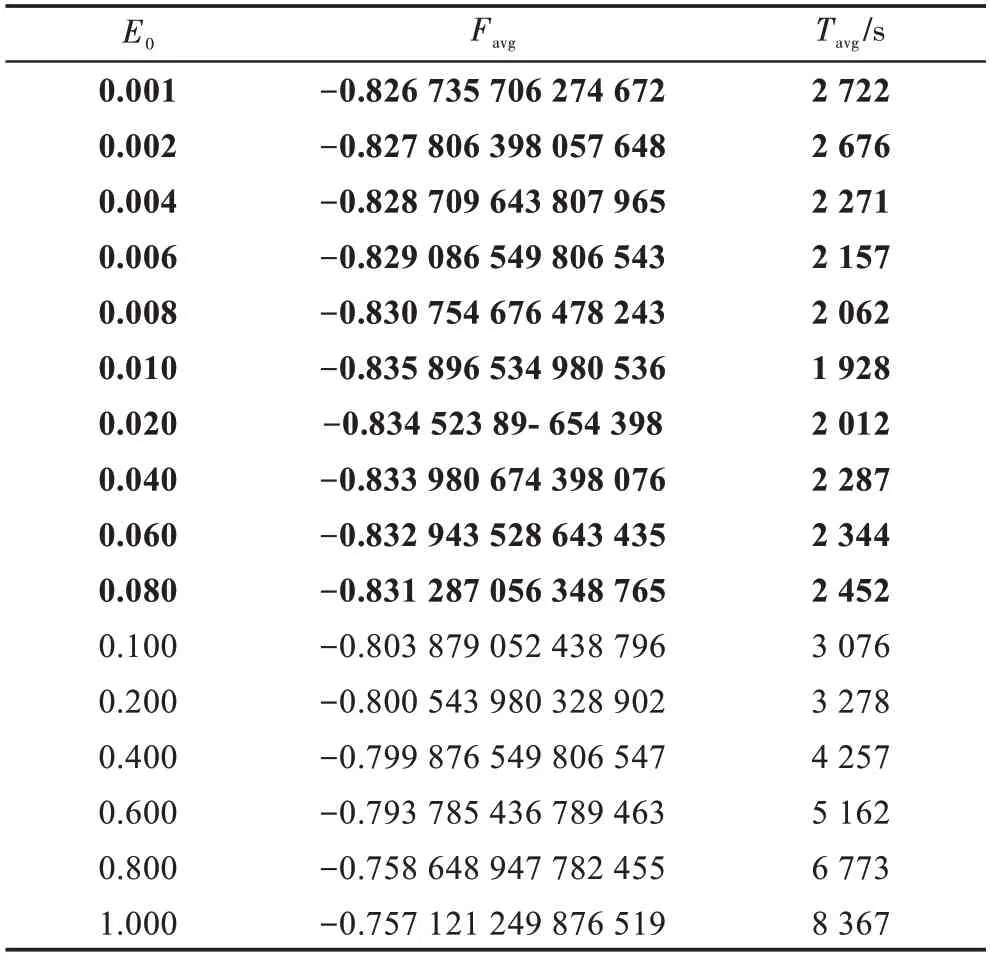
Table 3 Relationship of parameter E0 with Favg and Tavg表3 参数E0 与Favg 和Tavg 之间的关系

Table 4 Relationship of parameter N/W with Favg and Tavg表4 参数N/W 与Favg 和Tavg 之间的关系

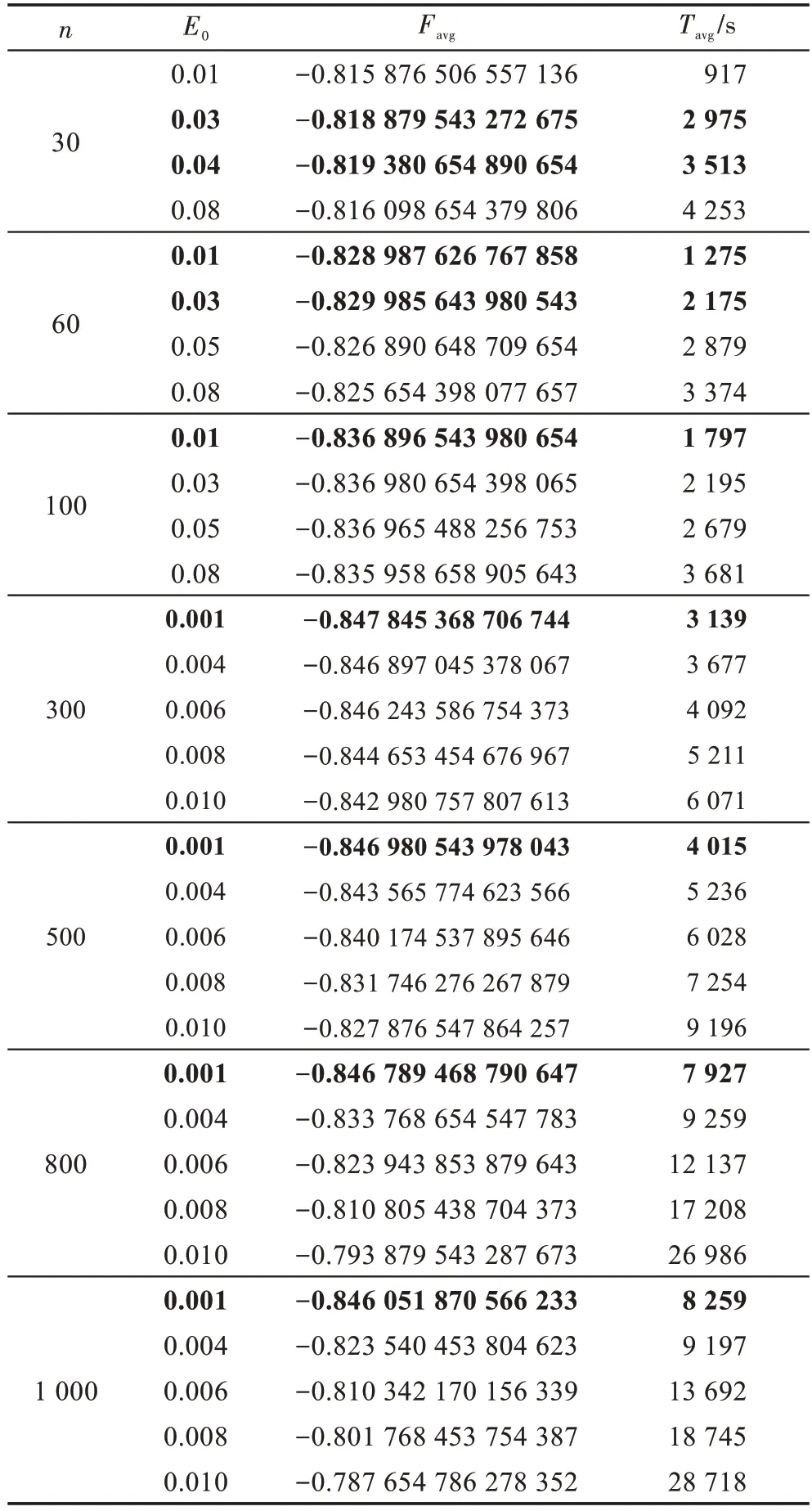
Table 5 Relationship among parameter n,E0, Favg and Tavg表5 n、E0、Favg 和Tavg 之间的关系

4 与其他群智能算法的比较

本文选用测试包CEC2013[27]中所提供的10个基准函数优化问题来测试HSS-PMDO算法的性能，如表6所示。

表6中O是可以任意设定的理论全局最优解，其维数为n。F15、F22、F23、F26、F28的理论全局最优解目前尚未发现。本文用HSS-PMDO算法求解表6中的10个基准函数优化问题，其参数是W=10，N/W=20，M=3，E0=0.01，n=50，G=8×105，ε=10-7。与HSS-PMDO算法进行比较的7个最新改进型BBO算法为DBBO[28]（disruption in biogeography-based optimization）、HBP-FNN+WE[13]（hybrid biogeographybased presentation with fitted nearest neighbor and widest exploration）、B-BBO[29]（blended biogeographybased optimization）、CARC-BBO[30]（chaotic adaptive realcoded biogeography-based optimization）、MpBBO[31]（metropolis biogeography-based optimization）、RCBBO[32]（real-coded biogeography-based optimization）、HBBO[33]（hybrid biogeography-based optimization）。其中DBBO算法通过修改BBO算法的迁移和变异两个算子并引入一个中断算子，可以显著提高BBO算法的探索和求精能力。HBP-FNN+WE算法是在BBO算法中采用一种新的方法来描述候选解，并将该表达法和局部搜索相结合，从而提高算法性能。B-BBO算法对BBO算法进行两次扩展：一是提出了一个混合迁移算子；二是通过修改BBO算法的迁入和迁出机制来处理约束，该算法不需要任何额外的调整参数。CARC-BBO算法采用基于混沌自适应实数编码来改进BBO算法。MpBBO算法采用BBO算法与模拟退火算法SA（simulated annealing）相结合的方法，以改善BBO算法的性能，该算法通过SA的Metropolis准则选择下一个迁移岛。RCBBO算法是一种采用基于实数编码的BBO算法。HBBO算法是一种将进化算法EA（evolution algorithm）和BBO算法相结合的算法。该算法包括两种杂交方法：一是迭代级杂交，其中各种EA和BBO按顺序执行；二是算法级杂交，它独立运行各种EA，然后利用BBO的思想在它们之间交换信息。这7个算法的参数设置可参见文献[28-33]，求解优化问题时的终止运行条件与HSS-PMDO相同。

Table 6 10 benchmark function optimization problems表6 10个基准函数优化问题

针对表6中列出的10个优化问题，用HSSPMDO算法和7个被比较算法进行求解，每个算法均独立求解51次，表7给出了求解结果。

表7中总排名1是这8个算法基于平均最优目标函数值进行的排名，总排名2是这8个算法基于平均最优目标函数值和适应度评价次数进行的排名；最终总排名1和最终总排名2是分别基于总排名1和总排名2所进行的排名。

Table 7 Solution results表7 求解结果

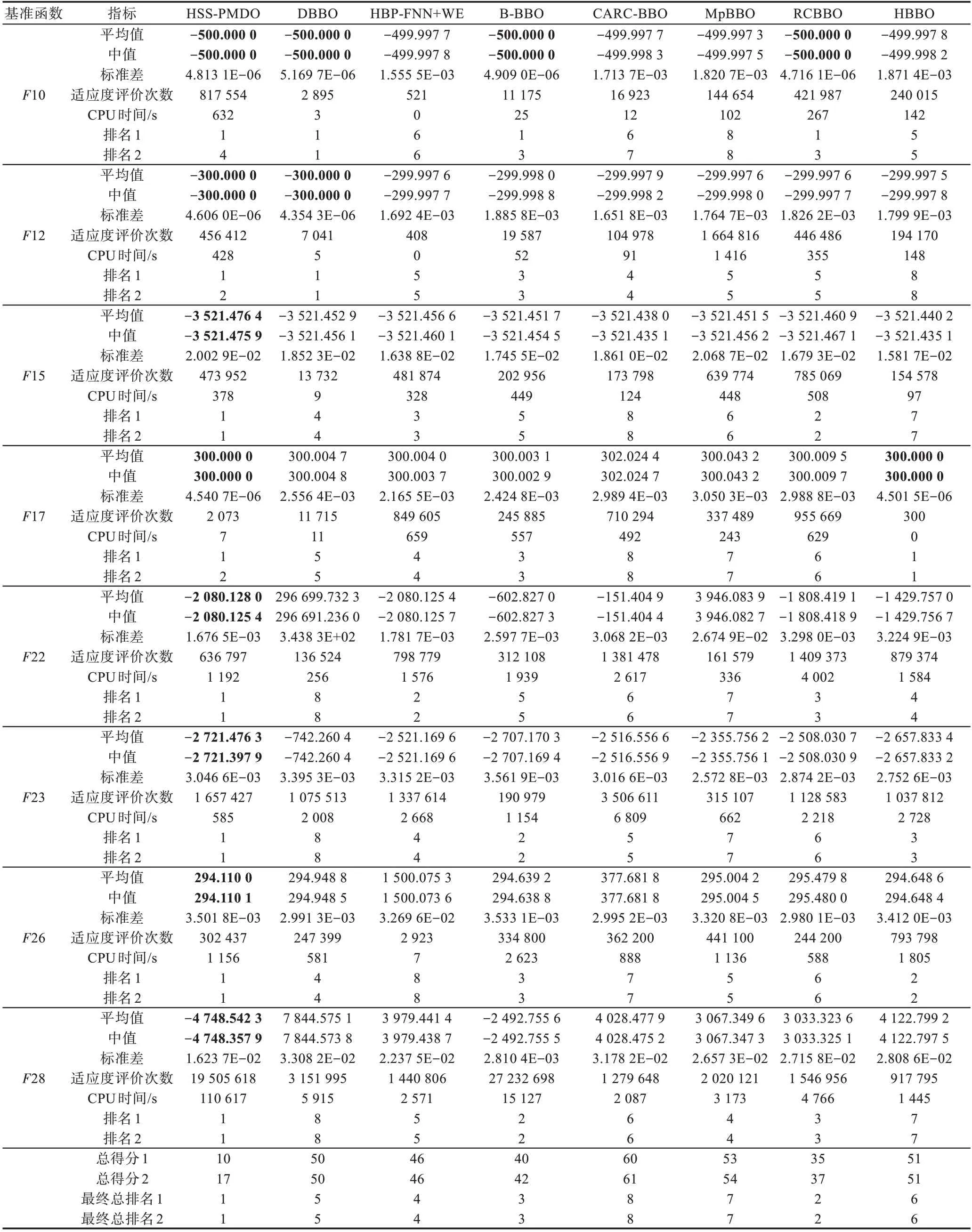
续表

从表7可以看出，对7个算法进行排序所得的结果均为：

HSS-PMDO＞RCBBO＞B-BBO＞HBP-FNN+WE＞DBBO＞HBBO＞MpBBO＞CARC-BBO

图1（a）～图1（j）给出了各个算法求解时的样本收敛曲线，其中的水平和垂直轴采用对数刻度。

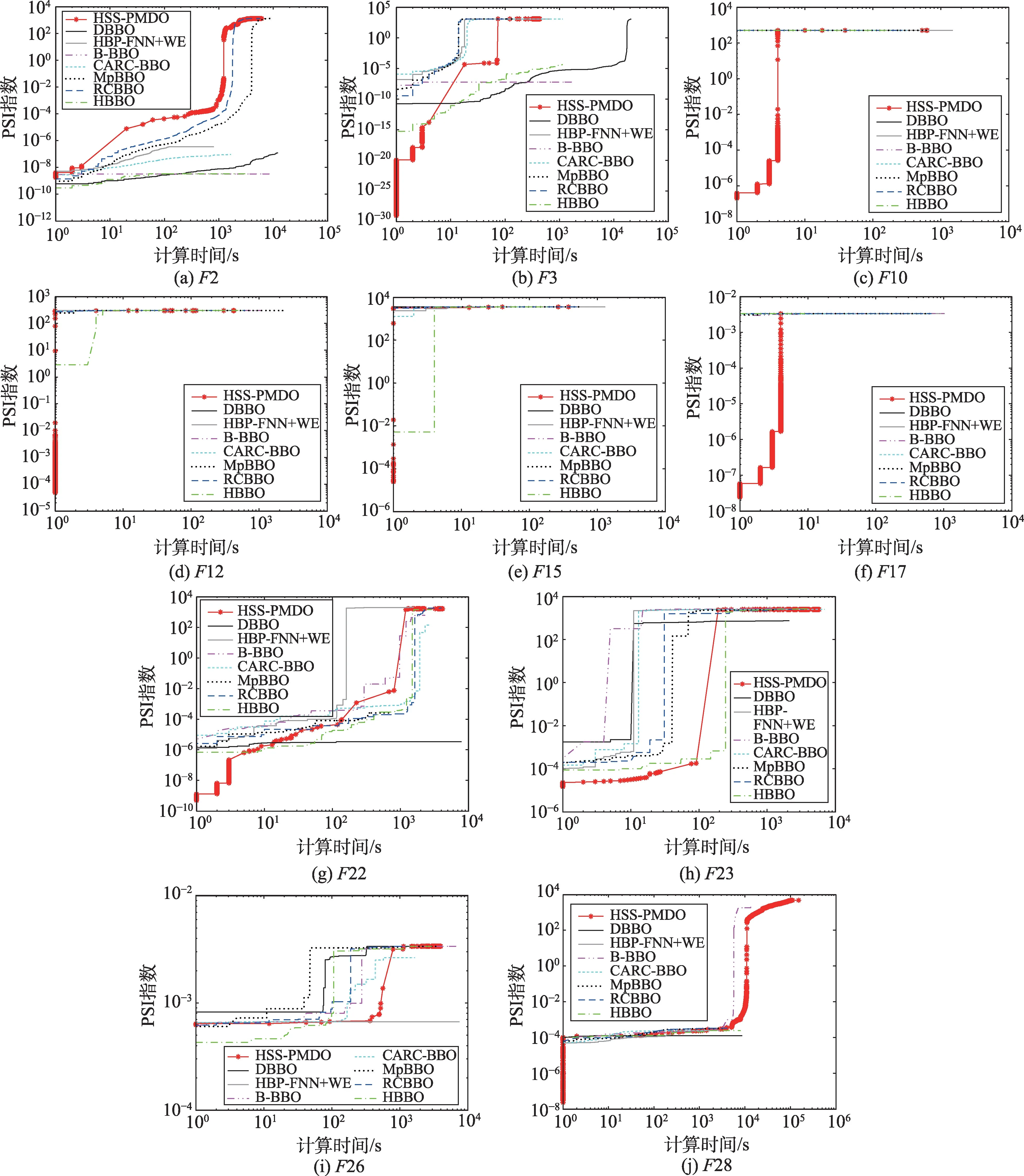
Fig.1 Sample convergence curves图1 样本收敛曲线

5 算法的性能分析

5.1 算子的性能分析

在HSS-PMDO算法中，只要每个斑块上的任意一个种群的规模发生变化，其生存条件对应的算子就会被执行。当HSS-PMDO算法求解F3时，随机选择斑块3、5、8，其对应的生存条件分别为竞争型、互利型和捕食-被食型，图2描述了竞争、互利和捕食-被食算子被触发执行的次数与CPU计算时间之间的关系。从图2可知，每种算子被触发执行的次数随CPU计算时间随机变化，但平均触发执行次数接近于水平，表明竞争、互利和捕食-被食算子几乎被均匀触发执行。

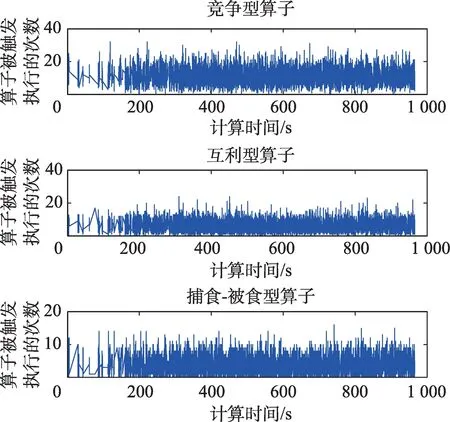
Fig.2 Relationship between the number of times the operator is triggered to run and CPU time图2 算子被触发执行的次数与CPU时间之间的关系

5.2 种群的动态行为分析

为了分析种群的动态行为，当使用HSS-PMDO算法求解基准函数F3时，随机选择种群27实施追踪，图3描述了种群27在搜索空间进行搜索时的运动轨迹。从图3可以看出，种群27并没有朝着更坏的方向移动，因为该种群对应的PSI指数一直在增加。

5.3 求精能力、探索能力及其平衡性分析

Fig.3 Moving track of population 27图3 种群27的移动轨迹

（1）求精能力分析。求精能力描述了HSSPMDO的算子在局部区域内（即某个邻域）提升最优解精度的能力，表现方式是个体在其收敛曲线上的某些区段以近似水平方式缓慢提升最优解的精度。图4描述了当HSS-PMDO算法求解F2时，各个算子被调用的情况。从图4可以看到，只要收敛曲线出现近似水平发展态势，竞争算子被执行的次数明显高于互利算子和捕食-被食算子。此现象表明竞争算子主要负责HSS-PMDO算法的局部区域求精。

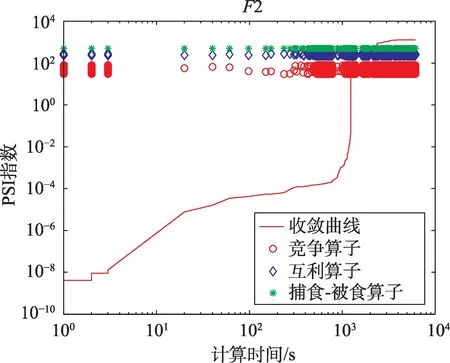
Fig.4 Analysis on ability of exploitation,exploration and their balance图4 求精能力、探索能力及其平衡性分析

（2）探索能力分析。探索能力描述了HSS-PMDO算法探索新空间的能力，表现方式是个体在其收敛曲线上的某些区段以倾斜向上的方式快速更新最优解。从图4可以看到，只要收敛曲线出现以倾斜向上的发展态势，竞争算子被执行的次数明显降低，互利算子和捕食-被食算子执行的次数不断增多。此现象表明互利算子和捕食-被食算子主要负责HSSPMDO算法的新空间探索，这两个算子只需被调度执行较少次数，就可以快速探索出新空间，其执行效率很高。

（3）求精和探索能力的协调性分析。从图4可知，HSS-PMDO算法求解F2时，其收敛曲线的缓（求精能力）和陡（探索能力）交替出现，且缓的持续时间少于陡的持续时间，此表明HSS-PMDO算法的求精和探索能力的协调性很好。

6 结束语

本文依据生活在某海岛上的生物种群在各斑块之间的迁徙行为，采用种群迁徙动力学理论提出了HSS-PMDO算法，该算法具有如下特征：

（1）HSS-PMDO算法采用与BBO算法完全不同的设计思路，即BBO算法采用的是生物地理学理论，而HSS-PMDO算法采用的是种群迁徙动力学理论，这两种理论存在很大差别。

（2）算法参数设置根据充足，需要人工依据实际情况设置的参数较少。算法中参数分为四部分，即依据种群迁徙动力学理论进行设置的内置参数、依据演化进程自动进行调整设置的参数、无需精确设置的参数、依据优化问题的实际情况需人工设置的参数，需人工设置的参数只有四个。

（3）各算子分工明确。HSS-PMDO算法包括迁徙算子、竞争算子、互利算子、捕食-被食算子和选择算子，这些算子大幅增加了其搜索能力。其中，竞争算子可提升算法的求精能力；互利算子和捕食-被食算子负责提升算法的探索能力；迁徙算子负责种群的多样性动态调整，使得种群间信息交换充分，从而提升了探索能力和求精能力的平衡性；选择算子可确保算法具有全局收敛性。

（4）通过自动降维方式提升算法收敛速度和对求解较高维数优化问题的适应性。因HSS-PMDO算法每次进化时仅涉及到种群的极少部分特征（0.1%～8.0%）的信息更新，即当种群间交换信息时，只有极少一部分特征参与运算，故本文算法收敛速度快，具有求解维数较高的优化问题的能力。

（5）具有全局收敛性。HSS-PMDO算法所涉及的演化过程能充分体现种群迁徙动力学理论的基本特征，演化过程具有Markov特性和“步步不差”特性，从而确保HSS-PMDO算法具有全局收敛性。

本文算法下一步需要改进的方向：

（1）进一步利用种群迁徙动力学理论优化HSSPMDO算法的相关参数，使得这些参数设置更合理。

（2）深入研究种群迁徙算子、竞争算子、互利算子、捕食-被食算子的动态特征。

（3）深入研究HSS-PMDO算法求解过程中各斑块的动态特征。

（4）依据种群迁徙动力学理论的变种，对HSSPMDO算法进行改进。

（5）将BBO算法的一些特征，融入到HSSPMDO算法中。