基于SMOTE 算法和动态代理模型的船舶结构可靠性优化

刘婧，王德禹*

1 上海交通大学 海洋工程国家重点实验室，上海 200240

2 高新船舶与深海开发装备协同创新中心，上海 200240

0 引 言

结构可靠性是指结构系统在规定的使用条件与环境下，在给定的使用寿命期间，能有效承受载荷和耐受环境影响并保持正常工作的概率。通过结构可靠性研究，可以提升结构性能，降低维修风险，这对于高可靠、长寿命和昂贵的结构制造而言具有重要意义。在船舶海洋结构物设计中，由于结构尺寸、材料性能和环境等包含有大量不确定的因素，而可靠性优化设计可以同时保证结构的经济性和安全性，是极具优势的优化设计方法，因而被广泛应用于船舶、飞行器、汽车设计等领域[1-3]。

可靠性优化设计最直接的解决方法是建立两层次优化问题，外层为设计变量的优化迭代，内层为结构可靠性评估[4]。由于两层次算法是高度非线性的耦合问题，因此存在计算量大、效率低等缺点。针对该问题，Liang 等[5]提出了一种单层次算法，该方法通过计算极限状态函数的可靠性指标，可近似得到结构的最小功能点，称为单循环算法（single loop algorithm，SLA）；贺谦等[6]使用SLA 法对涡轮叶片进行了可靠性及多学科优化，将概率约束优化问题转换为近似的确定性约束优化问题求解，显著提高了计算效率。在可靠性优化设计中，迭代次数较多，使用有限元模型（FEM）计算虽然计算精度高但会耗费巨大的时间成本，计算效率十分低下，因此，可采用准确的代理模型代替有限元计算来拟合设计变量与响应之间的关系。常见的几种代理模型有多项式响应面模型（PRS）、Kriging 模型、径向基函数模型（RBF）、支持向量回归（SVR）、BP 神经网络模型等，其中BP 神经网络模型可以较好地模拟非线性映射问题，适合代替计算耗时的大型有限元模型[7]。

根据构造方式的不同，代理模型可以分为2 种：静态代理模型和动态代理模型[8-9]。静态代理模型是通过采样获取足够多的样本点来构造代理模型，并且该代理模型在优化过程中始终保持不变。为了提高静态代理模型的近似精度，需要在整个设计空间中分布较多数量的样本点，但这会使调用分析计算模型的次数增多，优化效率降低。动态代理模型是在优化迭代的过程中不断更新样本点，并重新构造代理模型，直至优化迭代收敛。与静态代理模型相比，动态代理模型具有更高的优化效率和结果精度。Wang[10]提出了自适应响应面方法（adaptive response surface method，ARSM），该方法是一种基于响应面法（RSM）的动态代理模型方法，具有很好的全局收敛性与优化效率。彭磊等[8]提出了重点采样空间的概念，即在优化过程中逐步更新重点采样空间并在其内部增加样本点然后更新代理模型，从而建立动态径向基函数代理模型。Li 等[11]提出了一种基于序列代理模型的可靠性优化方法，其是通过初始样本点建立代理模型以后，再通过一系列的优化问题来增加初始最优解附近的样本点，从而更新代理模型，提高代理模型精度。Meng 等[12]将Kriging模型与自适应混沌单循环方法相结合，通过在目标可靠面上沿下降的方向增加样本点，提高了最可能失效点（MPP）附近局部区域的代理模型精度。

由结构可靠性理论可知，MPP 附近区域对失效概率的贡献最大。Echard 等[13]通过调用失效面附近的样本点建立代理模型计算了失效概率，结果显示计算效率很高，且非常适用于高可靠度模型。龙周[14]通过引入少数类合成的过采样算法（synthetic minority over-sampling technique，SMOTE）计算敏感域，使BP 神经网络模型高效、准确地近似极限状态函数，提高了优化效率与精度。SMOTE算法是一种利用现有样本集，对少数类样本进行“过抽样”而合成新样本的机器学习算法[15]。本文将引入SMOTE 算法来增加当前最优解周围失效面附近的样本点。

针对船舶结构可靠性优化中的高度非线性问题，本文拟提出2 个优化策略：一是通过在优化过程中使用SMOTE 算法，逐步增加当前最优解周围失效面附近的样本点，并更新BP 神经网络模型，以在全局最优解附近更好地近似极限状态函数；二是在可靠性优化的SLA 算法中采用模拟退火法（ASA）和动态BP 神经网络模型，以保证可靠性优化计算结果的准确性和高效性。

1 基 于SMOTE 算 法 和 动 态BP 神经网络的可靠性优化方法

1.1 BP 神经网络模型简介

1.2 SMOTE 算法原理简介

可见，SMOTE 算法的采样是在少数类样本点与其近邻样本点的连线上进行随机插值，即直线插值，新生成的少数类样本点具有通用性，相比单纯地复制原始样本点，SMOTE 算法能够对不平衡数据进行更好的处理。在船舶结构可靠性优化中，位于失效面附近的样本点数量非常少，而该区域的样本点对于失效概率的贡献最大，因此，要准确拟合失效面函数，需要合成少数类的样本点，故SMOTE 算法适用于船舶结构可靠性优化计算。

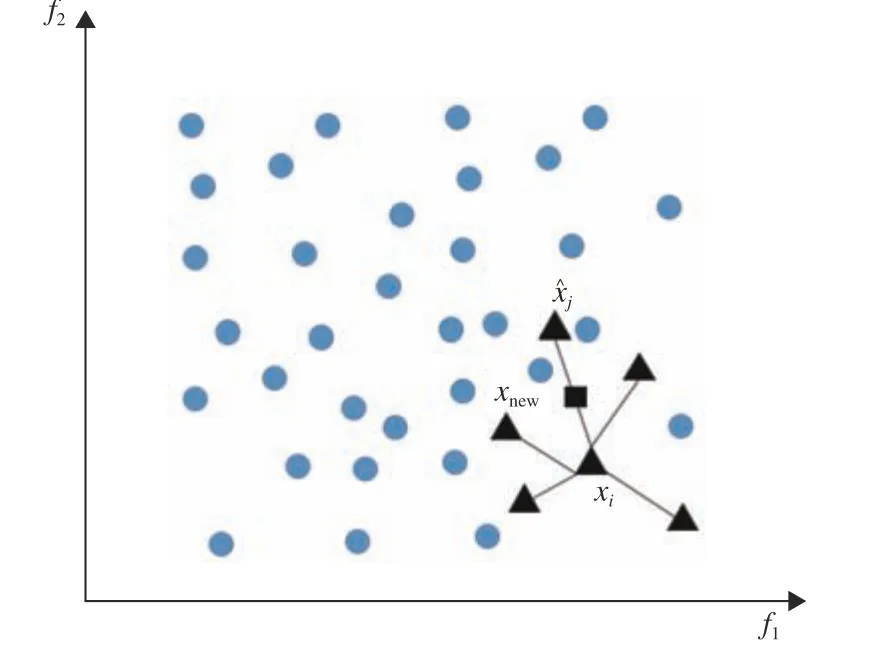
图1 SMOTE 算法合成少数类样本示意图Fig. 1 Schematic diagram of synthesizing minority samples by SMOTE algorithm

1.3 SLA 简介

SLA 的基本原理是，通过将可靠性循环的Karush-Kuhn-Tucker 最优性条件作为等效的确定性设计优化公式的约束，将概率优化问题转换为等效的确定性优化问题。采用SLA 进行可靠性分析能避免计算最可能失效点时的反复优化迭代过程，极大地提高了计算效率，同时还具有与两层次算法同等的计算精度[18]。SLA 的数学模型可以描述为[5]：

1.4 基于SMOTE 算法和动态代理模型的可靠性优化

对于一般结构，特别是具有高度非线性的船舶结构，本文提出的基于SMOTE 算法和动态代理模型的可靠性优化方法的基本思路是：首先，采用最优拉丁超立方试验设计在设计空间中产生均匀分布的初始样本点，调用有限元计算得到响应值，加入训练集，建立初始的BP 神经网络模型；然后，利用ASA 和可靠性优化设计的SLA 找到当前全局最优解以及最优解周围 k个位于失效面附近的样本点，通过SMOTE 算法增加最优解周围的样本点，更新代理模型以提高其在全局最优解附近的精度，并判断是否满足收敛条件，若不满足，则继续迭代。

基于SMOTE 算法和动态BP 神经网络模型的可靠性优化策略流程图如图2 所示。

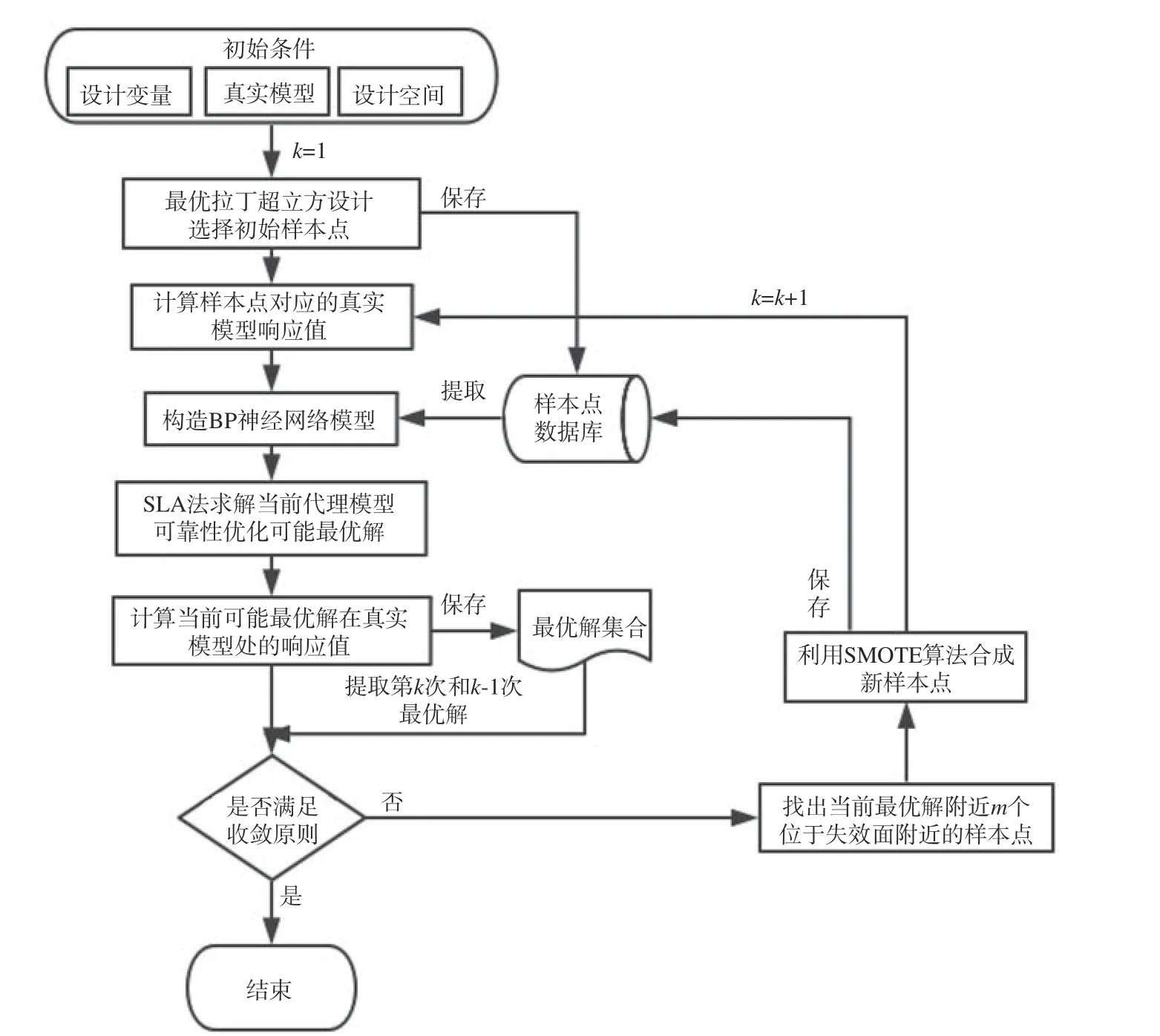
图2 基于SMOTE 算法和动态BP 神经网络代理模型的可靠性优化策略流程图Fig. 2 Flow chart of reliability optimization strategy based on SMOTE algorithm and dynamic BP neural network surrogate model

具体步骤如下：

1） 建立真实的分析模型，工程中常用有限元模型，确定设计变量以及设计空间。通过最优拉丁超立方设计在设计空间选择初始均匀的样本点，并保存到样本点数据库中。

2） 计算样本点对应的有限元模型的真实响应值。

3） 以样本点数据库中的样本点为训练集输入，以对应的真实响应值为输出，训练得到初始的BP 神经网络模型。

建立BP 神经网络模型时，训练集样本越多，所建立的网络模型越接近真实有限元模型，但是调用有限元模型计算的次数也越多。在工程应用中，往往关心的是可靠性优化问题的全局最优解，因此建立BP 神经网络模型的目的是得到全局最优解。本文是通过在每次迭代过程中增加当前最优解周围失效面附近的样本点，来重新构造BP 神经网络模型，经多次迭代后，可以提高代理模型在真实有限元模型可靠性优化最优解附近的近似精度，并在每一次迭代中使用全局优化算法-ASA，来求解代理模型的可靠性优化最优解，直至前后两次所得最优解对应目标函数的相对误差满足收敛条件，便停止迭代。本文提出的动态BP 神经网络方法并不关心代理模型在全局的近似精度，而只关心全局最优解附近的精度，因此可以减少调用有限元模型计算的次数，提高计算效率。

2 数学算例及结果分析

2.1 数学模型及优化结果

2.1.1 数学算例1

为了证明本文所提的基于SMOTE 算法和动态BP 神经网络模型的可靠性优化方法的有效性，引用文献[5] 中具有非线性失效面的数学算例进行了测试。

算例的可靠性优化数学模型如式（3）所示。

分别对使用本文动态BP 神经网络模型和文献[11]中序列代理（SSRBO）模型以及静态BP 神经网络模型计算的结果进行了对比，3 种方法的优化结果和计算分析模型的次数如表1所示。

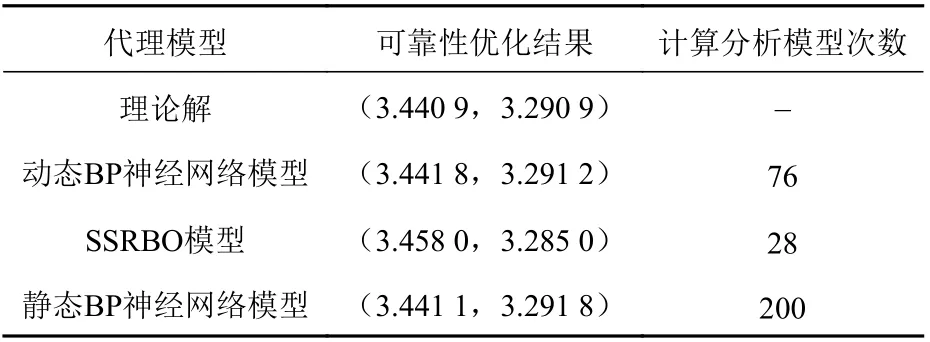
表1 动态、静态BP 神经网络及SSRBO 方法可靠性优化结果对比Table 1 Reliability optimization results comparison of dynamic，static BP nueral network and SSRBO

由表1 可知，采用本文提出的动态BP 神经网络模型和传统的静态BP 神经网络模型均可求解得到该数学问题的可靠性优化全局理论最优解。但从优化效率上看，采用本文提出的动态BP 神经网络模型计算分析模型的次数为76 次，相比传统的静态BP 神经网络模型，计算分析模型的次数减少了62%。由此可见，使用本文提出的基于SMOTE 算法和动态BP 神经网络模型的可靠性优化方法不仅可以获得全局最优解，还显著减少了计算分析模型的次数，提高了可靠性优化效率。

从计算分析模型次数上看，虽然本文提出的动态BP 神经网络模型比SSRBO 模型的次数多一些，但二者的计算次数仍属同一数量级。相比传统的求解方法，本文方法已经可以满足工程问题的求解需要，也提供了一种可靠性优化求解新思路。从可靠性优化结果精度上看，本文的动态BP 神经网络模型得到的最优解与理论解的误差仅为0.026%，而SSRBO 模型所得最优解与理论解的误差为0.497%，可见采用本文方法得到的可靠性优化结果的精度相对更高。采用动态BP 神经网络模型和传统的静态BP 神经网络模型在各自得到的最优解处的代理模型响应值与式（3）中数学表达式的计算模型的真实响应值的对比如表2 所示，最优解处的计算误差如表3所示。

表2 最优解处代理模型与计算模型的响应值对比Table 2 Response values comparison of surrogate model and calculation model at the optimal solution

表3 最优解处计算结果误差对比Table 3 Error comparison of calcuation results at the optimal solution

由表3 可以看出，在最优解附近，本文提出的动态BP 神经网络模型的近似精度要优于静态BP神经网络模型，并且可以很好地近似真实计算模型。这是因为动态BP 神经网络模型将样本点主要分布在最优解附近，提高了BP 神经网络模型在全局最优解附近的近似精度，所以通过SLA 和ASA 进行可靠性优化求解可以获得真实计算模型的全局最优解。

2.1.2 数学算例2

采用文献[12]中具有强非线性的数学算例进行测试，算例的可靠性优化数学模型如式（4）所示。

将使用本文动态BP 神经网络模型和文献[11]中的自适应混沌单循环方法（AK-ACSLA）计算的结果进行了对比，2 种方法的优化结果及计算分析模型的次数如表4 所示。

表4 动态BP 神经网络模型与自适应混沌单循环方法的可靠性优化结果对比Table 4 Reliability optimization results comparison of dynamic BP nueral network model and AK-ACSLA

由表4 所示计算分析模型次数上看，虽然本文提出的动态BP 神经网络模型的计算分析模型次数比AK-ACSLA 法的多，但二者的计算次数还是属于同一数量级，相比传统的求解方法，本文方法已经可以满足工程问题的求解需要，具有一定的精度，也提供了一种可靠性优化求解新思路。

2.2 参数选取讨论

为了探讨本文所提的基于SMOTE 算法和动态代理模型的可靠性优化方法中参数m（选取的少数样本点数量）和参数N（每次迭代产生的新样本点倍数）的选取原则，针对数学算例1，选取表5所示的几组参数进行了对比。

由表5 可知：

1） 本算例中，m 取3 或4 时得到最优解所需的总样本点数量较少；

2） N 较小时虽然每次增加的样本点数量少，但是迭代收敛所需的次数多，因此所需的总样本点数量也较多，而当N 较大时则相反；

3） 参数m 和N 取不同的值对于最终求解得到的最优值影响不大。

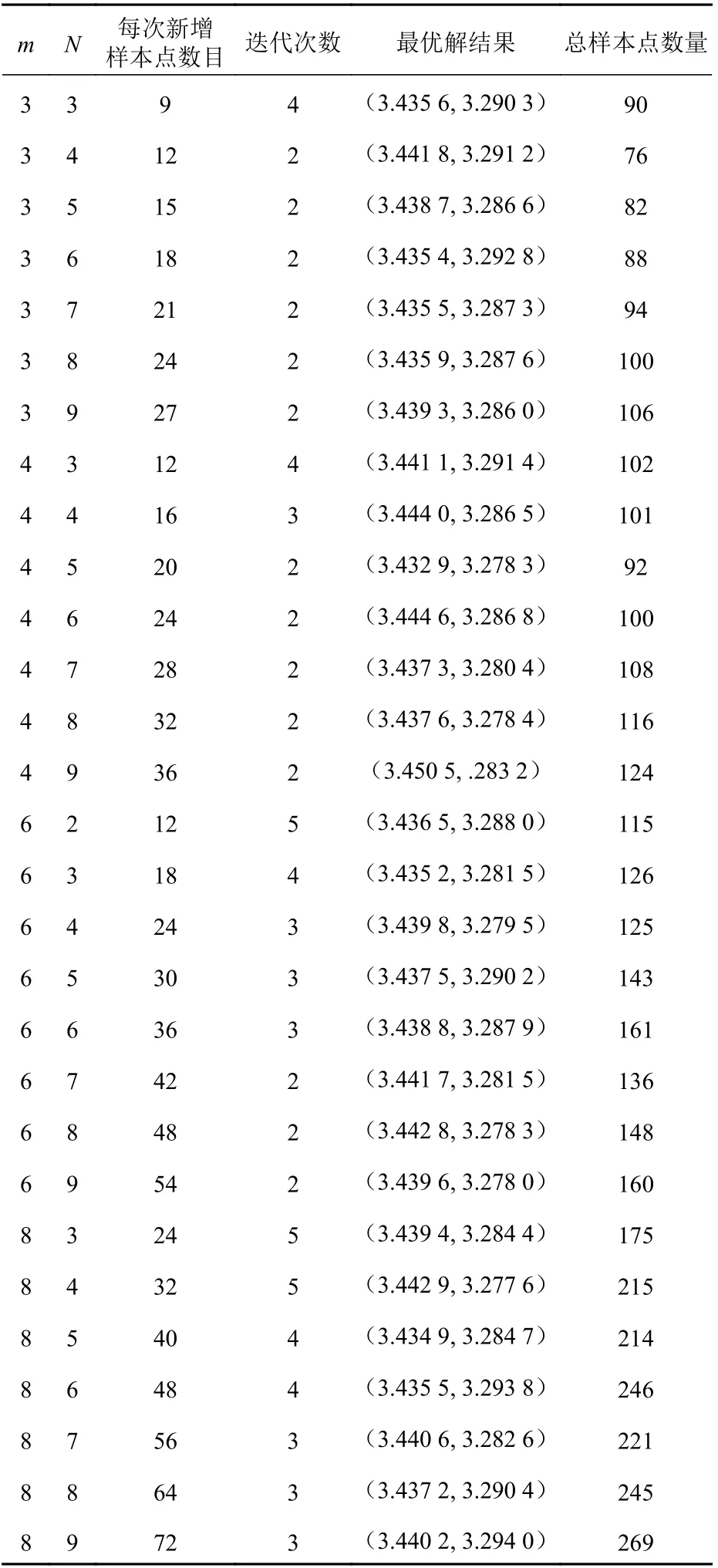
表5 参数m 和N 选取结果对比Table 5 Optimization results comparison of different parameter m and N

这是因为需要从失效面附近选取距离当前最优解最近的m 个样本点，然后使用SMOTE 算法在这m 个样本点中增加N 倍数量的新样本点。如果m 选取过大，新增样本点的选取范围也将过大，在新增样本点数量一定的情况下，位于最优解附近的样本点数量就会过少，所以代理模型的近似精度就会不够，从而导致迭代次数增多。

综上，对于参数m 和N 的选取，建议m 选择为初始位于失效面附近样本点数量的30%～40%（本算例中，初始位于失效面附近的样本点数量为8），N 可适当大一些（3～5 均可），这有利于提高得到全局最优解的计算效率，减少计算成本。

3 船舶结构可靠性优化实例

3.1 船舶结构可靠性优化模型

本文基于上述SMOTE 算法和动态BP 神经网络模型方法，对一艘618 TEU 型多用途船舶的货舱舱段进行了可靠性优化设计。该船主要用于装载集装箱和矿石等散装货物，主要参数如表6 所示。

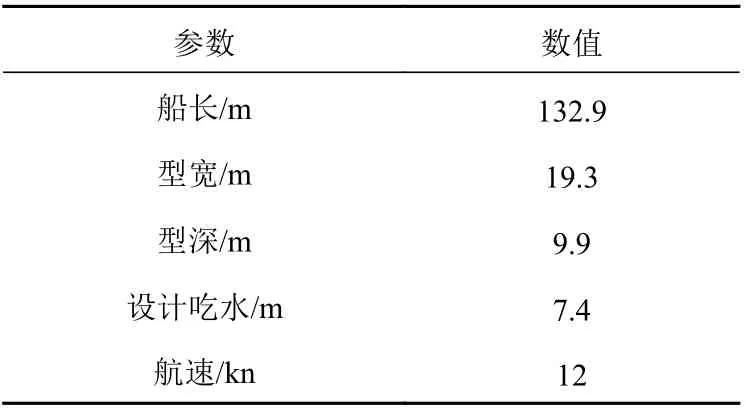
表6 618 TEU 型多用途船舶的主要参数Table 6 Main parameters of 618 TEU multi-purpose ship

此多用途船舶共有3 个货舱舱段，本文建立的可靠性优化模型即为此三舱段模型。舱段所受载荷和约束条件根据中国船级社的《散货船结构强度直接计算指南》确定[19]。计算的工况为：所有货舱满载，最大吃水，所有压载舱均为空舱。

板材尺寸对船体总纵强度和船体总重量影响较大，因此本文选择中剖面的板材厚度作为设计变量。每种板材厚度以其初始厚度为中心，步长为1 mm，取5 个离散值作为设计变量的取值范围，共16 个设计变量，不考虑随机参数的影响。设板材厚度为正态分布的随机变量，其标准差为加工允许偏差，一般取板材厚度均值的2%，即板材厚度设计变量服从分布 N(μxi,0.02μxi)。具体设计变量的分布位置如图3 所示，其中骨材的形状和尺寸视为已知量。

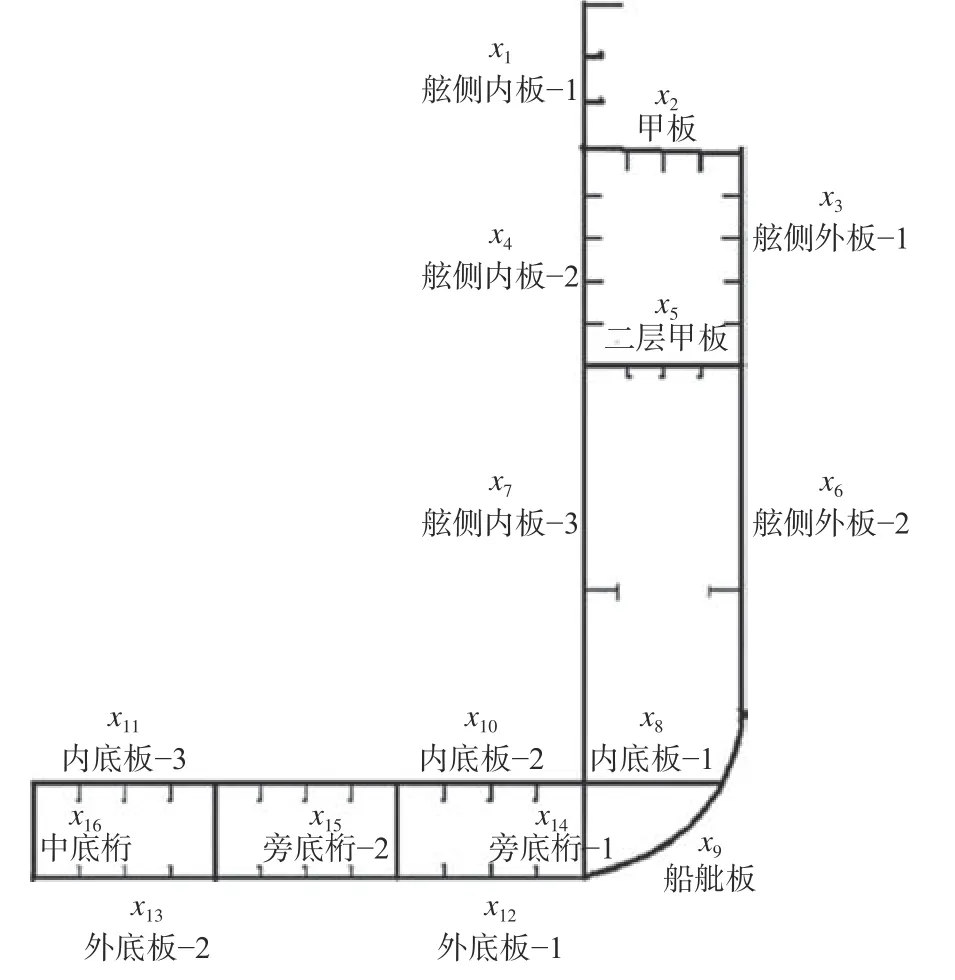
图3 货舱区中剖面图及设计变量分布位置图Fig. 3 Mid-ship section and distribution of design variables

式 中： σi(x) 为第i个 极 限 状态函数； gi(x)为 计 算 所得各区域的应力。 gi(x)对应的计算区域及许用应力值如表7 所示。

表7 gi(x)对应的计算区域及许用应力值Table 7 Analysis domain and allowable stress values for gi(x)

3.2 船舶结构可靠性优化结果

按照1.4 节所述的基于SMOTE 算法和动态BP 神经网络模型的可靠性优化流程，基于Matlab和Isight 平台，对此船舶舱段进行可靠性优化设计，具体过程如下：

1） 采用最优拉丁超立方试验设计在设计空间均匀生成200 个样本点，然后调用有限元模型计算其对应的响应。以该样本点集为训练集输入，以对应的真实响应值为输出，训练得到初始的BP 神经网络模型。

2） 使用SLA 并结合ASA 进行可靠性分析和优化计算，得到当前的可靠性优化最优解。

3） 筛选位于失效面附近的点，调用Matlab 找到最优解附近的10 个样本点，对这些样本点，利用SMOTE 算法扩大3 倍，生成30 个新的样本点，并调用有限元模型计算其对应的响应。

4） 将新增的样本点和计算得到的最优解加入训练集重新训练，更新BP 神经网络模型。

5） 迭代优化，直至相邻两次优化解对应的目标函数值的相对误差小于0.2%，便停止迭代，优化结束。

按照上述方法，使用本文所提的基于SMOTE算法和动态BP 神经网络模型的可靠性优化方法（表8 中的动态BP 神经网络模型），并考虑式（4）的所有约束条件，对此船舶舱段进行可靠性优化。考虑式（4）中的前6 个确定性约束条件，不考虑Pr≥99.653%的可靠性约束条件，进行确定性优化。使用传统的基于一次选点的BP 神经网络模型可靠性优化方法（表8 中的静态BP 神经网络模型），针对上述船舶舱段可靠性优化问题构造BP 神经网络模型并优化。构建BP 神经网络模型时的参数取值保持一致，分别为：最大训练次数Pmax=10 000，学习率η=0.05，训练后网络所需要达到的最小精度 Emin=0.001。3 种方法的优化结果对比如表8 所示。从表中可以看出，本文所提可靠性优化方法在保证得到全局最优解的同时，还显著缩减了计算量。

表8 确定性优化与静态BP 神经网络模型、动态BP 神经网络模型可靠性优化结果对比Table 8 Reliability optimization results comparison of deterministic optimization，static BP neural network model and dynamic BP neural network model

由表8 还可知，使用动态BP 神经网络模型得到的可靠性优化设计结果与初始设计相比质量减少了5.578%，与确定性设计结果相比质量增加了0.874%，这是因为可靠性优化考虑了设计变量的不确定性，牺牲了少部分的目标值来达到可靠性的要求。

采用蒙特卡罗方法对使用动态BP 神经网络模型得到的可靠性优化方案的可靠度进行了验证。在进行可靠性计算时，考虑板材厚度正态分布，将具体板材厚度数据作为均值，其标准差取均值的2%进行可靠性计算。为了保证验证结果的可靠性，选取了1 ×106个随机样本点进行计算，得到可靠度 Pr=99.96%，达到了预设要求。将可靠性优化得到的最终方案代入有限元进行计算，得到的目标质量和约束条件对比如表9 所示。由表可知，动态BP 神经网络模型在最优解处具有较高的预测精度。

表9 可靠性优化设计与有限元结果对比Table 9 Comparison of reliability optimization and FE results

4 结 语

本文针对船舶结构优化中设计变量存在不确定性的问题，提出了结合SMOTE 算法的动态BP神经网络模型，通过最优拉丁超立方试验设计在设计空间中选择初始样本点，构造BP 神经网络模型，并利用ASA 和可靠性优化设计的SLA 找到当前全局最优解，然后再通过SMOTE 算法增加最优解周围的样本点，更新代理模型以提高其在全局最优解附近的精度，直至优化迭代收敛。

本文以一个具有解析表达式的数学算例为例，基于动态BP 神经网络模型的可靠性优化计算过程，只计算了76 次便得到了可满足可靠性要求的全局最优解；在多用途船舶舱段可靠性优化设计问题中，优化后的舱段结构质量减少了5.578%，可靠度提升到了99.96%，在提高船舶经济性的同时保证了船舶结构的安全性，证明了本文所述方法的有效性。同时，将可靠性优化计算中调用有限元模型的次数减少到了293 次，相比常规的采用静态BP 神经网络模型，显著减少了计算成本，提高了计算效率。

因此，本文提出的基于SMOTE 算法和动态BP 神经网络模型的可靠性优化设计策略能有效解决复杂结构的可靠性设计优化问题，在保证可靠性优化结果准确性的同时大幅度提高优化效率，可为船舶及其他大型复杂结构的可靠性优化设计提供新的思路。