智能电网状态估计中用于提高数据完整性的超分辨率感知技术

梁高琪，刘国龙，赵俊华,c,*，刘艳丽，顾津锦，孙广中，董朝阳

a School of Science and Engineering, Chinese University of Hong Kong, Shenzhen, Shenzhen 518172, China

b School of Computer Science and Technology, University of Science and Technology of China, Hefei 230027, China

c Shenzhen Institute of Artificial Intelligence and Robotics for Society, Shenzhen 518172, China

d School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China

e School of Electrical Engineering and Telecommunications, University of New South Wales, Sydney, NSW 2052, Australia

1. 引言

智能电网是为全社会各行业持续提供安全、经济的电力供应的重要基础设施。智能电网中的状态估计（state estimation）模块在系统监控（system monitoring and control）中起着至关重要的作用，有助于系统操作员感知系统的运行状态，从而做出准确的控制决策[1]。当前，智能电网的发展对状态估计提出了新的要求：一方面，随着可再生能源和新能源设备（如风力发电、太阳能和电动汽车等）的普及，智能电网将具有更大的不确定性[2]。为了减轻间歇性可再生能源对智能电网的不利影响，系统操作员需要更加频繁地感知系统的运行状态，缩短调度间隔，这就需要高频状态估计的支持。另一方面，随着计算能力的迅速提升，大数据技术正被广泛应用于分析系统测量数据来发现隐藏信息[3]。而状态估计是感知系统运行状态的基本工具，可直接监测电压、电流、有功功率、无功功率等数据，高频的状态估计结果有助于发现更多的隐藏信息，因此有利于提高系统的安全性和运行效率。

然而，高频状态估计面临一些实际的挑战和困难。首先，状态估计基于部署在节点、发电机组、传输线路等成千上万个表计来监控系统状态。在现有的数据采集与监视控制系统（supervisory control and data acquisition, SCADA）中，大多数表计都是多年前部署的，并且以相对较低的频率收集数据，如每隔几分钟的采样频率[4,5]。其次，一些高频采样表计，如同步相量测量单元（phasor measurement unit, PMU），虽然能以比传统表计更高的频率采集数据[6-8]，但是单一的测量值不足以支撑状态估计的运算，因为在任何特定的时间点，状态估计的输入必须为一个测量向量。而PMU又较为昂贵，用PMU取代所有传统表计在经济上不现实[7]。此外，即使所有传统的表计都可以被PMU取代，系统的状态感知能力也会受到通信信道容量的限制，造成PMU采集到的高频数据不能完全传输到控制中心，而需要临时存储在远程位置上[5]，因此，PMU的高频数据不能真正得到有效利用。综上所述，目前由于技术等原因限制，实现高频状态估计仍然是一项艰巨的任务。

此外，由于通信故障或网络攻击[9]，如假数据注入攻击（false data injection attack, FDIA）[10,11]、网络拓扑攻击（cyber topology attack）[12-14]和信息物理攻击（cyber-physical attack）[15,16]等，传统表计和PMU收集的数据都有可能丢失或被篡改。现实世界中的网络攻击事件，如2015年12月的乌克兰大停电事故[17]和2019年3月的委内瑞拉大停电事故[18]，都表明网络攻击可能导致严重的后果。目前，有大量的文献提出检测异常数据的方法。例如，Ashok等[19]通过描述基于SCADA的状态估计与基于负荷预测、机组调度和同步相量数据预测的系统状态之间差异的统计特征来检测异常数据。Esmalifalak等[20]利用基于分布式支持向量机（support vector machine, SVM）的方法来区分异常数据和正常数据。然而，就目前文献而言，检测到异常数据后，关于如何快速修复异常数据的研究非常有限。从这个层面来说，丢失的或被篡改的数据也给状态估计的精准状态感知带来了不小的挑战。

在上述背景下，为了应对这些挑战，基于现有测量条件，需要提出有效的方法来达到系统运行状态的高频感知。本文把这一问题看作一个数据完整性改进问题，认为控制中心接收到的原始测量数据为不完整数据（即低频数据），系统操作员用于高频决策的数据为完整数据（即高频数据）。因此，这一问题相当于解决了如何从低频数据中恢复高频数据以达到提高数据完整性的难题。不同研究领域针对该问题的视角和解决方法可能有所不同，而针对智能电网，探索合适的方法来提高其状态估计的数据完整性至关重要。

本文将采用超分辨率（super resolution, SR）技术来实现这一目标[21,22]。目前，从低分辨率数据中获取高分辨率数据最有效的方法分别是基于插值、重建和机器学习[23]。基于机器学习的SR技术，通过给定的样本获取低分辨率和高分辨率图像块之间的先验映射，具有良好的性能表现，成为近些年的研究热点[24]。例如，Dong等[25]提出了一种新的深度学习方法，即超分辨率卷积神经网络（super-resolution convolutional neural network, SRCNN），用于学习低分辨率和高分辨率图像之间的端到端映射，该方法在恢复高分辨率图像方面表现出优越的性能。Wang等[26]提出了一种增强的超分辨率生成对抗网络（enhanced super-resolution generative adversarial network, ESRGAN）来恢复图像，结果表明，该方法比其他SR方法效果更好。

综上所述，系统运行状态的高频感知对智能电网的发展具有重要意义。然而，传统表计采样频率低、PMU投资成本高、通信信道容量受限、通信错误或网络攻击等，使得状态估计的高频感知在实际应用中存在阻碍和挑战。因此，本文旨在提出一种超分辨率感知（super resolution perception, SRP）的技术来提高智能电网状态估计的数据完整性。本文的主要贡献如下：

（1）本文是最早研究智能电网状态估计数据完整性问题的文献。

（2）本文提出了一种有效的SRP方法，即超分辨率状态估计网络（super resolution perception net for state estimation, SRPNSE），用于从低频数据中恢复高频数据，并应用于状态估计，同时证明了该方法的有效性和实用价值。

本文结构如下：第1节为背景介绍；第2节描述了智能电网状态估计及其数据完整性问题；第3节给出了SRP模型，并给出了SRPNSE的网络结构和基于深度学习的求解方法；第4节通过仿真验证了该方法的有效性；第5节给出结论和未来的研究方向。

2. 状态估计中的数据完整性问题

本节中，我们将对智能电网状态估计与其数据完整性问题做一个简要的介绍。

2.1. 智能电网状态估计

在智能电网中，感知系统运行状态的关键在于获得系统的测量数据，即电网每个节点（bus）的稳态电压（包括相角和幅值）。一旦掌握了电压信息，就可以使用潮流方程[4,5]计算出对应的其他状态变量。但是，并非所有节点的电压幅值和相角都可以被轻易获取，实际中还需要测量一些其他数据，如某些传输线路的有功和无功功率、某些节点的有功和无功注入功率等，以满足不同的控制目的（如为紧急情况提供预警）。此外，需要指出的是，由于干扰或网络攻击可带来测量误差，并非所有测量数据都是可靠的。而状态估计是一种利用上述可用的测量数据以及综合的冗余信息，通过一定方法估计系统状态变量的工具。

通常来说，状态估计是智能电网能源管理系统（energy management system, EMS）中一个至关重要的模块，扮演着在线监视、分析和控制的重要角色。除了必要的通信网络外，与状态估计密切相关的模块主要包括三部分：传感器（sensor）、状态估计器（state estimator）和坏数据检测器（bad data detector）。传感器以一定的采样频率[1]测量系统状态，如电压幅值、有功和无功功率等；状态估计器使用所有收集的数据来估计系统状态变量，以获得稳定状态下的电力系统概貌；坏数据检测器将检测并剔除明显的错误数据。

状态估计过程是一个广义上的潮流计算模型。如下所示，z表示维度为[m, 1]的由所有测量数据组成的向量；x表示维度为[n, 1]的由所有状态变量组成的向量，且m ＞ n；h(x)表示测量值和状态变量之间的关系函数；e为维度为[m, 1]的噪声向量。

状态估计的目的是从向量z估计出一个向量x^，使其尽可能接近于真实的向量x。常用的是极大似然（maximum likelihood, ML）估计法：

式中，p(z)是z的概率分布密度函数。

不同的向量z的分布假设，可对应不同的估计器，如加权最小二乘估计（weighted least square, WLS）、加权最小绝对值估计（weighted minimum absolute value,WLAV）、最小平方中值估计（least median of square,LMS）、最小截断平方估计（least trimmed square, LTS）和非二次估计（non-quadratic estimator）等[5]。一般地，若测量噪声遵循正态分布，则WLS将是最优选择。需找到目标函数J(x)的极值：

式中，R是测量误差方差的对角矩阵。

2.2. 状态估计的数据完整性

数据质量在任何工业问题中都是关键因素，没有高质量的数据，解析模型和数据驱动模型的表现都会受到严重影响。当使用劣质数据时，模型结果会遇到不可预测的偏差，进而带来重大经济损失和安全风险。就现有文献来看，大多数数据质量研究都集中于数据库系统领域[27]。而数据完整性是评估数据集质量的重要指标[27]，通常被定义为实际收集的数据和预期收集的数据之间的差距，即是否存在丢失的数据、损坏的数据或被篡改的数据[28]。

本文认为，控制中心收集到的低频率测量数据是不完整的，而高频时间序列是期望收集到的数据，是完整的。以离散序列zk(·)代表向量z的第k行数据[即zk(·)代表了第k个表计的测量值]，其对应的数学表达式为：

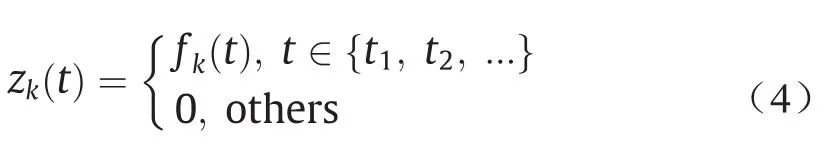
式中，fk(t)代表第k个表计在时间t的测量值的函数。

由于传统表计的采样频率低、通信信道的容量限制、通信错误甚至网络攻击等因素，zk(t)的部分数据是缺失的。同样，我们可以定义另外一个时间序列z～k(t)，其时间标注t与zk(t)不同，如公式（5）所示：

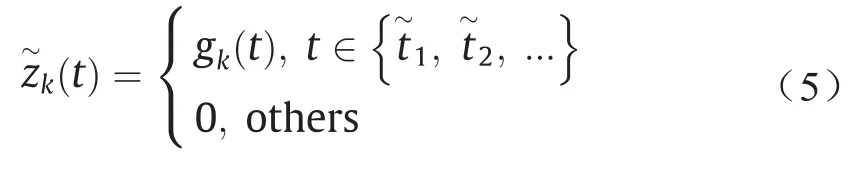
式中，gk(t)代表了第k个表计在时间t的测量数据的函数。

以zk(t)表示上述汇总的时间序列，于是有Zk(t) = zk(t)+ z～

k(t)，如公式（6）所示：例如，当图1（a）、（b）分别为时间序列zk(t)和z～k(t)时，汇总的时间序列如图1（c）所示。

需要指出的是，本文针对状态估计的数据完整性主要是指在时间维度上的测量向量z的完整性，而数据完整性的改进则是指基于可用信息生成更多数据，从而使其尽可能地接近实际值，即恢复丢失的时间序列z～k(t)。

3. SRP模型及其求解方法

在本节中，首先提出了SRP模型及问题；其次，描述了状态估计中数据完整性改进问题；然后，基于深度神经网络强大的特征提取能力，提出了一种深度学习框架，即SRPNSE；最后，介绍了求解SRPNSE模型参数的优化算法。

3.1. SRP模型

忽略系统大小，状态估计的输入是许多表计在特定时间点采集到的测量值形成的向量。在给定向量z的情况下，数据完整性改进问题的目标是恢复每一个表计丢失的数据。我们可以顺序针对该向量对应的各个表计，即恢复每个特定表计的缺失数据相当于一个独立的SRP问题。SRP模型可以表述为：

式中，Lβ为表计实际采集的低频数据；H为原始高频数据；e为噪声向量，由表计导致；↓β为下采样函数，其中β为下采样因子。例如，假设H是以60 Hz采样得到的测量值向量，若β为10，则Lβ是基于H的采样频率为6 Hz的测量值向量。

本文将SRP问题描述为一个最大后验（maximum a posteriori , MAP）估计问题。最大后验估计的目标是估计一个Hβ以最大化后验概率，如式（8）所示：

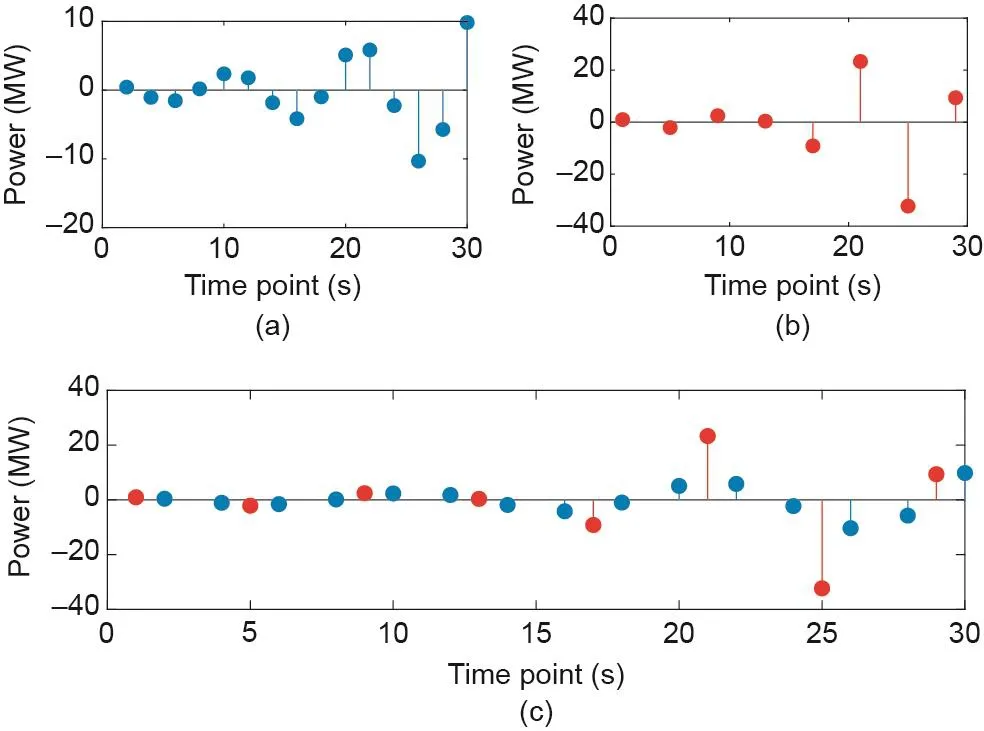
图1. 表计k的离散序列关系。时间序列zk(t)（a）和（b）以及汇总时间序列zk(t)（c）。

式中，p(Lβ, ↓βH)为似然函数；p(↓βH)为↓βH的先验概率。由此可见，先验概率主要与表计的原始采样误差有关。由于状态估计模型假设测量噪声服从正态分布，因此，本文假设先验概率也服从正态分布。

3.2. 问题表述

提高状态估计数据完整性的问题相当于由低频数据生成高频数据的问题。高频数据可以恢复不完整数据中的丢失信息，因此被认为是完整数据。SRP问题如图2所示。给定一组原始数据D，两个下采样数据集Lα和Hβ分别由下采样因子α和β生成。SRP的目标是以低频数据Lα作为输入，生成一组尽可能逼近实际下采样数据Hβ的估计高频数据。ℓ2-norm可用于测量Hβ和之间的差异。

3.3. SRPNSE框架

本文所提出的SRPNSE方法的网络结构如图3所示。SRPNSE网络直接使用低频数据作为输入，然后进行信息增强以输出估计的高频数据。SRPNSE通过以下三个步骤实现数据质量提升：特征提取、信息补全和数据重建。

在特征提取阶段，使用三个一维（1D）卷积层[29]从低频历史数据中提取特征。在获得抽象特征后，第二阶段，即信息补全（information completion）阶段，将基于从低频数据和高频数据之间的内在联系中学习到的信息，提供更高分辨率的特征。信息补全阶段由几个SRPNSE块组成，这些块由残差结构（residual structure）实现。残差结构由一个大的全局残差连接（global residual connection）和若干个局部残差块（local residual block）组成。全局残差连接迫使网络去学习丢失的信息，而不是直接形成信号，而局部残差块提供了训练更深层网络的可能性[29]。为了获得更好的性能，本文在信息补全阶段共使用了22个局部残差块。图4为本文使用的残差块的结构，其中g表示上一层的输出；修正线性单元（rectified linear unit, ReLU）函数[29]为激活函数；identity表示恒等映射。然后，在第三阶段（数据重建），包含更多系统模式细节的高分辨率特征被用于重建目标高频数据，该部分由三个一维卷积层实现。在该部分中，信息补全输出的特征向量被整合成长度为l的子序列β。然后将子序列β重新排列成长度为β×l的重建的高频序列。

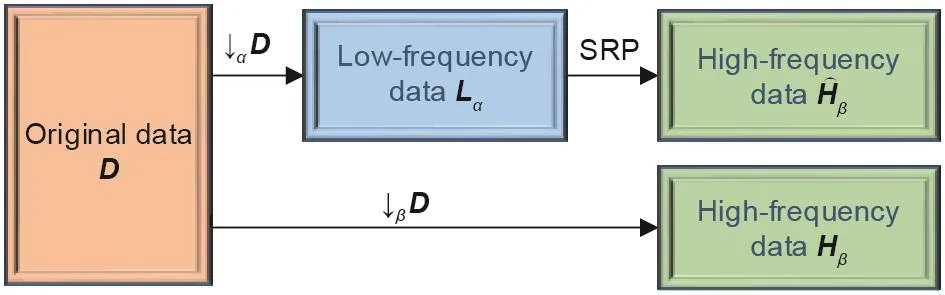
图2. SRP问题示意图。

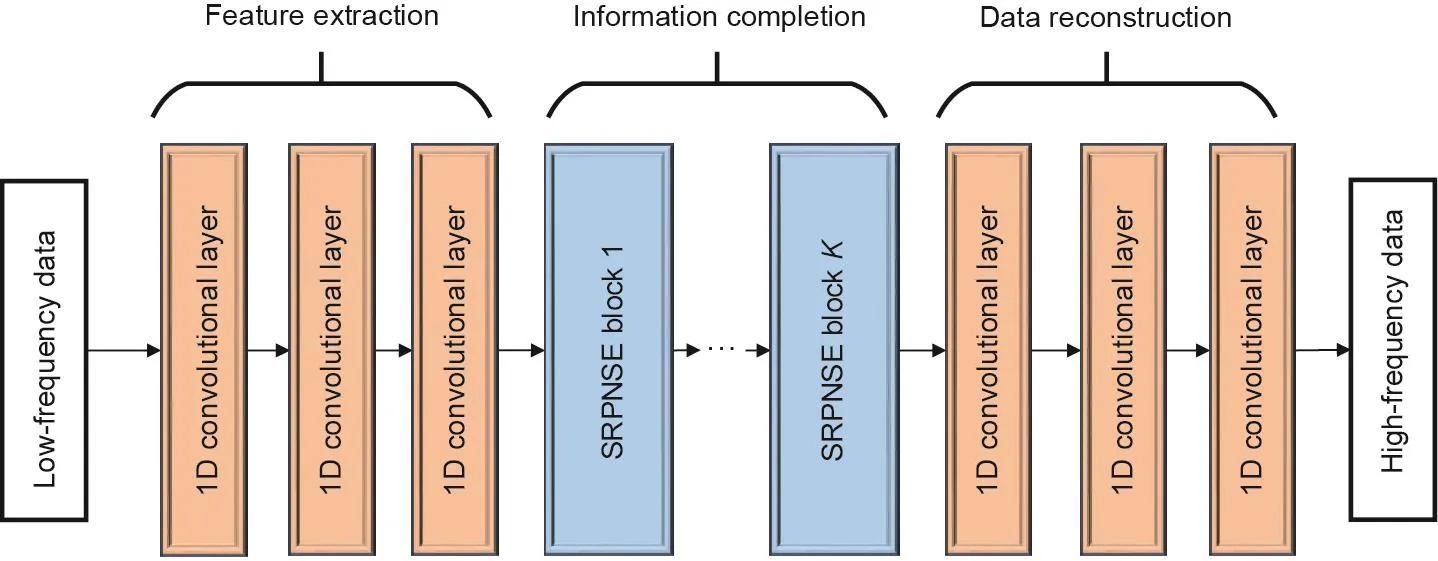
图3. SRPNSE网络结构框架。

在训练本文提出的SRPNSE网络时，选取均方误差（mean squared error, MSE）作为损失函数，如下式所示:

式中，和Hiβ分别是和Hβ的第i项；N是向量大小。

本文以平均绝对百分误差（mean absolute percentage error, MAPE）[30]和信噪比（signal noise ratio, SNR）[31]作为评价指标。MAPE表示与实际值相比的平均绝对误差的程度，MAPE值越高，表示实际值与测试值之间相差越大，其计算方法如式（11）所示：

在信号处理领域，SNR是指信号的平均功率与噪声的平均功率的比值，SNR值越高，说明测试值所包含的噪声越小。其计算方法如式（12）所示，

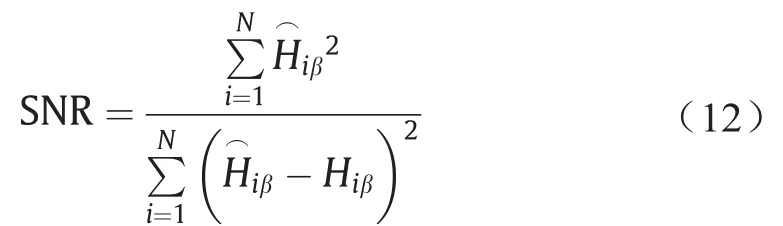
图4. SRPNSE模块i的网络结构，其中i = [1, 2, ..., K]。

3.4. 优化方法

本文提出了一种新的神经网络——SRPNSE，用于解决SRP问题。它是一种由多个残差块组成的深层神经网络，具有很强的表达能力。也就是说，给定一个特定的非线性函数，通过适当调整其参数，神经网络可以渐近逼近该函数。然而，由于网络中存在激活函数和多个隐藏层，SRPNSE的函数具有高度的非线性和非凸性。SRPNSE的非线性和非凸性使得其参数优化变得非常困难。本文研究了估计SRPNSE参数的有效优化算法。

在现有文献中，基于梯度的算法（如算法1所示）仍然是深度神经网络参数估计的主流方法。典型的例子有批量梯度下降（batch gradient descent, BGD）、随机梯度下降（stochastic gradient descent, SGD）和小批量梯度下降（mini-batch gradient descent, Mini-BGD）算法[32]。在这些算法中，参数更新根据以下公式进行：

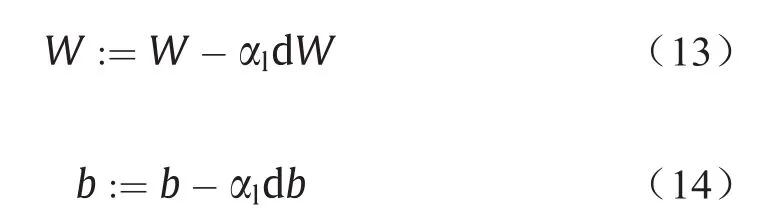
式中，W为权重；b为偏差；α1为学习率；dW和db分别为代价函数相对于变量W和b的偏导数。

算法1. 梯度下降算法的伪代码需要：关于参数θ的目标函数f(θ)需要：学习率α1需要：初始参数θ0 = 0，t = 0若{未收敛}则循环：1. 计算目标函数关于当前参数的梯度：gt = ∇f(θt)2. 计算当前的下降梯度：η = -αlgt 3. 根据下降梯度更新参数：θt+1 = θt + ηt t = t + 1结束返回θt+1

这些基于梯度的算法的主要区别在于，当在一次迭代中更新参数时，BGD基于所有批次的训练数据对网络进行训练，SGD只随机选择一批数据进行训练，而Mini-BGD则选择一部分批次数据。BGD算法最大的缺点是收敛速度慢，尤其是在批次数量较大的情况下，因为它通过计算所有批次来求解梯度。此外，由于SGD和Mini-BGD的梯度方向更新依赖于一个或几个数据批次，它们的收敛轨迹非常不稳定，会导致连续振荡和陷于局部最优。鉴于传统方法的不足，基于等式（13）、（14），许多其他的方法，如动量（Momentum）[32]、自适应梯度算法（adaptive gradient algorithm, Adagrad）[32]、均方根反向传播算法（root mean square prop, RMSProp）[32,33]和自适应矩估计（adaptive moment estimation,ADAM）[32,34]被提出以改进训练过程。在本文，我们研究了两种新算法——RMSProp和ADAM，用于估计SRPNSE参数的有效性。

3.4.1. 均方根反向传播法

优势梯度下降法（dominant gradient descent methods）的一个主要缺点是学习率为固定值，而选择一个合适的学习率是很困难的。如果学习率太小，收敛速度会很慢；如果太大，损失函数会振荡，甚至严重偏离最小值。RMSProp（如算法2所示）是克服这一缺点的优势梯度下降法的一种变体。与等式（13）、（14）比较，RMSProp通过在相邻的小批次上添加平方梯度的移动平均值来实现对学习率的极佳适应[34]。对于每个迭代，如等式（17）、（18）所示，给定的学习率由均方根α1动态调整。均方根实际上是过去梯度平方的指数移动平均值的根。根据等式（15）、（16），RMSProp将更新的依赖性限制在过去的几个梯度上[34]。RMSProp中的均方根是为了平衡不同维的振荡幅度。当参数空间相对平坦时，偏导数较小，指数滑动平均值较小，学习速度加快；当参数空间相对陡峭时，偏导数较大，指数滑动平均值较大，学习速度减慢。

算法2. RMSProp算法的伪代码需要：关于参数W、b的目标函数f(W, b)需要：学习率α1需要：梯度平方的指数衰减平均参数β2需要：初始参数值W0、b0、S0(dW)、S0(db)对于每次迭代t，若{未收敛}则循环：1. 计算目标函数关于当前参数的梯度：dW, db = ∇f(W, b)2. 根据历史梯度计算有偏二阶矩估计值：SdW := β2SdW + (1-β2)(dW)2，Sdb := β2Sdb + (1-β2)(db)2 3. 计算当前的下降梯度：η α ε=- +dW db W l S，η α ε b l=dW- S+db 4. 根据下降梯度更新参数：W := W + ηW，b := b + ηb结束返回W、b

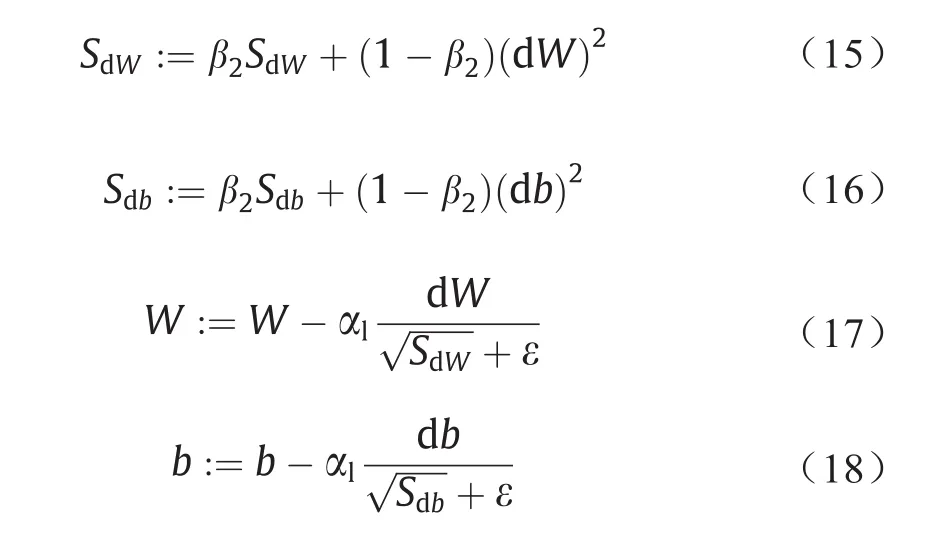
式中，(dW)2和(db)2为梯度的平方；β2为指数衰减率，通常设置为0.9或0.999；SdW和Sdb表示过去梯度平方的指数移动平均值；ε为一个非常小的数，如10-8，以防止分母为0。

3.4.2. 自适应矩估计

优势梯度下降法的另一个缺点是当前的梯度是决定下降方向的唯一因素。一旦当前梯度指向与先前梯度相反的方向，损失函数将振荡甚至偏离最小值。Momentum [32]是克服这一缺点的优势梯度下降法的变体。与等式（13）、（14）比较，Momentum通过累积过去梯度的指数移动平均值，然后向该方向移动，从而实现稳定的更快学习（faster learning）[32]。

ADAM算法（如算法3所示）结合了Momentum和RMSProp算法的思想。梯度的指数衰减平均值，即Momentum由等式（19）、（20）计算得到，在ADAM中被称为“一阶矩估计”；如等式（21）、（22）所示，平方梯度的指数衰减平均值，即RMSProp由等式（21）、（22）计算得到，在ADAM中被称为“二阶矩估计”。此外，如等式（23）、（24）所示，ADAM计算偏置校正后的“一阶矩估计”和“二阶矩估计”，以此来抵消初始化零向量引起的偏差。如等式（25）、（26）所示，ADAM不仅通过梯度的指数衰减平均值更新下降方向，而且还将学习率除以梯度平方的指数衰减平均值。结果表明，该算法收敛速度更快，振荡更小[34]。

算法3. ADAM算法的伪代码需要：关于参数W、b的目标函数f(W, b)需要：学习率α1需要：梯度平方的指数衰减平均参数β1、β2需要：初始参数W0、b0、S0(dW)、S0(db)、v0(dW)、v0(db)对于每次迭代t，若{未收敛}则循环：1. 计算目标函数关于当前参数的梯度：dW, db = ∇f(W, b)2. 根据历史梯度计算有偏一阶及二阶矩估计值：υdW := β1υdW + (1-β1)(dW)2，υdb := β1υdb + (1-β1)(db)2 SdW := β2SdW + (1-β2)(dW)2，Sdb := β2Sdb + (1-β2)(db)2 3. 计算无偏一阶及二阶矩估计值：υ υ c =-:1 dW c db S β、υ υ:1=-、c =-:1 SdW S β、c =-:1 Sdb dW tβdb dW t db t 1 tβ122 4. 根据下降梯度更新参数：W W S:= - +α ε υc W υd d c d W，b : =b -α c b l l c b Sd +ε结束返回W、b

式中，β1表示Momentum的指数衰减率，通常设置为0.9；偏差校正估计值；的当前时间步t的幂。

4. 算例

本节基于一个9节点系统进行算例研究[35]。如图5所示，在节点5、7和9上部署了三个表计以记录负荷的有功功率；在节点1、2和3上部署了三个表计，以测量发电机的有功和无功功率；在线路1～4、5～6、6～7、8～2和9～4的起始位置（如线路1～4的起始位置是靠近1节点处）部署了五个表计，以测量线路有功和无功功率；在线路4～5、3～6、7～8和8～9的终点位置（如线路4～5的终点位置靠近节点5）部署了四个表计，以测量线路有功和无功功率。

为了更好地模拟状态估计时的真实场景，本文假设状态估计的输入值为基于所测负荷的最优潮流（OPF）计算结果的一部分。如图5所示，将记录负荷有功功率的三只表计的数据视为OPF的输入值；将OPF的输出结果（即图5中剩余12只表计包含有功和无功功率，共计24组）作为系统状态估计的输入数据。

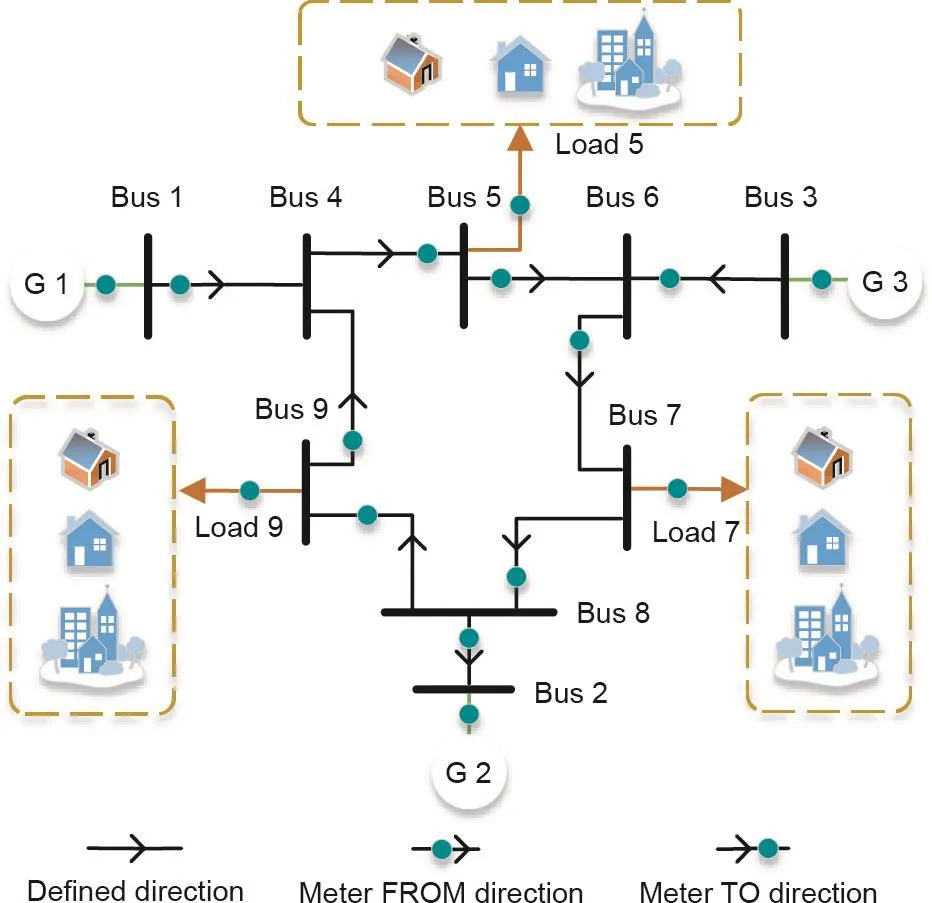
图5. 9节点系统的拓扑结构。G：发电机。

本文假设每个负荷节点基本遵循1 MW的电力大约供给200户家庭的原则。假设每个家庭包含11类家用电器，如空调、加热器、洗衣机、微波炉等。设备的波形均来自公开的设备级负荷识别数据集（plug-level appliance identification dataset, PLAID）[36]，PLAID以3×104Hz的频率采样了11类不同类型的设备，本文将其下采到100 Hz。算例分别模拟了900（节点5）、1000（节点7）和1250（节点9）个家庭，然后分别将对应负荷放大100倍。基于此，形成了本文的超分辨率感知状态估计数据集（super resolution perception state estimation dataset，SRPSED），其发布网址为： https://www.zhaojunhua.org/SRP/SRPSE/dataset/。此外，在生成该数据集时，假设每个家庭都采用普通上班族的用户行为，并且具体用户行为也随数据集一起发布于以上网址。SRPSED总共包含60天的100 Hz频率的高频数据，其中前45天的数据被用于训练和验证，后15天的数据被用于测试。由于本文中的每个表计的数据完整性改进问题是互相独立的，因此我们所提的SRPNSE方法可以以类似的形式被应用于更大的系统。

如表1所示，本文一共进行了4类共16种不同情况的算例研究。其中，f(Lα)和f(H︵β)代表了以Hz为单位的采样频率，且f(H︵β) =ηf(Lα)，η为超分辨率因子（SR factor）。下采样标准基于间隔值而非平均值。算例基于PyTorch 0.4.1，并在具有四个GTX-1080Ti、一个16核CPU和64 GB RAM的GPU集群上实现。

4.1. SRPNSE方法在状态估计中的表现

插值法[37]是一种填补空缺或替换异常数据的常见方式，本文将线性插值（linear interpolation）和立方插值（cubic interpolation）同所提的SRPNSE方法做性能比较。在本文的9节点系统中，状态估计基于给定的测量数据计算系统的状态值，即电压的幅值和相角。并且，状态估计会分别基于真实的下采数据、SRPNSE数据、线性插值数据、立方插值数据进行运算。如表1所示，本文将计算每一个算例的电压幅值和相角的MAPE和SNR值，以此对比不同恢复数据方法的性能优劣。

4.1.1. MAPE指标对比

Appendix A中的Table S1和S2分别显示了基于SRPNSE、线性插值和立方插值情况下的电压幅值和相角的MAPE值；图6和图7分别给出了对应的对比图。需要指出，图6和图7中每个子图都包含四种数据恢复情况。例如，图6（a）表示分别从1/60、1/300、1/600和1/900 Hz往上恢复五倍数据的算例。

4.1.2. SNR指标对比

Appendix A中的Table S3和S4分别显示了基于SRPNSE、线性插值和立方插值情况下的电压幅值和相角的SNR值；图8和9分别给出了对应的对比图。

4.2. SRPNSE方法在负荷节点上的表现

4.2.1. MAPE指标对比

Appendix A中的Table S5、S6和S7分别显示了负荷5、7和9节点上基于SRPNSE、线性插值和立方插值情况下的MAPE值。本文以节点5的情况为代表，如图10所示。

4.2.2. SNR指标对比

Appendix A中的Table S8、S9和S10分别显示了负荷5、7和9节点上基于SRPNSE、线性插值和立方插值情况下的SNR值。本文以节点5的情况为代表，如图11所示。

4.3. 状态估计的可视化比较

本文中的9节点系统共有3台发电机、9个节点和9条线路。文中有4类共16种算例，本文中，我们随机选择算例4、节点3和线路5～6作为代表，以详细显示状态估计的可视化比较。具体来说，我们随机选择一个时间段，依次展示节点3上的电压幅值和相角、线路5～6上的有功功率以及节点3上的发电机出力的波动在η= 5、η= 10、η= 50和η= 100四种情况下的数据恢复结果。在每个图中，我们将真实的下采数据、SRPNSE数据、线性插值数据、立方插值数据进行可视化处理以进行比较。

表1 下采样因子及超分辨率因子

图6. SRPNSE、线性插值和立方插值的电压幅值的MAPE对比。（a）η= 5；（b）η = 10；（c）η = 50；（d）η = 100。

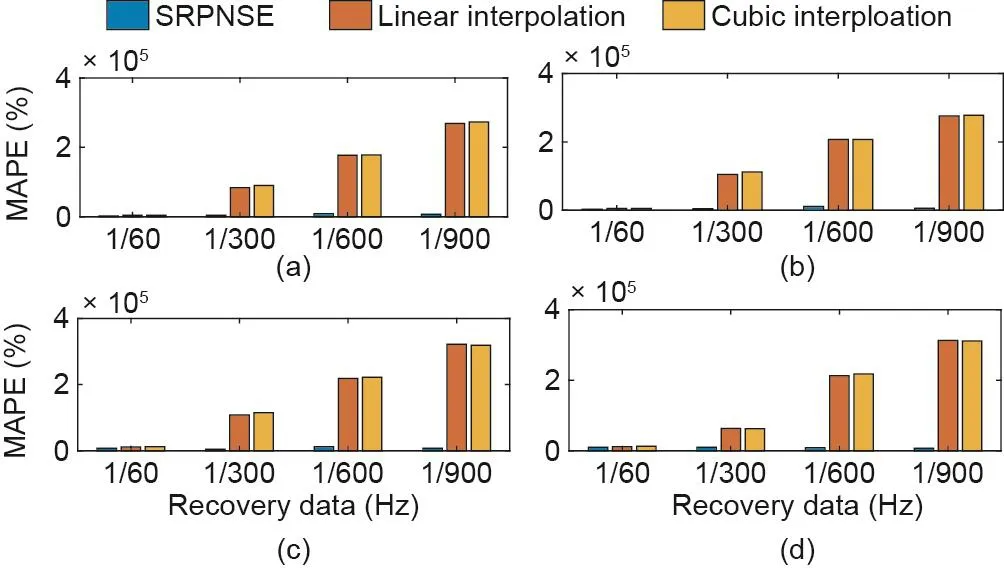
图7. SRPNSE、线性插值和立方插值的电压相角的MAPE对比。（a）η= 5；（b）η = 10；（c）η = 50；（d）η = 100。

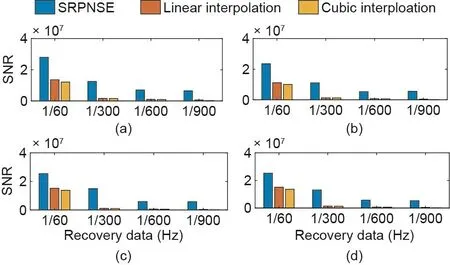
图8. SRPNSE、线性插值和立方插值的电压幅值的SNR对比。（a）η =5；（b）η = 10；（c）η = 50；（d）η = 100。

4.3.1. 算例4且η= 5：节点3的电压幅值

图9. SRPNSE、线性插值和立方插值的电压相角的SNR对比。（a）η =5；（b）η = 10；（c）η = 50；（d）η = 100。

图10. 负荷节点5上SRPNSE、线性插值和立方插值的MAPE对比。（a）η = 5；（b）η = 10；（c）η = 50；（d）η = 100。

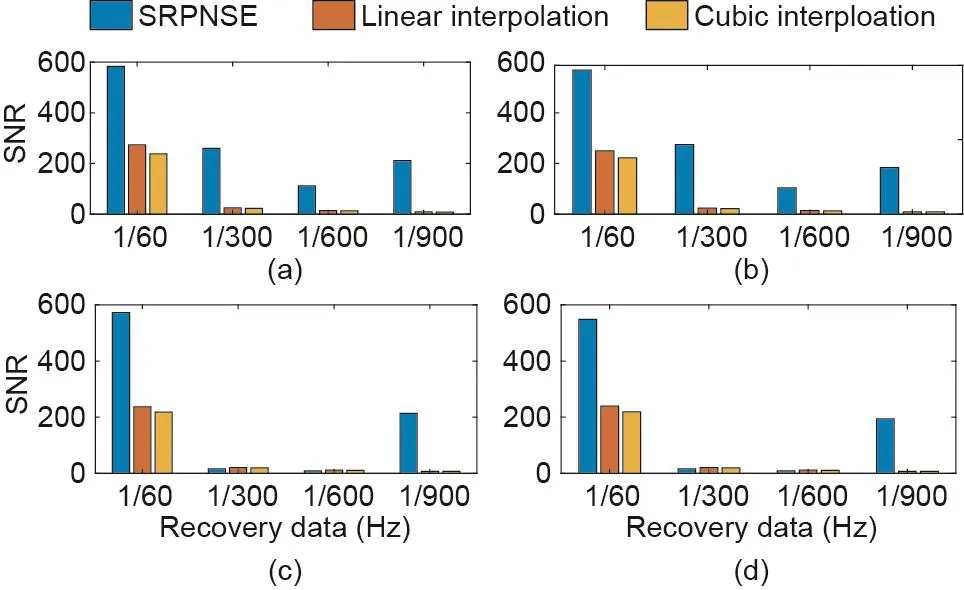
图11. 负荷节点5上SRPNSE、线性插值和立方插值的SNR对比。（a）η = 5；（b）η = 10；（c）η = 50；（d）η = 100。

在这种情况下，α= 90 000、η= 5，即控制中心接收到的低频数据的频率为1/900 Hz，需要从1/900 Hz的数据中恢复出1/180 Hz的数据，随后基于恢复的数据进行状态估计运算。如图12所示，随机选取一段节点3上的电压幅值，分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

4.3.2. 算例4且η= 10：节点3的电压相角

在这种情况下，α= 90 000、η= 10，即控制中心接收到的低频数据的频率为1/900 Hz，需要从1/900 Hz的数据中恢复出1/180 Hz的数据，随后基于恢复的数据进行状态估计运算。如图13所示，随机选取一段节点3上的电压相角，分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

4.3.3. 算例4且η= 50：线路5～6的有功功率

在这种情况下，α= 90 000、η= 50，即控制中心接收到的低频数据的频率为1/900 Hz，需要从1/900 Hz的数据中恢复出1/180 Hz的数据，随后基于恢复的数据进行状态估计运算。如图14所示，随机选取一段线路5～6上的有功功率，分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

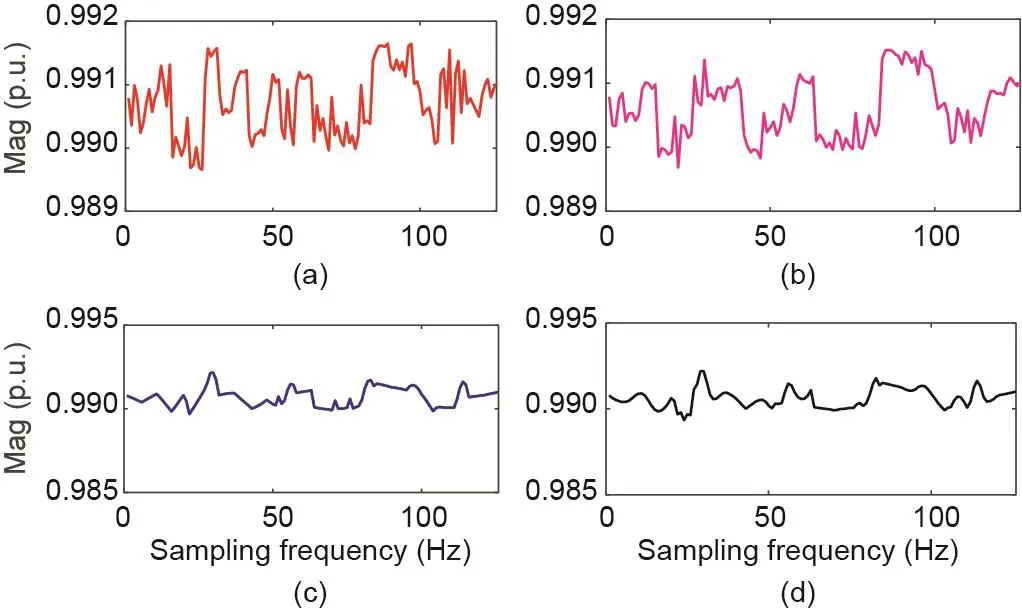
图12. 状态估计运算后，节点3上的电压幅值从1/900 Hz恢复至1/180 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。p.u.：标幺值。

图13. 状态估计运算后，节点3上的电压相角从1/900 Hz恢复至1/180 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

4.3.4. 算例4且η= 100：节点3上的发电机出力

在这种情况下，α= 90 000、η= 100，即控制中心接收到的低频数据的频率为1/900 Hz，需要从1/900 Hz的数据中恢复出1/180 Hz的数据，随后基于恢复的数据进行状态估计运算。如图15所示，随机选取一段节点3上的发电机出力，分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

4.4. 负荷节点的可视化比较

本文共计4类16种不同情况的算例，本文随机选取负荷节点5上的算例1和负荷节点9上的算例4算例，详细讨论恢复的负荷数据情况，并分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

4.4.1. 负荷节点5：从1/60 Hz恢复数据

图14. 状态估计运算后，线路5～6上的有功功率从1/900 Hz恢复至1/180 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

图15. 状态估计运算后，节点3上发电机出力从1/900 Hz恢复至1/180 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

在这种情况下，α= 6000、η= 5、η= 10、η= 50、η= 100，即控制中心接收到的低频数据的频率为1/60 Hz，需要从1/60 Hz的数据中分别恢复出1/12 Hz、1/6 Hz、5/6 Hz、5/3 Hz的数据。如图16至图19所示，随机选择了一个时间段的数据，分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

4.4.2. 负荷节点9：从1/900 Hz恢复数据

图16. 负荷数据从1/60 Hz恢复至1/12 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

在 这 种 情 况 下，α= 9000、η= 5、η= 10、η=50、η= 100，即控制中心接收到的低频数据的频率为1/900 Hz，需要从1/900 Hz的数据中分别恢复出1/180 Hz、1/90 Hz、1/18 Hz、1/9 Hz的数据。如图20至图23所示，随机选择了一个时间段的数据，分别对比了实际下采数据、基于SRPNSE恢复的数据、基于线性插值恢复的数据和基于立方插值恢复的数据。

4.5. 基于SGD、RMSProp和ADAM算法求解SRPNSE的对比

Appendix A中的Table S11和S12分别给出了使用SGD、ADAM和RMSProp算法求解所提出的SRPNSE的MAPE和SNR值的对比情况。本文以这三种算法在负荷节点5上的MAPE值为代表，见图24。

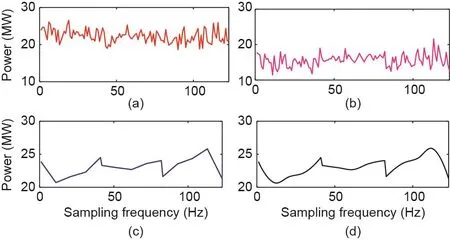
图17. 负荷数据从1/60 Hz 恢复至1/6 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

图18. 负荷数据从1/60 Hz 恢复至5/6 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

图19. 负荷数据从1/60 Hz 恢复至5/3 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

图20. 负荷数据从1/900 Hz恢复至1/180 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

图21. 负荷数据从1/900 Hz恢复至1/90 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

此外，对比了SGD、RMSProp和ADAM算法在每次迭代过程中的损失函数。本文随机选取了算例4且η=100的算例作为代表[图25（a）]。图25（b）分别给出了前80次迭代和300～380次迭代的放大视图。

4.6. 结果分析

Appendix A中的Tables S1～S4、图6至图9和图12至图15给出了对于状态估计结果的比较；Tables S5～S10、图10至图11和图16至图23给出了基于负荷节点数据的比较。需要指出的是，后者是表计测量值的SR结果的对比，而前者则是基于表计测量值SR结果的状态估计运算的对比。

图22. 负荷数据从1/900 Hz恢复至1/18 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

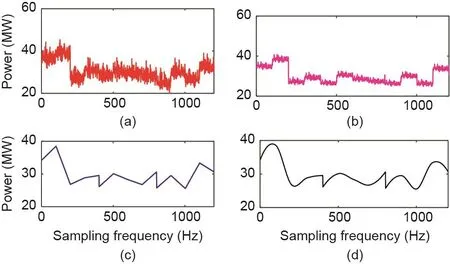
图23. 负荷数据从1/900 Hz恢复至1/9 Hz的情况。（a）实际下采数据；（b）SRPNSE；（c）线性插值；（d）立方插值。

图24. 基于SGD、RMSProp和ADAM算法的MAPE值对比情况。（a）η = 5；（b）η = 10；（c）η = 50；（d）η = 100。

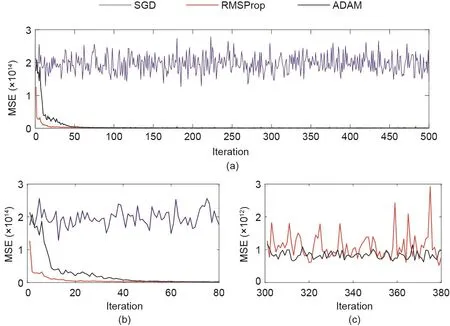
图25. 以算例4且η = 100的算例作为代表，基于SGD、RMSProp和ADAM算法的损失函数对比情况。迭代[1, 500]（a）、迭代[1, 80]（b）及迭代[300,380]（c）中的MSE值。

首先，从Tables S1～S4和Tables S5～S10可以清楚地看出，本文所提出的SRPNSE方法的表现明显优于线性插值法和立方插值法。这表明，通过SRPNSE方法恢复的数据可以实现对实际情况的更准确估计，从而有助于获得更准确的状态估计结果。值得一提的是，SRPNSE、线性插值和立方插值方法之间的对比效果非常显著，如Tables S1～S4和图6至图9所示，相应数据之间的差距可达一至两个数量级。因此，线性插值和立方插值方法在从低频数据中恢复丢失信息方面的能力较弱，而本文所提出的SRPNSE方法表现良好。

其次，从Tables S5～S7可以明显看出，无论超分辨率因子是多少，当采样频率下降时，SRPNSE和插值法的MAPE值都会随之增加，且采样频率越低，SRPNSE和插值法之间的MAPE差异就越大。而在case 1中，SRPNSE和插值方法之间的MAPE差异不大的原因是，采样频率较高的数据已经包含足够的信息，这恰好有助于提高插值的准确性。

再次，通过比较特定情况下不同超分辨率因子的情况，如算例3，η = 5、η = 10、η = 50和η = 100，从Tables S5～S7和Tables S8～S10可以清楚地看出，较小的超分辨率因子通常会使得SRPNSE和插值法都能有较好的表现。

最后，从图24和Tables S11～S12中可以明显看出，基于ADAM算法的MAPE值大多低于基于RMSProp和SGD算法的MAPE值。如图25（a）所示，SGD算法收敛速度较慢，并且持续遇到振荡的情况；如图25（b）所示，与RMSProp相比，ADAM算法的收敛速度稍慢，但其稳定性非常出色。其结果与3.4节的一致，即ADAM算法不仅使用动态调整的学习速率来加快收敛速度，而且使用累积的动量来保持稳定。因此，在解决本文提出的SRPNSE框架方面，ADAM算法的表现要优于RMSProp和SGD算法。

5. 结论

本文提出了一种新的基于机器学习的SRP方法来提高智能电网状态估计的数据完整性，算例证明了该方法的有效性和实用价值。

本文所提的SRPNSE方法是一种在解决状态估计SRP问题时，独立恢复表计高频数据而不使用任何来自相邻表计信息的算法。因此，无论针对多大规模的系统，逐个完成各个表计的数据恢复工作即可。需指出，本文基于一个9节点系统进行算例分析，但是该系统的负荷数据量非常大，约为10 GB。更大的测试系统意味着更大的计算资源，即需要在硬件（GPU和内存）上进行额外投资。我们将此留作日后的工作去完成。未来，我们将在更高频率的数据上进行测试，如从100 Hz、10 Hz或1 Hz起恢复数据。

事实上，SRPNSE方法不仅可以应用于智能电网的状态估计，还可以应用于智能电网中的许多重要模块，甚至其他工业领域。通过应用SRPNSE方法，可以在不需要进一步投资和系统升级的情况下，克服由表计、通信信道和异常数据造成的阻碍和挑战，直接将低质量数据恢复成高质量数据，从而提高现有工业系统的效率和安全性。

致谢

本研究得到了国家自然科学基金重大研究计划（91746118）、深圳市科技创新委员会基础研究项目（JCYJ20170410172224515）、深圳市人工智能与机器人研究院、中国科学院青年创新促进会的支持。

Compliance with ethics guidelines

Gaoqi Liang, Guolong Liu, Junhua Zhao, Yanli Liu,Jinjin Gu, Guangzhong Sun, and Zhaoyang Dong declare that they have no conflict of interest or financial conflicts to disclose.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2020.06.006.