矿用振动筛弹簧永久变形故障研究

郭建华

（山西兰花科创玉溪煤矿有限责任公司，山西 晋城 048000）

关键字：矿用振动筛；弹簧故障；有限元

1 矿用振动筛结构及工作原理介绍

为减少煤炭燃烧带来的环境污染，提高资源的高效利用，筛选煤炭成为行业内的必不可缺的环节[1]，而矿用振动筛设备是选煤的关键工艺装备，具有寿命长、噪声低、筛选效率高等特点，目前广泛应用于对煤炭的筛选分级、脱水、脱泥等工序。

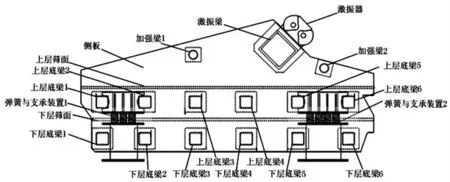
图1 双层矿用振动筛结构示意图

一般而言，洗煤用的大型直线振动筛设备采用的是座式水平安装方式，且具有良好地对称性。此外，矿用振动筛设备的筛面可以采用单层或双层设计方案，如图1所示的某型号矿用直线振动设备则采用的是双层结构设计方案，它的整体结构具有很好的对称性，结构重心位置居中，具有较好的稳定性，下层采用底梁支撑结构，上层采用加强梁进行加强强度设计，上层和下层之间采用弹簧和支承装置进行连接，不仅起到缓冲储能作用，还能以底层作为支撑，起到支承上层的作用。

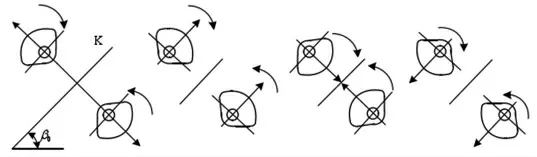
图2 激振器的工作原理图

直线矿用振动筛设备的激振器两偏心块在运转时会产生足够的离心力，两个偏心块同步反向运动，离心力按K方向的分力不断地叠加，但与K方向的垂直方向，其分力不停的相互抵消，故而产生了唯一朝着K方向的激振力，进而驱动振动筛实现直线运动，再加上物料的自身重力，最终形成振动筛在K方向即振动方向做往复直线运动，工作原理如下图所示。从振动筛设备的角度来看，物料从入料端进入，经过上层的运输，较筛孔小的物料透过筛面，落到下一层的筛面，最后被筛后的物料从出料端排出来，其工作原理如图2所示。

2 矿用振动筛有限元分析

在矿用振动筛的实际减震过程中，弹簧在长期的交变载荷作用下可能会发生故障，从而导致整个弹性支撑系统的刚度性能发生变化[2]。根据有限元方法，针对矿用振动筛筛体的主要结构（激振器和弹簧）采用ANSYS软件进行有限元仿真分析，查询机械设计手册[3]和GB/T 713-2014[4]、GB/T 699-2015[5]等 文 献 资料，得到矿用振动筛原材料Q245R钢常温状态的材料参数，再根据矿用振动筛实际工况及其受力情况，对模型进行简化处理，如图3所示，随后进行网格划分，结果如图4所示。

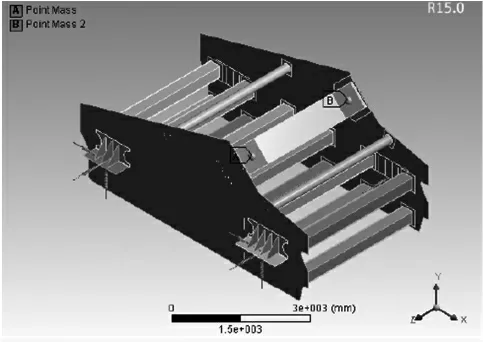
图3 激振器有限元模型图

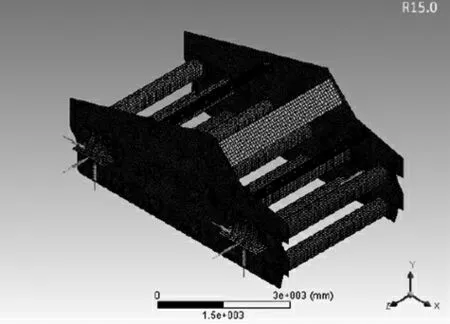
图4 激振器有限元模型的网格划分图

首先，基于静力学分析矿用振动筛激振器在平衡状态下受力的情况。在Static Structural分析中添加重力加速度的参数，得到模型的位移与应力，其结果分别如图5和图6所示，在图片中，黑色线框表示模型结构的初始位置，位移和应力数值最大和最小的节点分别用MAX和MIN进行了标示。矿用振动筛结构本身具有良好的对称性，因而结构的静力学位移、应力也具有对称性特点，最大位移值为28.32mm，位于结构的出料端，而最大应力值为6.345MPa，小于矿用振动筛原材料许用应力，满足设计要求。

其次，采用ANSYS Workbench平台中的Modal分析矿用振动筛固有频率及其振型，判断其在激振力作用下是否会出现共振及不利的振型，并确定结构本身的固有特性参数，从而为模型结构得到较好的使用性能。在实际工况中，虽然矿用振动筛是具有无数个自由度的振动系统，但是对结构使用性能影响较大为结构的低阶固有频率，因此，在有限元模态分析中，只需要明确前面的低阶固有频率及其对应振型，则可确定出矿用振动筛结构的固有特性。采用ANSYS软件中Block Lanczos方法，求解速度快、精度高，对结构的前十一个低阶固有频率及其振型进行模态分析，得到的分析结构如表1所示。

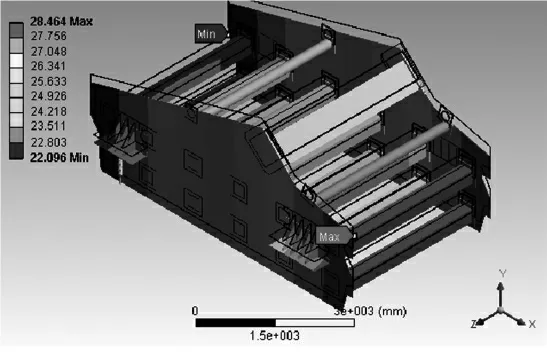
图5 激振器有限元模型结构位移图

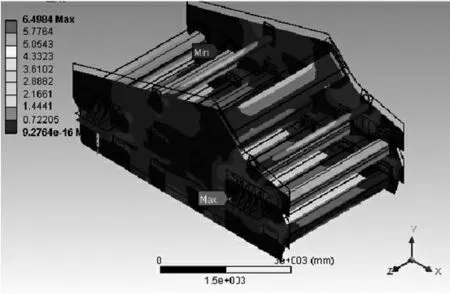
图6 激振器有限元模型结构应力图

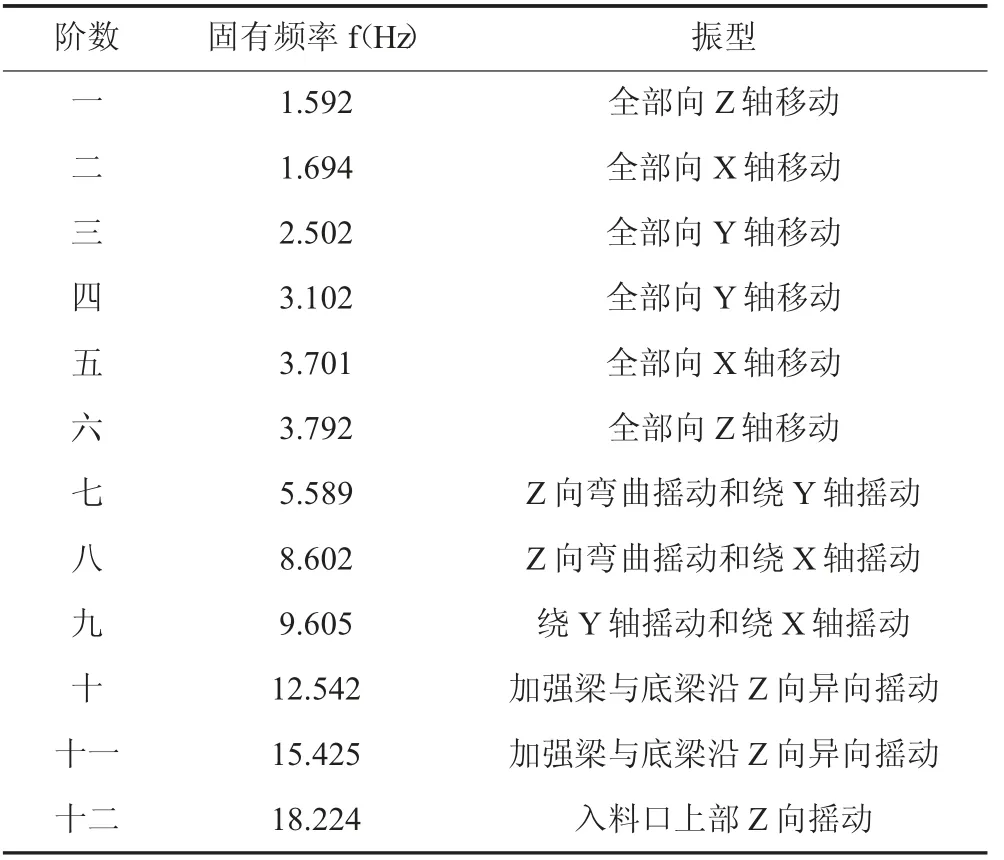
表1 激振器有限元模型模态分析结果

根据分析结果可知，前六个低阶振型均以刚体运动为主，因模型结构的弹性变形较小，固有频率值也较小，其振型包括3个方向的平动和转动，主要为弹簧的变形；从第七至第十二阶的振型主要是以结构的弹性变形为主，振型主要是结构的局部变形；第十一阶的固有频率是15.345Hz，与矿用振动筛设备的工作频率相近，它的振型表现出入料口处的上部分有较大的局部变形，因此在设计过程中应在该处增加加强筋，增强刚度；第十二阶的固有频率为18.224Hz，比矿用振动筛设备的工作频率更大，因此矿用振动筛设备在正常工作状态时，不会出现共振问题。

3 矿用振动筛弹簧永久变形故障试验

文章建立了矿用振动筛的有限元模型，进行了结构静力学分析和模态分析（固有频率及其振型），再以某型号直线振动筛设备为对象，进行振动筛弹簧永久性变形故障动力学试验，以验证理论分析的结果。

3.1 试验介绍

因煤矿厂区为防爆区域，对试验设备有防爆设计要求，所以选用某高校团队研发的YHJ（C）型矿用测振记录仪（含相应的振动传感器）作为试验用仪器装置，完全符合煤矿厂要求[6-7]。针对矿用振动筛的结构特点以及弹簧振动特性，在矿用振动筛的四个弹簧座上分别在三个方向（X轴、Y轴、Z轴）安装加速度传感器，用来检测加速度信号，再换算得到速度和位移信号数据，最终可获得振幅数据，安装的实际效果图如图7所示。

图7 矿用振动筛弹簧传感器安装效果

在试验条件有限的情况下，本次试验采用对比试验方法，在同种工况下，分别采用故障弹簧和非故障弹簧进行单个对比试验，试验过程中人为的降低弹簧性能，故障弹簧刚度比非故障弹簧刚度降低约18%，其余均保证两种弹簧的一致状态。在试验的实施过程中，将矿用振动筛一处的正常弹簧更换为故障弹簧，用以模拟因弹簧永久变形故障而导致的刚度变化，再分别检测得到矿用振动筛在健康工况下的弹簧在三个方向上的振幅数据，得到数据后经换算即可得到振幅变化系数。

3.2 试验分析

经过试验验证，得到检测数据，经换算后得到振幅变化系数，再与前文中的有限元仿真振幅变化数据进行对比，并核算仿真数据与试验数据之间的误差值，最后研究分析振幅变化规律，如表2所示。

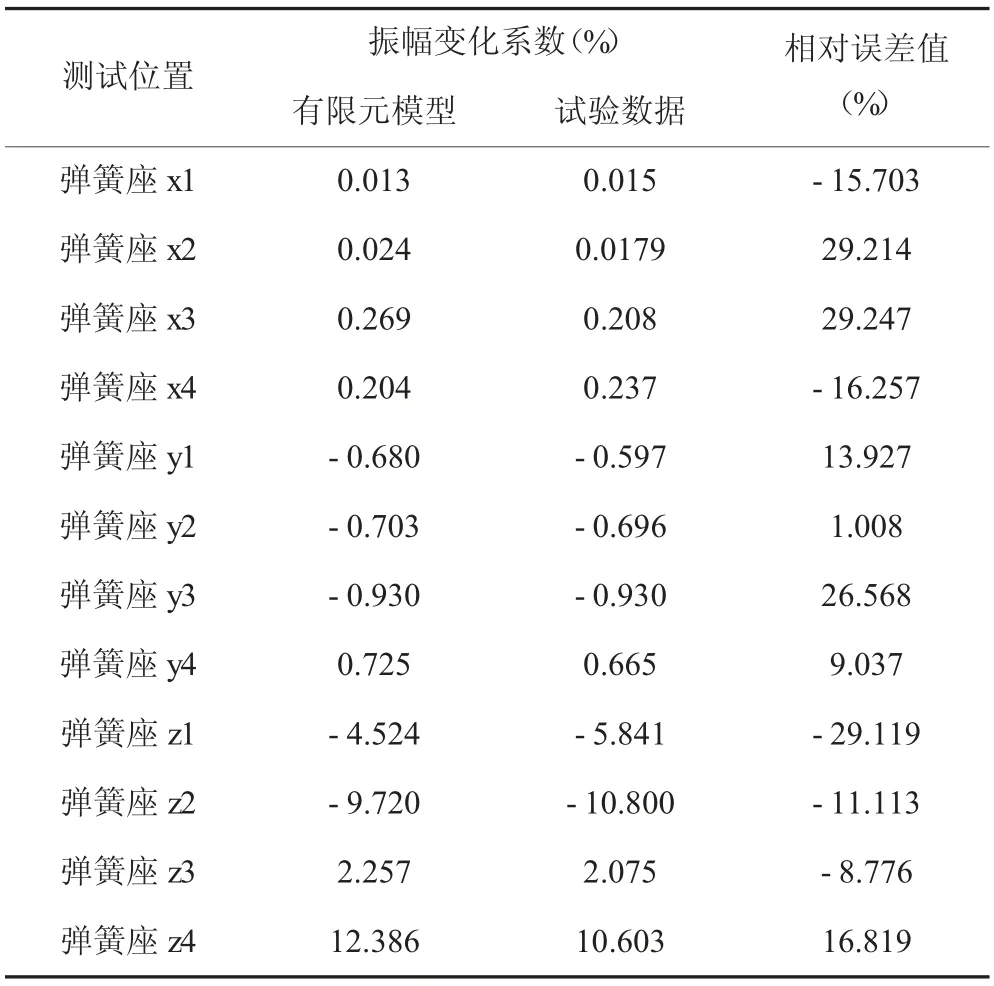
表2 有限元仿真数据与试验数据的对比表格

在针对单个弹簧故障试验时，通过试验仪器采集得到矿用振动筛弹簧座在三个方向上的振幅，其信号数据可反应出弹簧故障信息。虽然有限元仿真数据与试验数据之间存在着一定误差，究其原因是在运用Ansys软件建立有限元模型时，人为的对矿用振动筛模型进行了简化，导致理论模型与实际质心位置、激振力方向等参数均不一致。通过对有限元仿真数据与试验数据的对比可以发现，有限元仿真数据比较接近试验数据，而且反映出来的振幅变化规律也很接近，表明弹簧永久性变形故障可依据有限元仿真分析的振幅变化规律做出判断，首先通过仿真分析得到弹簧的振幅规律，以提取到弹簧故障信息的数据，以诊断弹簧故障问题，同时可以较为客观的反映出矿用振动筛弹簧的实际应用工况状态，也能够有效地指导设计人员的设计及设备操作人员的日常维修和保养工作。

4 结论

本文主要针对矿用振动筛在实际工作过程中突出的弹簧永久性变形的故障问题，通过采用Ansys软件建立矿用振动筛有限元仿真模型，并进行了理论研究分析（静力学分析和模态分析），再经过矿用振动筛弹簧永久变形故障试验验证，对比分析有限元模型仿真数据和试验数据，结果表明：基于Ansys软件的有限元模型仿真分析的结果与试验测量结果较为接近，而且反映出的矿用振动筛弹簧振幅变化规律亦相接近，证明有限元模型仿真分析得到的振幅规律可以作为弹簧故障信息的判断依据。