Hom-李超三系的上同调和形变

郭 双 建

(贵州财经大学数学与统计学院，贵阳 550025)

Hom-李代数起源于向量场上李代数的离散型量子q-形变理论，其概念是由Hartwig等学者在研究拟李代数时引进的[1-2]. 随后，Hom-型代数引起大量学者的研究兴趣[3-6]，比如，生云鹤教授系统研究了Hom-李代数的表示[7]等. 其一些推广概念，如Hom-李超代数，Hom李着色代数、Hom李三系，3-Hom李代数等相继出现，它们的诸多性质也相继被研究．

李超三系是李三系的自然推广，其最早源于在高能物理场上三元乘法求解Yang-Baxter方程的理论研究[8-9]. 随后，文献[10]刻画了拟-经典李超三系的概念，讨论了其与Yang-Baxter方程的求解的联系，并且给出了若干具体例证. 文献[11]讨论了李超三系的上同调和Nijenhuis 算子. 虽然李超三系的概念引入的时间不长，但是它已经被许多学者接受.但遗憾的是，除了文献[12]刻画了Hom李超三系的导子之外，对Hom李超三系的性质研究还不多，这也是本文的研究出发点.

设T为Hom-李超三系.本文主要刻画其上的若干代数性质，并引入了T的上同调和上边界算子，最后利用上同调方法讨论了T的形变．

1Hom-李超三系的上同调

定义1[12]保积Hom-李超三系(T，[·，·，·])是一个Z2分次向量空间T，伴有三元运算[·，·，·]:T×T×T→T和线性映射φ:T→T，φ([x，y，z])=[φ(x)，φ(y)，φ(z)]使得下列等式成立

|[x，y，z]|=(|x|+|y|+|z|)(mod 2);

(1)

[y，x，z]=-(-1)|x||y|[x，y，z];

(2)

(-1)|x||z|[x，y，z]+(-1)|y||x|[y，z，x]+

(-1)|z||y|[z，x，y]=0;

(3)

[φ(x)，φ(y)，[z，u，v]]=

[[x，y，z]，φ(u)，φ(v)]+

(-1)|z|(|x|+|y|)[φ(z)，[x，y，u]，φ(v)]+

(-1)(|x|+|y|)(|z|+|u|)[φ(z)，φ(u)，[x，y，v]].

(4)

其中，齐次元x，y，z，u，v∈T.以|x|表示x的Z2次数. 在本文中，出现|x|时，均默认x为T中的齐次元．

如果三线性映射χ:(T，[·，·，·]，φ)→(T′，[·，·，·]′，φ′)为Z2-空间上的态射，且满足χ([x，y，z])=[χ(x)，χ(y)，χ(z)]′和χφ=φ′χ，则称χ为Hom-李超三系的同态．

定义2设T为保积Hom-李超三系，V为Z2-分次向量空间和A∈End(V). 若双线性映射θ:T⊗T→End(V)满足下列条件: 对任意的x，y，z，u∈T，

θ(φ(x)，φ(y))A=Aθ(x，y)，

(5)

(-1)(|x|+|y|)(z+|u|)θ(φ(z)，φ(u))θ(x，y)-

(-1)|x||y|+|u|(|z|+|x|)θ(φ(y)，φ(u))θ(x，z)-

θ(φ(x)，[y，z，u])A+

(-1)|x|(|y|+|z|)D(φ(y)，φ(z))θ(x，u)=0，

(6)

(-1)(|x|+|y|)(|z|+|u|)θ(φ(z)，φ(u))D(x，y)-

D(φ(x)，φ(y))θ(z，u)+θ([x，y，z]，φ(u))A+

(-1)|z|(|x|+|y|)θ(φ(z)，[x，y，u])A=0.

(7)

其中，D(x，y)=(-1)|x||y|θ(y，x)-θ(x，y)，则称(V，θ)为T的表示，即V为T-模．

例1设T为保积Hom-李超三系.定义θ:T⊗T→End(V)为

θ(x，y)(z)=(-1)|z|(|x|+|y|)[z，x，y].

易知，D(x，y)(z)=[x，y，z]. 此时，(T，θ)为T的伴随表示．

命题1设T为保积Hom-李超三系，(V，θ)为T的一个表示，则T⊗V为保积Hom-李超三系．

证明对任意的(x，u)，(y，v)，(z，w)∈T⊗V，定义三线性积[·，·，·]:(T⊗V)⊗(T⊗V)⊗(T⊗V)→(T⊗V)为

[(x，u)，(y，v)，(z，w)]=
([x，y，z]，(-1)|x|(|y|+|z|)θ(y，z)(u)-
(-1)|y||z|θ(x，z)(v)+D(x，y)(w))，

其中，|(x，u)|=|x|．

由于T为保积Hom-李超三系，容易验证(1)成立．

对于(2)，令(x，u)，(y，v)，(z，w)∈T⊗V并计算如下，

-(-1)|x||y|[(y，v)，(x，u)，(z，w)]=
-(-1)|x||y|([y，x，c]，(-1)|y|(|x|+|z|)·
θ(x，z)(v)-(-1)|x||z|θ(y，z)(u)+
D(y，x)(w))=
(-(-1)|x||y|[y，x，c]，
-(-1)|y||z|θ(x，z)(v)-
(-1)|x|(|y|+|z|)θ(y，z)(u)-
(-1)|x||y|D(y，x)(w))=
([x，y，z]，(-1)|x|(|y|+|z|)·
θ(y，z)(u)-(-1)|y||z|θ(x，z)(v)+
D(x，y)(w))=[(x，u)，(y，v)，(z，w)]，

由于

-(-1)|x||y|[y，x，w]=[x，y，w]=

D(x，y)(w)，

所以最后一个等式成立．

对于(3)，有

(-1)|x||z|[(x，u)，(y，v)，(z，w)]+

(-1)|y||x|[(y，v)，(z，w)，(x，u)] +

(-1)|z||y|[(z，w)，(x，u)，(y，v)]=

((-1)|x||z|[x，y，z]+(-1)|y||x|[y，z，x]+

(-1)|z||y|[z，x，y]，Ω)=(0，Ω)，

其中，

Ω=(-1)|x||y|θ(y，z)(u)-

(-1)(|x|+|y|)|z|θ(x，z)(v)+

(-1)|x||z|D(x，y)(w)+

(-1)|y||z|θ(z，x)(v)-

(-1)(|y|+|z|)|x|θ(y，x)(w)+

(-1)|b||a|D(y，z)(u)=

(-1)|x||y|θ(y，z)(u)+

(-1)|y||z|θ(z，x)(v)+

(-1)|z||y|θ(x，y)(w)-

(-1)|x||z|θ(x，y)(w)+

(-1)|y||x|θ(y，z)(u)-

(-1)|y||z|θ(z，x)(v)=0，

则有

(-1)|x||z|[(x，u)，(y，v)，(z，w)]+
(-1)|y||x|[(y，v)，(z，w)，(x，u)]+

(-1)|z||y|[(z，w)，(x，u)，(y，v)]=(0，0).

对于(4)，令(x，u)，(y，v)，(z，w)，(s，m)，(p，n)∈T⊗V.首先，计算如下，

[[(x，u)，(y，v)，(z，w)]，(φ+A)(s，m)，

(φ+A)(p，n)]=[([x，y，z]，

(-1)|x|(|y|+|z|)θ(y，z)(u)-

(-1)|y||z|θ(x，z)(v)+D(x，y)(w))·

(φ+A)(s，m)，(φ+A)(p，n)] =

([[x，y，z]，φ(s)，φ(p)]，Π1)，

其中，

Π1=(-1)(|x|+|y|+|z|)(|s|+|p|)·

(-1)|x|(|y|+|z|)θ(φ(s)，φ(p))θ(y，z)(u)-

(-1)(|x|+|y|+|z|)(|s|+|p|)(-1)|y||z|·

θ(φ(s)，φ(p))θ(x，z)(v)+

(-1)(|x|+|y|+|z|)(|s|+|p|)·

θ(φ(s)，φ(p))D(x，y)(w)-

(-1)|y||z|θ([x，y，z]，φ(p))θ(x，z)A(m)+

D([x，y，z]，s)A(n)，

其次，计算

(-1)|z|(|x|+|y|)(φ+A)[(z，w)，
[(x，u)，(y，v)，(s，m)]，(φ+A)(p，n)]=
[(-1)|z|(|x|+|y|)(φ+A)(z，w)·
([x，y，s]，(-1)|x|(|y|+|s|)θ(y，s)(u)-
(-1)|y||s|θ(x，s)(v)+D(x，y)(m))，
(φ+A)(p，n)]=
((-1)|z|(|x|+|y|)[φ(z)，[x，y，s]，φ(p)]，Π2)，

其中，

Π2=-(-1)(|x|+|y|+|s|)|p|·

(-1)|z|(|x|+|y|)+|x|(|y|+|s|)·

θ(φ(z)，φ(p))θ(y，s)(u)+

(-1)(|x|+|y|+|s|)|p|·

(-1)|z|(|x|+|y|)+|y||s|·

θ(φ(z)，φ(p))θ(x，s)(v)+

(-1)(|x|+|y|+|s|+|p|)|z|·

(-1)|z|(|x|+|y|)θ([x，y，s]，φ(p))A(w)-

(-1)(|x|+|y|+|s|)|p|(-1)|z|(|x|+|y|)·

θ(φ(z)，φ(p))D(x，s)(m)+

(-1)|z|(|x|+|y|)D(φ(z)，[x，y，s])A(n)，

第三，再计算

(-1)(|x|+|y|)(|z|+|s|)·
[(φ+A)(z，w)，(φ+A)(s，m)，
[(x，u)，(y，v)，(p，n)]]=
(-1)(|x|+|y|)(|z|+|s|)·
[(φ+A)(z，w)，(φ+A)(s，m)，
([x，y，p]，(-1)|x|(|y|+|p|)·
θ(y，p)(u)-(-1)|y||p|θ(x，p)(v)+
D(x，y)(n))]=
((-1)(|x|+|y|)(|z|+|s|)·
[φ(z)，φ(s)，[x，y，p]]，Π3)，

其中，

Π3=(-1)(|x|+|y|)(|z|+|s|)·

(-1)|x|(|y|+|p|)D(φ(z)，φ(s))θ(y，p)(u)-

(-1)(|x|+|y|)(|z|+|s|)(-1)|y||p|·

D(φ(z)，φ(s))θ(x，p)(v)+

(-1)(|x|+|y|)(|z|+|s|)·

(-1)(|x|+|y|+|p|)|z|θ(φ(s)，[x，y，p])A(w)-

(-1)(|x|+|y|)(|z|+|s|)·

(-1)(|x|+|y|+|p|)|s|·

θ(φ(z)，[x，y，p])A(m)+

(-1)(|x|+|y|)(|z|+|s|)·

D(φ(z)，φ(s))D(x，y)(n)，

第四，计算

[(φ+A)(x，u)，(φ+A)(y，v)，
[(z，w)，(s，m)，(p，n)]]=
[(φ+A)(x，u)，(φ+A)(y，v)，
([z，s，p]，(-1)|z|(|s|+|p|)·
θ(s，p)(w)-(-1)|s||p|θ(z，p)(m)+
D(z，s)(n))]=([x，y，[z，s，p]]，Π4)，

其中，

Π4=(-1)|x|(|y|+|z|+|s|+|p|)·

θ(φ(y)，[z，s，p])A(u)-

(-1)|y|(|z|+|s|+|p|)θ(φ(x)，[z，s，p])A(v)+

(-1)|z|(|s|+|p|)D(α(z)，α(s))θ(s，p)(w)-

(-1)|s||p|D(α(z)，α(s))θ(z，p)(m)

+D(φ(z)，φ(s))D(z，s)(n)，

最后，由等式(5)，(6)和(7)，可得

[[(x，u)，(y，v)，(z，w)]，
(φ+A)(s，m)，φ(α+A)(p，n)]+
(-1)|z|(|x|+|y|)[(φ+A)(z，w)，
[(x，u)，(y，v)，(s，m)]，(φ+A)(p，n)]+
(-1)(|x|+|y|)(|z|+|s|)[(φ+A)(z，w)，
(φ+A)(s，m)，[(x，u)，(y，v)，(s，m)]]=
([[x，y，z]，φ(s)，φ(p)]+
(-1)|z|(|x|+|y|)[φ(z)，[x，y，s]，φ(p)]+
(-1)(|x|+|y|)(|z|+|s|)[φ(z)，φ(s)，
[x，y，p]]，Π1+Π2+Π3)=
([φ(x)，φ(y)，[z，s，p]]，Π4)=
[(φ+A)(x，u)，(φ+A)(y，v)，
[(z，w)，(s，m)，(p，n)]]，

证毕．

定义3设T为保积Hom-李超三系，V为T-模. 如果存在n-线性映射χ:T×T×…×T→T满足下列条件：

Aχ(x1，x2，…，xn)=χ(φ(x1)，φ(x2)，…，φ(xn))，

(8)

χ(x1，x2，…，x，y，…，xn)=

-(-1)|x||y|χ(x1，x2，…，x，y，…，xn)，

(9)

-(-1)|x||z|χ(x1，x2，…，xn-3，x，y，z)+

(-1)|y||x|χ(x1，x2，…，xn-3，x，z，y)+

(-1)|z||y|χ(x1，x2，…，xn-3，z，x，y)=0.

(10)

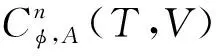
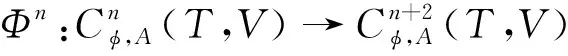
Φ2n-1χ(x1，…，x2n+1)=

(-1)(|x2n|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn-1(x2n)，φn-1(x2n+1))χ(x1，…，x2n-1)-

(-1)(|x2n-1|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-2|)+|x2n+1||x2n|·

θ(φn-1(x2n-1)，φn-1(x2n+1))χ(x1，…，x2n-1，x2n)+

D(φn-1(x2k-1)，φn-1(x2k))·

[x2k-1，x2k，xj]，…，φ(x2n+1)).

Φ2nχ(x1，…，x2n+1)=

(-1)(|x2n|+|x2n+1|)(|χ|+|y|+|x1|+|x2|+…+|x2n-1|)·

θ(φn(x2n)，φn(x2n+1))χ(y，x1，…，x2n-1)-

(-1)(|x2n-1|+|x2n+1|)(|χ|+|y|+|x1|+|x2|+…+|x2n|)·

θ(φn(x2n-1)，φn(x2n+1))χ(y，x1，…，x2n-2，x2n)+

D(φn(x2k-1)，φn(x2k))·

不难验证Φnχ满足(9)和(10). 要验证Φnχ满足(8)，使得Φnχ是良定义的，事实上，只需验证

A(Φ2n-1χ(x1，…，x2n-1))=(Φ2n-1χ(φ(x1)，…，

φ(x2n-1))).Φ2n-1χ(φ(x1)，…，φ(x2n-1))=

(-1)(|x2n|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn(x2n)，φn(x2n+1))χ(φ(x1)，…，φ(x2n-1))-

(-1)(|x2n-1|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-2|)+|x2n+1||x2n|·

θ(φn(x2n-1)，φn(x2n+1))χ(φ(x1)，…，φ(x2n-2)，

(-1)(|x2k-1|+|x2k|)(|χ|+|x1|+|x2|+…+|x2k-2|)·

φ([x2k-1，x2k，xj])，…，φ2(x2n+1))=

(-1)(|x2n|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn(x2n)，φn(x2n+1))A(χ(x1，…，x2n-1))-

(-1)(|x2n-1|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-2|)+|x2n+1||x2n|·

θ(χn(x2n-1)，χn(x2n+1))A(χ(x1，…，x2n-1，x2n))+

Aθ(φn-1(x2n)，φn-1(x2n+1))(χ(x1，…，x2n-1))-

A(-1)(|x2n|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn-1(x2n-1)，φn-1(x2n+1))(χ(x1，…，x2n-1，x2n))+

D(φn-1(x2k-1)，φn-1(x2k))·

A(Φ2n-1χ(x1，…，x2n+1)).

定理1设T为保积Hom-李超三系，V为T-模,则上边界算子Φn满足Φn+2Φn=0．

证明由上边界算子的定义可知，Φ2n+1Φ2n-1=0可推出Φ2n+2Φ2n=0. 因此只需验证Φ2n+1Φ2n-1=0，n=1，2，3，… ．

其中，

(-1)(|x2n|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn-1(x2n)，φn-1(x2n+1))χ(x1，…，x2n-1)-

(-1)(|x2n-1|+|x2n+1|)(|f|+|x1|+|x2|+…+|x2n-2|)+|x2n+1||x2n|·

θ(φn-1(x2n-1)，φn-1(x2n+1))χ(x1，…，x2n-1，x2n)，

χ(x1，…，x2n+3)=

(-1)(|x2n+2|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n+1|)·

θ(φn(x2n+2)，φn(x2n+3))Φ2n-1χ(x1，…，x2n+1)-

(-1)(|x2n+1|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n|)+|x2n+2||x2n+3|·

θ(φn(x2n+1)，φn(x2n+3))Φ2n-1χ(x1，…，x2n，x2n+2)+

(-1)(|x2k-1|+|x2k|)(|χ|+|x1|+|x2|+…+|x2k-2|)·

(-1)(|x2n+2|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n+1|)·

θ(φn(x2n+2)，φn(x2n+3)).

(a1) ((-1)(|x2n|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn-1(x2n)，φn-1(x2n+1))χ(x1，…，x2n-1)

(a2) -(-1)(|x2n-1|+|x2n+1|)(|χ|+|x1|+|x2|+…+|x2n-2|)+|x2n+1||x2n|·

θ(φn-1(x2n-1)，φn-1(x2n+1))χ(x1，…，x2n-1，x2n)+

D(φn-1(x2k-1)，φn-1(x2k))

(-1)(|x2n+1|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n|)+|x2n+2||x2n+3|·

θ(φn(x2n+1)，φn(x2n+3))

(a3) (-1)(|x2n|+|x2n+2|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn-1(x2n)，φn-1(x2n+2))χ(x1，…，x2n-1)

(a4) -(-1)(|x2n-1|+|x2n+2|)(|χ|+|x1|+|x2|+…+|x2n-2|)+|x2n+2||x2n|·

θ(φn-1(x2n-1)，φn-1(x2n+2))χ(x1，…，x2n-2，x2n)+

D(φn-1(x2k-1)，φn-1(x2k))

…，[x2k-1，x2k，xj]，…，φ(x2n)，φ(x2n+2))+

D(φn(x2k-1)，φn(x2k))

(b3) (-1)(|x2n+2|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n+1|)·

(-1)(|x2n+1|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n|)+|x2n+2||x2n+3|·

θ(φn-1(x2n+1)，φn-1(x2n+3))

D(φn(x2n+1)，φn(x2n+2))·

(-1)(|x2n|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n-1|)·

θ(φn-1(x2n)，φn-1(x2n+3))

(a5)χ((x1，…，x2n-1))-

(-1)(|x2n-1|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n-2|)+|x2n||x2n+3|·

θ(φn-1(x2n-1)，φn-1(x2n+3))

(-1)(|x2n+2|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n+1|)·

θ(φn(x2n+2)，φn(x2n+3))

(b6)θ(φn(x2n+2)，φn-1[x2k-1，x2k，x2n+3])χ(φ(x1)，

(-1)(|x2n|+|x2n+1|+|x2n+2|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n-1|)

(a7)θ(φn(x2n)，φn-1[x2n+1，x2n+2，x2n+3])χ(φ(x1)，

(-1)(|x2n+1|+|x2n+3|)(|χ|+|x1|+|x2|+…+|x2n|)+|x2n+2||x2n+3|·

θ(φn(x2n+1)，φn(x2n+3))

(a8)θ(φn(x2n-1)，φn-1[x2n+1，x2n+2，x2n+3])χ(φ(x1)，…，φ(x2n-2)，φ(x2n))

由等式(6)和(8)，可知(a1)+···+(a8)=0; 由(7)和(8)，可知(b1)+···+(b8)=0;不难验证(c1)+(c2)=(d1)+(d2)=0. 因此

2Hom-李超三系的单参数形式形变

设T为保积Hom-李超三系，k[[t]]为变量t的幂级数环.假设T[[t]]是一组形式级数，其系数是向量空间T的元素．

定义5设T为保积Hom-李超三系，则T的单参数形式形变为一组幂级数

χt:T[[t]]×T[[t]]×T[[t]]→T[[t]]

为

φ(z))=φχt(x，y，z)，

(11)

其中，每一个χi为k-三线性映射χi:T×T×T→T和χ0(y1，y2，y3)=[y1，y2，y3]，满足下列条件：

|χt(y1，y2，y3)|=|y1|+|y2|+|y3|;

(12)

χt(y1，y2，y3)=

-(-1)|y1||y2|χt(y1，y2，y3);

(13)

-(-1)|y1||y3|χt(y1，y2，y3)+

(-1)|y2||y1|χt(y2，y3，y1)+

(-1)|y3||y2|χt(y3，y1，y2)=0;

(14)

χt(φ(y1)，φ(y2)，χt(y3，y4，y5))=

(-1)|y3|(|y1|+|y2|)χt(φ(y3)，

χt(y1，y2，y4)，φ(y5))+

χt(χt(y1，y2，y3)，φ(y4)，φ(y5))+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

χt(φ(y3)，φ(y4)，χt(y1，y2，y5)).

(15)

注记1等式(11)～(15)等价于

χt(φ(x)，φ(y)，φ(z))=φχt(x，y，z);

(16)

|χi(y1，y2，y3)|=|y1|+|y2|+|y3|;

(17)

χi(y2，y1，y3)=-(-1)|y1||y2|χi(y1，y2，y3);

(18)

(-1)|y1||y3|χi(y1，y2，y3)+

(-1)|y2||y1|χi(y2，y3，y1)+

(-1)|y3||y2|χi(y3，y1，y2)=0;

(19)

χi(α(y3)，χj(y1，y2，y4)，φ(y5))+

χi(χj(y1，y2，y3)，φ(y4)，φ(y5))+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

χi(φ(y3)，φ(y4)，χj(y1，y2，y5)).

(20)

χiχj(y1，y2，y3，y4，y5)+

χi(χj(y1，y2，y3)，φ(y4)，φ(y5))+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

χi(φ(y3)，φ(y4)，χj(y1，y2，y5)).

当n=1，等式(20)等价于χ0χ1+χ1χ0=0. 当n≥2，等式(20)等价于-(χ0χn+χnχ0)=χ1χn-1+χ1χn-2+…+χn-1χ1.

由χ0(y1，y2，y3)=[y1，y2，y3]，有

χ0χ1(y1，y2，y3，y4，y5)=

-D(φ(y1)，φ(y2)，χ(y3，y4，y5))-

(-1)(|y1|+|y2|)(|y3|+|y5|)+|y4||y5|·

D(φ(y3)，φ(y4)，χ(y1，y2，y5))+

(-1)(|y1|+|y2|+|y3|)(|y4|+|y5|)·

θ(φ(y4)，φ(y5))χ(y1，y2，y3)+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

D(φ(y3)，φ(y4)，χ(y1，y2，y5))=

-[φ(y1)，φ(y2)，χ1(y3，y4，y5)]+

(-1)|y3|(|y1|+|y2|)·

[φ(y3)，χ1(y1，y2，y4)，φ(y5)]+

[χ1(y1，y2，y3)，φ(y4)，φ(y5)]+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

[φ(y3)，φ(y4)，χ1(y1，y2，y5)]=

-D(φ(y1)，φ(y2)，φ(y3，y4，y5))-

(-1)(|y1|+|y2|)(|y3|+|y5|)+|y4||y5|·

D(φ(y3)，φ(y4)，χ(y1，y2，y5))+

(-1)(|y1|+|y2|+|y3|)(|y4|+|y5|)·

θ(φ(y4)，φ(y5))χ(y1，y2，y3)+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

D(φ(y3)，φ(y4)，χ(y1，y2，y5))，

类似的，有

χ1χ0(y1，y2，y3，y4，y5)=

-χ1(φ(y1)，φ(y2)，χ0(y3，y4，y5))-

(-1)|y3|(|y1|+|y2|)·

χ1(φ(y3)，χ(y1，y2，y4)，φ(y5))+

χ1(χ0(y1，y2，y3)，φ(y4)，φ(y5))+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

χ1(y3，y4，χ0(y1，y2，y5))=

-χ1(φ(y1)，φ(y2)，[y3，y4，y5])+

(-1)|y3|(|y1|+|y2|)·

χ1(φ(y3)，χ0(y1，y2，y4)，φ(y5))+

χ1([y1，y2，y3]，φ(y4)，φ(y5))+

(-1)(|y1|+|y2|)(|y3|+|y4|)·

χ1(φ(y3)，φ(y4)，y1，y2，y5)，

于是

(χ0χ1+χ1χ0)(y1，y2，y3，y4，y5)=

Φ3χ1(y1，y2，y3，y4，y5).

因此，由χ0χ1+χ1χ0=0，可得Φ3χ1=0. 也可得

-Φ3χn=χ1χn-1+χ2χn-2+…+χn-1χ1，

称χ1为χt的无穷小形变．

定义6设T为保积Hom-李超三系.如果存在k[[t]]-模形式同构

其中Ψt∘φ=φ∘Ψt:T→T为k-线性映射使得

∀y1，y2，y3∈T.

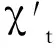
特别的，如果χ1=χ2=…=0，则称χ1=χ0为零形变. 如果χt～χ0，则称χt为微小形变. 如果每一个单参数形式形变χt均为微小的，则称T为Hom-分析刚性的．

其中，y1，y2，y3∈T. 比较上述等式两边t1的系数，有

χ1(y1，y2，y3)+Ψ1([y1，y2，y3])=

[y1，Ψ(y2)，y3]+[y1，y2，Ψ(y3)]，

进一步,

[Ψ1(y1)，y2，y3]+[y1，Ψ1(y2)，y3]+

[y1，y2，Ψ1(y3)]-Ψ1([y1，y2，y3])=

(-1)|y1|(|y2|+|y3|)θ(y2，y3)Ψ1(y1)-

Ψ1([y1，y2，y3])+D(y1，y2)Ψ1(y3)-

(-1)|y2||y3|θ(y1，y3)Ψ1(y2)=

Φ1Ψ1(y1，y2，y3).

Φ3χn=χ1φn-1+χ2χn-2+…+χn-1χ1=0.

令Ψt=idT-ηntn，则

χ0(y1，y2，y3)-{χ0(ηn(y1)，y2，y3)+

χ0(y1，ηn(y2)，y3)+χ0(y1，y2，ηn(y3))}tn+

{χ0(ηn(y1)，ηn(y2)，y3)+

χ0(y1，ηn(y2)，ηn(y3))+

χ0(y1，ηn(y2)，ηn(y3))}t2n+

χ0(ηn(y1)，ηn(y2)，ηn(y3))t3n+

χ0(y1，y2，ηn(y3))}ti+n+

χi(y1，ηn(y2)，ηn(y3))+

χi(y1，ηn(y2)，ηn(y3))}ti+2n-

于是，

χ′1(y1，y2，y3)=…=χ′n-1(y1，y2，y3)=0,

χn(y1，y2，y3)-[ηn(y1)，y2，y3]-

[y1，ηn(y2)，y3]-[y1，y2，ηn(y3)]=

χn(y1，y2，y3)-

(-1)|y1|(|y2|+|y3|)θ(y2，y3)ηn(y1)+

(-1)|y2||y3|θ(y1，y3)ηn(y2)-

D(y1，y2)ηn(y3)，

因此，推出

χn(y1，y2，y3)-Φ1ηn(y1，y2，y3)=0.