复杂噪声场景下的电子音乐信号智能检测算法设计

许晶晶

摘  要： 电子音乐信号检测有利于音乐的分类和后续处理，针对当前电子音乐信号检测方法没有考虑噪声对电子音乐信号检测结果的干扰，导致电子音乐信号检测错误率大，检测时间长，无法满足现代大规模电子音乐信号检测的实际要求。为了解决当前电子音乐信号检测过程中存在的一些局限性，提出一种复杂噪声场景下的电子音乐信号智能检测算法。首先分析电子音乐信号智能检测的原理，引入小波变换对电子音乐信号中的噪声进行抑制;然后从消噪的电子音乐信号中提取特征，并根据电子音乐信号类型构建学习样本;最后引入最小二乘支持向量机对电子音乐信号智能检测模型进行构建，分析电子音乐信号的变化特点，并对其参数进行相应的优化。仿真实验结果表明，对于复杂噪声场景下的电子音乐信号，文中方法可以获得较高精度的检测结果，检测时间也明显得到了减少，获得了比其他方法更优的电子音乐信号，对复杂噪声具有较强的鲁棒性。

关键词： 电子音乐信号检测; 智能检测算法; 检测原理分析; 噪声抑制; 模型构建; 参数优化

中图分类号： TN911.23?34; TP391                  文献标识码： A                   文章编号： 1004?373X（2020）19?0049?04

Abstract： Electronic music signal detection is conducive to music classification and follow?up processing. For the current electronic music signal detection method， the interference of noise on the electronic music signal detection results is not considered， which makes the electronic music signal detection error rate large and detection time long， and is unable to meet the actual requirements of large?scale modern electronic music signal detection. In order to solve some limitations existing in the process of the current electronic music signal detection， an intelligent detection algorithm of electronic music signal in complex noise scene is proposed. The principle of intelligent detection of electronic music signal is analyzed. The wavelet transform is introduced to suppress the noise in electronic music signal， and then the features of the denoised electronic music signal are extracted. The learning samples are constructed according to the types of electronic music signal. The least square support vector machine is introduced to construct the intelligent detection model of electronic music signal， analyze the changes of electronic music signal， and carried out corresponding optimization of the parameters. The simulation results show that， for the electronic music signal in the complex noise scene， the method proposed in this paper can obtain high?precision detection results， and its detection time is significantly reduced， and its electronic music signals are better than those of other methods， which has strong robustness to complex noise.

Keywords： electronic music signal detection; intelligent detection algorithm; detection principle analysis; noise suppression; model establishment; parameter optimization

0  引  言

随着人们生活水平的不断提高以及微电子技术、语音技术的不断发展，可以通过计算机合成一个音乐，称之为电子音乐[1?3]。由于每个人都可以合成电子音乐，使得电子音乐信号数据呈爆炸式增加，给人们选择自己最喜欢的电子音乐信号带来了困难，而电子音乐信号检测可帮助人们快速、准确地选择电子音乐，因此电子音乐信号检测具有十分重要的研究意义[4?6]。

由于学者们的大量投入以及各行各业的关注，当前电子音乐信号检测算法很多[7?9]。相对于其他类型算法，人工神经网络和支持向量机的电子音乐信号检测算法最常用，它们均属于人工智能领域的新型技术[10?12]，在电子音乐信号检测实际应用中，人工神经网络和支持向量机均存在一些难以克服的问题，如：人工神经网络的电子音乐信号检测错误率高，电子音乐信号检测结果极不稳定，人们经常得不到真正需要的电子音乐信号检测结果;支持向量机的电子音乐信号检测速度慢，对于大规模电子音乐信号来说，通常无法在有效时间内得到电子音乐信号检测结果。同时它们均没有考虑噪声对电子音乐信号检测结果的干扰，对噪声鲁棒性差，影响音乐的分类和后续处理[13?15]。

为了提高电子音乐信号检测效果，本文提出了复杂噪声场景下的电子音乐信号智能检测算法，并对其优越性和通用性进行了测试，结果表明，本文算法的电子音乐信号检测精度、智能化程度高，而且电子音乐信号检测时间短。

1  电子音乐信号智能检测算法设计

1.1  电子音乐信号的噪声抑制

为了对电子音乐信号中的噪声进行最大程度的抑制，采用小波分析算法去除电子音乐信号中的噪声。设[f（t）∈L2（R）]，连续小波[Ψ（t）]应该满足如下条件：

式中[τ]为位移。

电子音乐信号采用计算机进行处理，因此其属于离散信号，设[a=2-j]，[τ=2-jk]，得到离散小波如下：

对电子音乐信号抑制的步骤如下：

Step1：采用小波分析对原始电子音乐信号进行分解，得到多个电子音乐子信号，每一个电子音乐子信号含有一个小波系数，根据频率高低对电子音乐子信号进行排列，第一个电子音乐子信号的小波系数向量表示为[c1]，那么所有子信号小波系数向量集为：[C=[c1，c2，…]]。

Step2：电子音乐信号向量集可以划分为两部分：有用的电子音乐信号（[S]）和噪声（[U]），即：

Step3：计算电子音乐信号噪声标准方差（[σ]），然后设置一个阈值（[δ]），两者之间的关系可描述为：

设大于[δ]的子信号向量小波系数值设置为0，其他保持不变，得到电子音乐信号小波系数的新向量为：

Step4：采用小波分析對电子音乐信号小波系数进行重建，得到没有噪声的电子音乐信号。

1.2  电子音乐信号特征提取

由于不同的电子音乐信号有不同的特征，因此电子音乐信号特征提取十分重要，本文采用Mel频率倒谱系数描述电子音乐信号。Mel频率和实际频率[（f）]之间的关系可以描述为：

Mel频率倒谱系数提取电子音乐信号特征的具体步骤如下：

Step1：对电子音乐信号进行预加重、分帧操作，采用傅里叶变换对电子音乐信号进行处理，从而可以得到电子音乐信号的频谱能量系数。

Step2：以Mel刻度分布为基础，用三角滤波器组对电子音乐信号的频谱能量系数进行卷积操作，并对结果进行离散余弦变换，选择12个系数进行时倒谱加权操作，从而得到电子音乐信号特征的Mel频率倒谱系数。

Step3：对电子音乐信号特征的Mel频率倒谱系数进行一次差分操作，又产生12个系数，共得到24个Mel频率倒谱系数，并将它们作为电子音乐信号的检测特征。

1.3  最小二乘支持向量机建立电子音乐信号检测分类器

最小二乘支持向量机的训练时间明显短于支持向量机的训练时间，而且学习性能要优于人工神经网络的学习性能，因此采用最小二乘支持向量机建立电子音乐信号检测分类器。电子音乐信号检测的分类平面为：

对式（1）变化处理，可以得到：

式中[γ]为最小二乘支持向量机的正则化参数。

对式（8）进行求解，由于具有相应的约束条件，使得求解过程比较复杂，为了加快求解速度，将其变化为无约束形式，具体如下：

最小二乘支持向量机建立电子音乐信号检测分类器只能对两类电子音乐进行检测，而实际上电子音乐信号有多种类型，因此采用图1形式可以建立多种电子音乐信号检测的分类器。

在最小二乘支持向量机的电子音乐信号检测过程中，参数[γ]和[σ]对电子音乐信号检测结果的影响程度很大，而传统方法主要采用人工方式凭经验实现，导致电子音乐信号检测效果并非真正的达到最优，为此本文采用粒子群算法解决难题，以得到更优的电子音乐信号检测结果。

1.4  电子音乐信号检测分类器参数优化

1.5  复杂噪声场景下的电子音乐信号智能检测原理

复杂噪声场景下的电子音乐信号智能检测算法的工作原理为：首先收集电子音乐信号，并引入小波变换对电子音乐信号中的噪声进行抑制;然后从消噪的电子音乐信号中提取特征，并根据电子音乐信号类型构建学习样本;最后引入最小二乘支持向量机对电子音乐信号智能检测模型进行构建，分析电子音乐信号变化特点，并对其参数进行相应的优化，具体如图2所示。

2  电子音乐信号智能检测性能测试

2.1  测试平台

为了分析本文设计的复杂噪声场景下的电子音乐信号智能检测有效性，对其进行仿真测试，测试的平台如表1所示。

2.2  对比算法及测试数据

为了测试本文设计的复杂噪声场景下的电子音乐信号智能检测算法的优越性，选择文献[13?14]的电子音乐信号智能检测算法进行对照实验，它们的测试平台相同。采用流行音乐作为对象，测试数据采集两类电子音乐信号：一类是不含有噪声的电子音乐信号;另一类是含有噪声的电子音乐信号。每一种方法进行5次仿真实验，电子音乐信号测试数据如表2所示。

2.3  结果与分析

2.3.1  电子音乐信号检测精度分析

采用3种电子音乐信号智能检测算法分别对无噪和含有噪声的电子音乐信号进行检测，统计它们的精度结果如图3和图4所示。对图3和图4的无噪和含有噪声的电子音乐信号检测精度进行对比和分析可知：

1） 对于无噪和含有噪声的电子音乐信号，文献[13]对电子音乐信号检测精度平均值分别为86.83%和81.0%，无噪的电子音乐信号检测精度要略高于含有噪声的电子音乐信号，这主要是因为其没有引入噪声消除技术，无法抑制噪声对电子音乐信号检测结果的干扰，因此电子音乐信号检测精度有待进一步提高。

2） 对于无噪和含有噪声的电子音乐信号，文献[14]对电子音乐信号检测精度平均值分别为91.39%和86.09%，电子音乐信号检测精度难以满足电子音乐信号实际处理的要求，这是因为其没有解决最小二乘支持向量机参数优化的问题，导致电子音乐信号检测错误率比较高。

3） 无论无噪或者是含有噪声的电子音乐信号，本文算法的检测精度平均值均要高于文献[13?14]的算法，这是因为本文算法引入了噪声消除算法，去掉了电子音乐信号中的噪声，获得了质量高的电子音乐信号，同时解决了电子音乐信号检测过程中的参数优化难题，降低了电子音乐信号的检测误差，获得理想的电子音乐信号检测结果，可以满足电子音乐信号处理的实际要求。

2.3.2  电子音乐信号检测效率分析

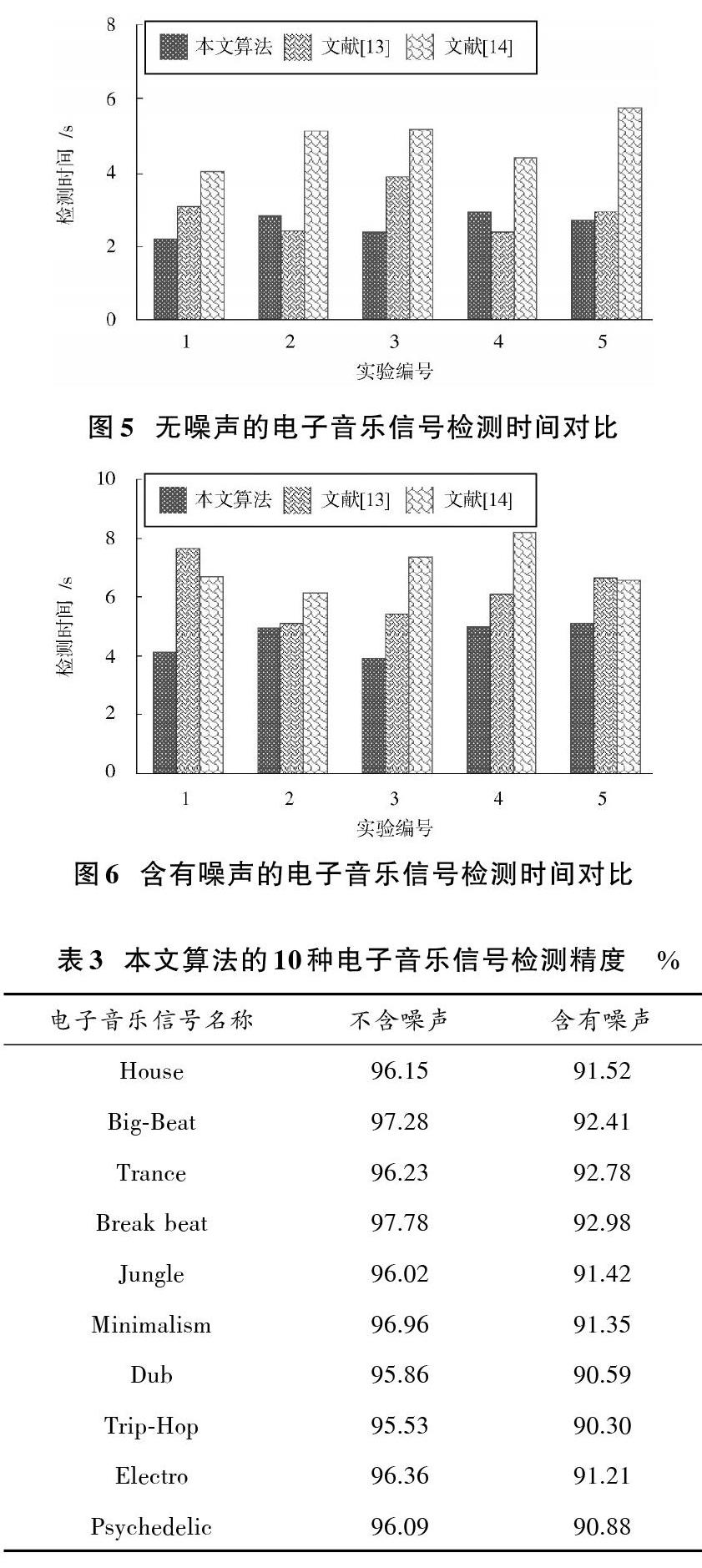
对于现代海量的电子音乐信号，检测效率十分关键，因此统计每一次实验的电子音乐信号检测时间，结果如图5和图6所示。从图5和图6可以发现，对于无噪和含有噪声的电子音乐信号，文献[13]的电子音乐信号检测时间平均值分别为2.97 s和6.20 s，文献[14]的电子音乐信号检测时间平均值分别为4.93 s和7.02 s，而本文算法的电子音乐信号检测时间平均值分别为2.63 s和4.63 s，本文算法的电子音乐信号检测时间明显减少，电子音乐信号检测效率相应提升，这与现代电子音乐信号向大规模发展的方向相适应。

2.3.3  电子音乐信号检测算法的通用性

為了测试本文电子音乐信号检测算法的通用性，选择当前流行的10种电子音乐信号作为研究对象，对它们分别进行检测，统计每一种电子音乐信号检测精度，结果如表3所示。从表3可以发现，对于10种电子音乐信号，本文算法的检测精度均超过90%，这表明本文算法具有很好的通用性。

3  结  语

针对当前电子音乐信号检测方法存在检测错误率大，检测时间长等局限性，本文提出一种复杂噪声场景下的电子音乐信号智能检测算法。仿真实验结果表明，对于复杂噪声场景下的电子音乐信号，本文方法获得了理想的检测结果，检测效率高，可以应用于实际的电子音乐信号分析和研究中。

参考文献

[1] 石宇加.电子音乐创作中效果器应用研究：以Digital performer为例[J].音乐时空，2011（10）：56?58.

[2] 李洪伟，李海峰，马琳，等.音乐欣赏中脑对音乐属性变化加工规律的脑电研究[J].复旦学报（自然科学版），2018，57（3）：385?392.

[3] 熊梅，张天骐，张婷，等.结合HPSS的非负矩阵音乐分离方法[J].计算机工程与设计，2018，39（4）：1089?1094.

[4] 桂文明，刘睿凡，陶玉婷，等.一种新型音乐速度谱图的生成算法[J].复旦学报（自然科学版），2018，57（3）：379?384.

[5] 张一彬，周杰，边肇祺，等.基于内容的音频与音乐分析综述[J].计算机学报，2007，30（5）：712?728.

[6] 陈芳，李伟，李晓强.基于小波包最优基的音乐指纹提取算法[J].计算机工程，2009，35（9）：236?237.

[7] 李丽娟，叶茂，赵欣.基于高斯混合模型流行音乐中歌唱部分的智能检测[J].小型微型计算机系统，2009，30（5）：1017?1020.

[8] 张天，张天骐，葛宛营，等.基于2DFT变换的伴奏音乐分离方法[J].信号处理，2019，35（10）：1708?1713.

[9] 赵志成，方力先.基于混沌理论的音乐信号非线性特征研究[J].振动与冲击，2019，38（3）：39?43.

[10] 孙慧芳，龙华，邵玉斌，等.基于过零率及频谱的语音音乐分类算法[J].云南大学学报（自然科学版），2019，41（5）：925?931.

[11] 刘迪，关欣，李锵，等.基于鲁棒主成分分析的音乐信号降噪[J].计算机工程，2016，42（9）：292?296.

[12] 张天骐，熊梅，张婷，等.结合区分性训练深度神经网络的歌声与伴奏分离方法[J].声学学报，2019，44（3）：393?400.

[13] 胡昭华，余媛媛.深度卷积神经网络在音乐风格识别中的应用[J].小型微型计算机系统，2018，39（9）：1932?1936.

[14] 周婧，范凌云.基于最小二乘支持向量机的电子音乐识别研究[J].现代电子技术，2018，41（9）：109?112.

[15] 王蒙蒙，关欣，李锵.基于鲁棒音阶特征和测度学习SVM的音乐和弦识别[J].信号处理，2017，33（7）：943?952.