高放废物处置多孔多罐热力耦合近场效应研究

高俊义

(延安大学 建筑工程学院，陕西 延安 716000)

高放废物处置库(以下简称处置库)开挖后，废物释热引起处置库近场围岩的热应力和应变影响围岩的稳定性,进而直接影响处置库后期安全运营和近场的核素迁移路径。开展热载作用下温度—应力—位移的岩体力学特性研究具有十分重要的理论意义和工程实用价值。

数十年来，处置库近场多场耦合问题的研究主要集中在数学解析分析和数值模拟分析方面。使用有限元和离散元模拟了spö柱稳定性实验过程的热—力(TM)耦合[1]。开展了裂隙花岗岩原型处置库的三维热—水—力耦合研究[2]。开展了热对黏土和花岗岩变形、应力和孔隙压力的影响研究[3]。探究了处置库单个竖直钻孔内废物包个数[4]，并未涉及单个竖直钻孔内废物包个数一定(每个钻孔放置1个废物罐)的条件下，研究多个竖直钻孔内废物包个数对处置库近场温度、应力和位移的影响。应用FLAC3D有限差分程序模拟计算了数百年内热—力耦合(TM)条件下处置库围岩的温度、应力和位移的变化特征[5]。开展了热—力耦合条件下处置室间距研究[6]。运用有限元软件Code-Bright对处置库关闭后处置库近场的温度场、渗流场、应力场进行了热—水—力耦合的数值模拟[7]。对单个废物罐周边的温度发展进行了热传导特性研究[8]。研究了中国地质处置库深度，通过处置库热学计算初步确定了处置间距和处置库规模[9]。开展了处置库热—力耦合数值模拟研究[10]。

值得指出，以上文献均未涉及废物罐数量(废物罐之间产生的热叠加效应)对处置库近场温度、应力、位移影响的复杂模型研究，而实际处置库近场温度、应力、位移与废物罐数量息息相关，不同废物罐数量对处置库近场温度场、应力场和位移场的影响直接关系到废物处置的安全和处置成本。基于此，开展高放废物处置多孔多罐热力耦合近场效应研究工作显得十分必要。本文首先采用3DEC离散元程序分别建立深地质处置库巷道内2个、3个、4个和5个废物罐模型；其次分别在巷道内设置2个、3个、4个和5个废物罐进行模型的温度、应力和位移计算；最后，由计算结果对比分析，揭示废物罐数量对处置库近场温度、应力、位移影响的规律。

1 概念模型

处置库概念模型如图1所示，概念处置深度为-500 m，处置区域设置1条巷道，巷道长分别为24 m(32 m、40 m和48 m)，巷道内分别设置2个、3个、4个和5个竖向钻孔，每个钻孔内放置1个废物罐，相邻废物罐中心间距均为8 m。废物罐周围设置0.5 m厚的膨润土，处置库围岩为花岗岩。

图1 处置库概念模型[11]Fig.1 The high-level radioactive waste repository concept model[11]

1.1 基本假定及其数学模型

模型计算假定：热传导发生在废物罐、膨润土和围岩中，文中分别定义其热物理参数。其数学模型如下。

(1)对于固体材料，热传导遵循傅里叶定律

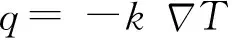
(1)

式中：q——材料的热流密度，W/m2；

k——材料的热传导系数，W·m-1·℃-1；

负号——热流方向与其温度梯度方向相反。

(2)热应力耦合

材料温度变化引起热应变，进而影响到应力；然而，热应力的计算不受力改变的影响。其热应力计算公式：

Δσij=-3KαtΔTδij

(2)

式中：Δσij——应力增量，Pa；

K——体积模量，Pa；

αt——线膨胀系数，1/℃；

δij——克罗内克张量，1，i=j；0，i≠j。

热应力以拉为正、压为负，温度以升高为正、降低为负。

1.2 算例模型

构建高放废物处置多孔多罐热力耦合的计算模型，本文算例模型尺寸为：24 m(32 m、40 m、48 m)[长]×10 m[宽]×20 m[高]，本文采用与文献[12]中圆柱体废物罐体积相等的原则换算成棱柱体，换算后单个废物罐的尺寸为0.8 m(长)×0.8 m(宽)×1.5 m(高)，周围设置500 mm厚的膨润土；对于燃耗为40 MW·d/kgU的乏燃料，后处理后制成玻璃固化体，并冷却30 a，每个废物罐剩余衰变热功率将为559 W[8]，本文模型中每个废物罐的热集度为582 W/m3。2个废物罐处置库的模型尺寸如图2所示(3个、4个和5个废物罐处置库的模型尺寸类同，文中未画出)，废物罐中心位于坐标(8 m、0.9 m、6.75 m)和(16 m、0.9 m、6.75 m)处，废物罐顶部距离巷道底部1 m处，废物罐中心距离巷道外侧(-y方向)0.9 m处。图2(a)为模型整体尺寸，(b)中A为外侧废物罐外表面膨润土(废物罐顶部以上0.5 m处)温度、应力和位移观察点；B、C为内侧废物罐外表面膨润土(废物罐顶部以上0.5 m处)温度、应力和位移观察点。2个废物罐处置库的数值模型网格划分如图3所示，为计算更加准确，废物罐处置区域及其外围岩区域采取三级网格划分加密处理。力学边界条件根据甘肃北山地区地质钻孔地应力测量结果，在-500 m处，地应力方向为NE，最大主应力为σH=15 MPa，σv=13 MPa，σh=10 MPa；热学边界条件为各侧面绝热。

图2 处置库的模型尺寸及观察点位置,mFig.2 Model size and observation point location of high-level radioactive waste repository,m

图3 模型网格划分Fig.3 Model mesh generation

1.3 参数与工况

根据北山地区花岗岩的热物理参数实测值，数值计算所采用花岗岩、膨润土与废物罐的热物理参数列于表1。在处置概念设计-500 m条件下的地温为19 ℃[9]。本文设定概念处置围岩类型为花岗岩，模型计算时设定废物罐、膨润土和花岗岩的初始温度为19 ℃。

表1 花岗岩、膨润土与废物罐的热物理参数[13]Table 1 Thermo-physical parameters of granite,bentonite and canister[13]

计算工况中，模型尺寸分别为：24 m(32 m、40 m、48 m[长]×10 m[宽]×20 m[高]，即处置库模型长度分别为24 m(模拟2个废物罐)、32 m(模拟3个废物罐)、40 m(模拟4个废物罐)和48 m(模拟5个废物罐)，宽度为10 m，高度为20 m，模拟热力耦合条件下处置库不同废物罐数量，计算分析热力耦合条件下废物罐数量对处置库近场温度、应力和位移影响的规律。数值模拟工况如表2所示。

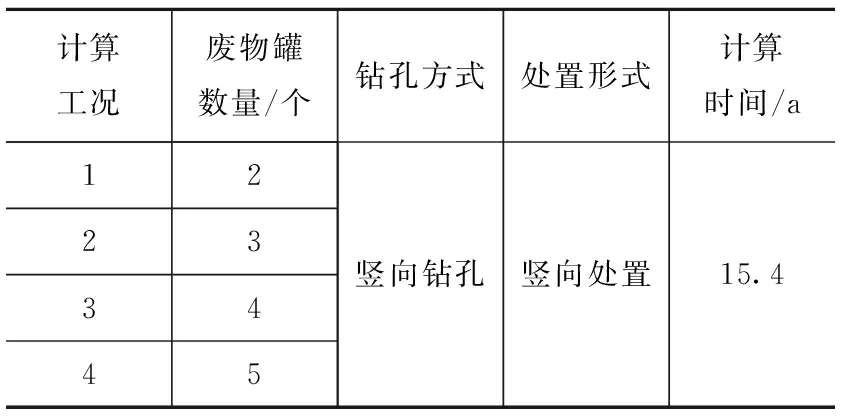
表2 数值模拟工况Table 2 Numerical simulation conditions

2 计算结果及对比分析

2.1 废物罐数量对处置库近场温度的影响

在2个、3个、4个和5个废物罐作用下，处置库近场瞬态温度场如图4所示。

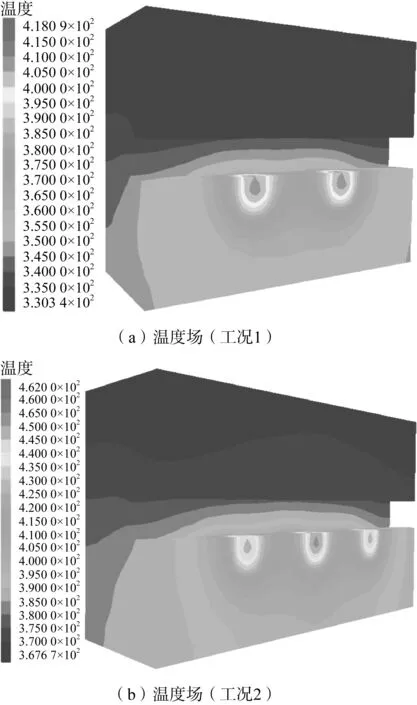
图4 处置库温度场,℃Fig.4 Temperature field of waste repository,℃

由图4可知，4个工况下处置库温度场等温线呈现出由废物罐群中心向其周边辐射的态势。由于存在巷道，并且废物罐设置于巷道底部使处置库下部温度高于其上部。在相同计算时间内，工况1的两个对称废物罐中央最高温度为418 ℃，围岩边缘最低温度为330 ℃，温度梯度为4.4 ℃/m，工况2的中央单个废物罐最高温度为462 ℃，边缘最低温度为368 ℃，温度梯度为4.7 ℃/m，工况3中部对称的两个废物罐最高温度为487 ℃，边缘最低温度为390 ℃，温度梯度为4.85 ℃/m，工况4的中央单个废物罐最高温度为504 ℃，边缘最低温度为403 ℃，温度梯度为5.05 ℃/m。究其原因，在绝热边界条件下，随着废物罐数量递增，废物罐释热必然增多，废物罐之间发生的热叠加效应进一步增强，必然导致其整体温度升高。每增加1个废物罐，岩体温度平均增幅约26.5 ℃，平均温度梯度增大约0.22 ℃/m。

在2个、3个、4个和5个废物罐作用下，废物罐表面膨润土时间-温度曲线如图5所示。

图5 废物罐表面膨润土时间-温度曲线 Fig.5 Time-temperature curve of bentonite on waste tank surface

由图5(a)知，在废物罐释热约0.6a时，4个工况下外侧废物罐表面膨润土观察点温度约100 ℃，其后观察点温度随时间呈线性分布，并且为5个废物罐时观察点最高温度约487 ℃，2个废物罐时观察点最低温度约411 ℃，原因同上。由图5(b)知，内侧膨润土观察点温度分布与外侧类似，并且为5个废物罐时观察点最高温度约496 ℃，3个废物罐时观察点最低温度约455 ℃。图5(a)与图5(b)对比知，同一工况下，内侧观察点温度高于外侧，原因同上。每增加1个废物罐，内侧比外侧观察点温度平均高约1.25 ℃，内侧观察点温度差值随时间小于其外侧。

2.2 废物罐数量对处置库近场位移的影响

在2个、3个、4个和5个废物罐作用下，处置库近场瞬态位移场如图6所示。

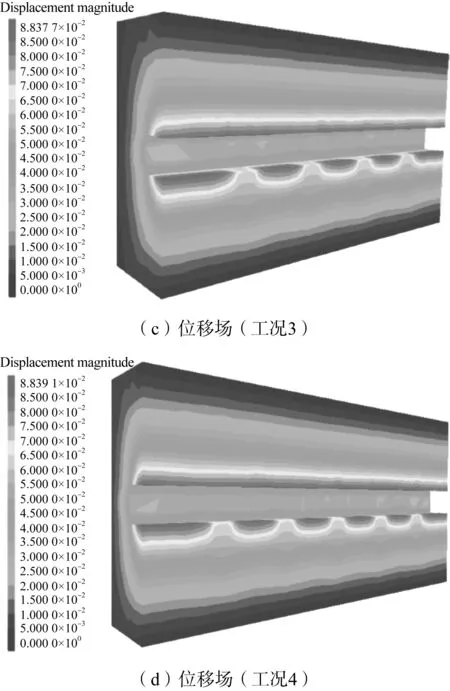
图6 处置库位移场,mFig.6 Displacement field of waste repository,m

由图6知，在2个、3个、4个和5个废物罐作用下，处置库位移场等势线均呈现出由巷道上、下部向周边辐射的态势。巷道上、下部位移最大，这是因为模型施加向下地应力的作用，巷道顶部无支撑作用(无向上作用力)，使巷道上部产生向下的位移，巷道下部均为废物罐之间热叠加效应区域产生的位移最大，这部分位移主要由热应力产生。在相同计算时间内，工况1的处置库最大位移为8.26 cm，工况2的处置库最大位移为8.66 cm，工况3的处置库最大位移为8.837 cm，工况4的处置库最大位移为8.839 cm，前三个工况，位移存在明显增幅。这是因为处置库的位移与其温度呈正相关，在原有应力产生的位移一定的条件下，热应力产生的位移必然进一步增大。每增加1个废物罐，岩体平均位移增幅约0.193 cm，处置库近场相同位置区域位移随废物罐数量增多而逐渐增大。

在2个、3个、4个和5个废物罐作用下，废物罐表面膨润土时间—竖向位移曲线如图7所示。

图7 废物罐表面膨润土时间—竖向位移曲线Fig.7 Time-vertical displacement curve of bentonite on waste tank surface

由图7(a)知，在废物罐释热0～0.6 a 时，4个工况下外侧废物罐表面膨润土观察点竖向位移随时间增幅较大，位移达到3.9 cm，其后观察点位移随时间增幅较小，呈线性分布，并且为5个废物罐时观察点最大位移约6.2 cm，2个废物罐时观察点最小位移约5.76 cm。由图7(b)知，内侧观察点竖向位移分布与其外侧类似，并且为5个废物罐时观察点最大位移约6.3 cm，3个废物罐时观察点最小位移约5.98 cm。图7(a)与图7(b)对比知，同一工况下，内侧观察点位移大于外侧，这是由于内侧废物罐释热后热量叠加效应更强，进而产生更大位移的缘故。结合图5知，这与相同观察点温度呈正相关，即观察点竖向位移随着温度升高而增大，这是由于废物罐释热初期地应力作用比较明显，随着废物罐释热时间，巷道顶部出现竖直向上的热应力，这必然会使巷道顶部观察点位移不断增大，这是热应力与地应力共同作用的结果。内侧观察点温度差值随时间小于其外侧。

2.3 废物罐数量对处置库近场应力的影响

在2个、3个、4个和5个废物罐作用下，不同观察点时间-竖向应力曲线如图8所示。

图8 废物罐表面膨润土时间—竖向应力曲线Fig.8 Time-vertical stress curve of bentonite on waste tank surface

由图8知，由于施加初始竖向压应力13 MPa，在废物罐释热约0.6 a时，工况1中观察点A的拉应力最小，工况4中观察点A的拉应力最大。在废物罐释热约0～0.6 a时，4个工况下，外侧废物罐表面膨润土观察点竖向应力增幅较大，由初始施加的地应力转变为热量产生的向上的热拉应力，并且应力达到2～2.8 MPa。这与温度图5和图7废物罐表面膨润土时间—温度(位移)曲线规律有类似特点。0.6 a后观察点应力增大随时间增幅较小，基本保持不变或略有减小。这主要是由于废物罐释热初期地应力(施加于模型向下的应力)作用比较明显，随着废物罐释热时间，巷道顶部出现向上的热应力，这必然会使初始压应力减小一部分，出现由压应力转变为向上的热拉应力。另外，内侧观察点竖向应力差值随时间小于其外侧。

综合以上可知，工程设计中增加的废物罐数量产生的热叠加效应不容忽视，建议单个钻孔内处置1个废物罐为宜。

3 结论

(1)每增加1个废物罐，岩体平均温度升高约26.5 ℃，平均温度梯度增大约0.22 ℃/m，内侧比外侧观察点平均温度高约1.25 ℃，岩体平均位移增大约0.193 cm，并且内侧观察点温度、位移和应力差值随时间小于其外侧。

(2)废物罐释热0～0.6 a时，膨润土的温度、竖向位移和竖向应力增幅较大，其后膨润土温度和竖向位移增幅减小，由初始施加的地应力变为温度产生的2～2.8 MPa的热拉应力，膨润土竖向应力随时间基本保持不变或略有减小。

(3)工程设计中增加的废物罐数量产生的热叠加效应不容忽视，建议单个钻孔内处置1个废物罐为宜。