压力铸造成型工艺参数优化数学模型研究

赵 瑜

(江苏信息职业技术学院 基础课部，江苏 无锡 214153)

0 引言

压铸成型是一种利用高压强制将金属熔液压入形状复杂的金属模具内的一种先进的精致铸造法[1]，其被广泛于机械、电子、轻工、国防等领域，压铸成型主要包括压铸模、压铸设备和压铸工艺3大要素[2]。压铸成型工艺参数的选择对铸件成型质量有着直接的影响[3]。在成型过程，模具的失效70%是由热疲劳导引起[4]，因此，为解决压铸成型工艺参数对模具热疲劳的影响，降低集中热应力，本文提出了一种基于代理模型的方法来建立压铸成型工艺参数与铸件模具热应力之间的关系；常用的代理模型有Kriging[5]，响应面[6]、神经网络[7]，支持向量机[8]等， 本文采用Kriging算法建立压铸成型工艺参数与模具热疲劳应力之间的数学模型，同时为提高Kriging代理模型的精度，采用量子粒子群算法对Kriging代理模型的变差函数的参数进行优化，提高Kriging建立压铸成型工艺参数与模具热应力之间数学模型精度，从而为压铸成型工艺参数优化提供更加精确的数学模型，基于建立的数学模型可采用相应的智能优化算法对其优化，实现压铸成型工艺参数与热应力之间的最佳匹配；降低热应，延长模具寿命，提高零件的成形质量。

1 克里金代理模型

Kriging模型处理非线性拟合问题时，可较容易获得理想的拟合结果。Kriging将拟拟合函数视为是某个静态随机过程的具体实现，即对于任意位置的x，对应的函数值Y(x)被一个随机函数y(x)代替，而y(x)只是Y(x)的可能结果之一。其插值结果为已知样本函数响应值的线性加权，即：

(1)

式中：fj(x) ——函数(多项式)；βj——相对应的系数；Z(x) ——静态随机过程，其满足均值为0，方差为σ2。

设计空间内不同两点处所对应的随机变量间的协方差定义如下：

Cov[Z(xi)，Z(xj)]=σ2R(xi，xj)

(2)

(3)

式中：R(xi，xj) ——相关性函数，它表针不同位置处随机变量之间的相关性，常用的相关性函数为高斯型函数。

Kriging预测模型的近似表达式为：

(4)

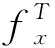
式(3)中的θ为Kriging模型的超参数，它可以通过极大似然估计法求解优化问题来确定：

(5)

2 试验设计及响应

2.1 铝合金压铸成型工艺参数及水平

参考文献[4]，以采用AL365材料压铸的咖啡机顶盖为列，研究铝合金压铸浇注温度 、模具温度 、充填速度和压射比压成型工艺参数对模具热应力的影响，工艺参数(浇注温度、模具温度、充填速度和压射比压)的取值范围及其水平(每个因素取4水平)如表1所示。

表1 铝合金压铸成型工艺参数范围与水平表

2.2 试验设计及其响应

参考文献[4]，本文采用正交试验对表1中进行试验设计，正交试验设计及响应如表2、表3所示，其中，表2用于训练Kriging模型，用于测试建立的模型的精度。

表2 正交试验及其响应(训练集)

表2(续)

表3 正交试验及其响应(测试集)

3 基于QPSO算法的预测模型改进

标准粒子群算法粒子的速度和位置更新公式为：

Vi，j(t+1)=w(t)Vi，j(t)+c1r1[Pi，j(t)-Xi，j(t)]+c2r2[Pg，j(t)-Xi，j(t)]

(6)

Xi，j(t+1)=Xi，j(t)+Vi，j(t+1)

(7)

上式中，*i，j(t)，*=V，P，X等表示第t次迭代粒子i第j维*分量；c1，c2为加速度常数，用于调整学习步长，r1，r2为[0，1]之间的随机数。Vi，j一般在限制在[Xmin，Xmax]。

令φi，j(t)=c1(t)r1，j(t)/[c1(t)r1，j(t)+c2(t)r2，j(t))]，取c1=c2，因此有φi，j(t)～U(0，1)，1≤j≤N，则粒子收敛时以点pi(t)=(pi，l(t)，pi，2(t)，…，pi，N(t))为吸引且pi(t)为Pbest和gbest间的随机值，其表达式为：

Pi，j(t)=φi，j(t)Pi，j(t)+(1-φi，j(t))Pi，j(t)

(8)

在迭代过程中，粒子不断的靠近并最终到达点pi。因此，在迭代过程时，如果存在着一种势能(吸引势)在引导粒子向着pi点靠近，从而保证了整个粒子群体的聚集性，而不会趋向无穷大。

具有量子行为的粒子群算法的位置更新方程表达式为：

(9)

本文中采用Li，j(t)=2α|Cj(t)-Xi，j(t)，α为扩张—收缩因子，QPSO方程可转换为：

Xi，j(t+1)=pi，j(t)±α|Cj(t)-Xi，j(t)|ln(1/ui，j(t))，ui，j(t)～U(0，1)

(10)

pi，j(t)=Pg，j(t)+φi，j(t)[Pi，j(t)-Pg，j(t)]

(11)

(12)

4 数值仿真

利用MATLAB数字仿真软件，分别利用Kriging和基于QPSO算法改进的kriging算法建立压铸成型模具热疲劳应力预测模型，优化前后的相关系数(R2)均方根误差(RMSE)以及相对最大绝对误差(RMAE)评价指标情况如表4所示。

表4 优化前后评价指标情况

从表4中可以看出，本文所提出的基于量子粒子群算法改进Kriging算法后，Kriging代理模型精度评价指标R2提高了9.4741%，越接近于1全局近似能力提升，RMSE降低了82.3207%，接近于0，预测值与真实值之间的偏离程度越小，RMAE降低了84.9139%，减少了模型的局部误差；综合来看，采用基于量子粒子群算法改进Kriging算法，提升了Kriging算法的拟合能力和精度。

利用Kriging和基于量子粒子群算法改进Kriging算法建立的工艺参数与控制量之间的预测模型预测结果分别如图1、图2所示，预测残差图如图3、图4所示。

图1 基于Kriging模型的预测结果 图2 基于QPSO-Kriging模型的预测结果

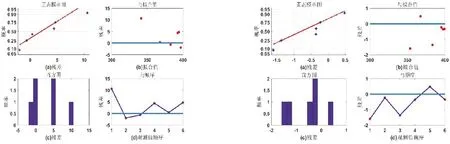
图3 基于Kriging模型的预测残差图 图4 基于QPSO-Kriging模型的预测残差图

从图1-图4可以看出，改进后的Kriging模型的预测误差更小，由原来的[-2，10]优化为[-2，1]之间，提高了Kriging模型的拟合精度，建立了压铸工艺参数与控制量之间的更加精确数学模型，为工艺参数优化提供更加准确的数学模型。

5 结论

本文针对压铸成型的工艺参数系统难以建立精确的数学模型的问题，本文提出了一种基于量子粒子群算法改进的Kriging算法，用于建立压铸成型工艺参数与压铸成型模具热疲劳应力之间的数学模型。

(1)基于量子粒子群算法改进Kriging算法后，Kriging代理模型精度评价指标R2提高了9.4741%，越接近于1全局近似能力提升，RMSE降低了82.3207%，接近于0，预测值与真实值之间的偏离程度越小，RMAE降低了84.9139%，减少了模型的局部误差。

(2)改进后的Kriging模型的预测误差更小，由原来的[-2，10]优化为[-2，1]之间，提高了Kriging模型的拟合精度，建立了压铸工艺参数与压铸成型模具热疲劳应力之间的更加精确数学模型。