空间充气杆件及挂帆展开过程分析

2020-10-13赵巨岩赵海燕

导弹与航天运载技术 2020年5期

束逸，赵巨岩，赵海燕

（1. 北京航天长征飞行器研究所，北京，100072；2. 清华大学机械工程系，北京，100084）

0 引言

空间可展开结构由于其具有折叠尺寸小、质量轻、展开结构设计自由度大等优势被越来越多地应用在空间结构领域。尤其是在大型空间结构设计方面，折叠展开方案具有突出的技术优势和成本优势，成为许多大型空间结构为数不多的技术解决方案之一[1～3]。

在多种可展开结构设计方案中，充气可展开结构由于采用了柔性充气囊体作为主要的结构支撑件，具有如下优势：a）可突破机械式展开结构的尺寸限制，实现超大型空间结构；b）材料和结构具有良好的可设计性，可以通过优化组分材料的比例、调整充气压力等方式达到结构体系所要求的刚度、强度等指标；c）结构简单、研制费用低；d）发射体积小、质量轻、包装形状灵活，能有效提高发射装载空间的利用效率。

然而，由于空间充气结构的主体材料—薄膜材料的柔性性质，使得结构的折叠和展开具有较大的不确定性。尤其是大型充气展开结构，复杂的折叠方式和结构在展开过程中可能会发生卡顿、阻滞、甚至交叉缠绕的现象。由此带来的充气结构展开可靠性问题对于高成本高风险的航天应用来说是不可接受的。为了更好地指导空间充气结构的展开设计，缩短样机研制的迭代周期，研制出高可靠性空间充气展开结构，有必要进行空间充气结构折叠展开过程的数值分析[4,5]。

本文针对多边形折叠的充气杆件以及与之配套的帆面组成的整体空间充气展开结构进行数值仿真分析，对折叠形式进行了优化，对展开过程进行了验证。

1 单充气杆折叠模型建立

通常情况下，充气杆为薄膜材料热合形成的管状结构，为了保证该管状结构折叠紧凑性以及展开过程的平顺性，将充气管折叠成风箱结构，通常有四边形、六边形及八边形折叠方式，其折叠折痕如图1 所示。

图1 四边、六边及八边形充气杆折痕Fig.1 Quadrangle, Hexagonal and Octagonal Creases of the Inflatable Beam

目前已有相关文献研究了采用这种折叠结构的充气杆件在航天器机构中应用[6～8]，但仍处于研发阶段，结构在展开和折叠状态下具有大体积比。在该仿真分析中，由于相等展开横截面下的四边形折叠方式的折叠体积不满足要求，因此以六边形折叠和八边形折叠的充气杆件为研究对象进行建模。

在ANSYS Multiphysics/LS-DYNA 环境下进行基本模型的建立，如图2 所示。

图2 六边形及八边形充气杆折叠模型（局部）Fig.2 Folding Inflatable Beam Model (Local)

如图2 所示，六边形及八边形折叠形式具有轴向周期性，分析一个周期内折叠划片形式，可知各关键角点都是分两层分布在正六/八边形上。因此，采取由点到面，由单周期到多周期的建模方式，建立充气杆囊体的模型。通常情况下，充气杆端头部位为圆形端盖，在总体折叠模型建立后还需建立圆形端盖以及其过渡结构。建模参数见表1。

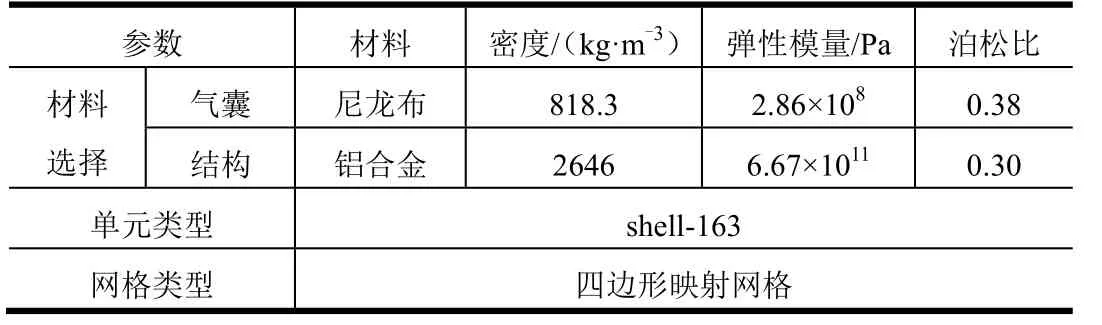
表1 建模参数Tab.1 Air-inflation Initial Segment Loading Parameters

采用上述网格类型的充气杆件后对充气杆模型进行网格划分，划分后结果如图3 所示。

图3 八边形折叠充气杆网格划分模型Fig.3 Folding Octagonal Inflatable Beam Mesh Model

2 单充气杆展开过程模拟

在ANSYS 中完成折叠充气杆件的模型建立和网格划分后生成的k 文件，在LS-DYNA Solver 中进行充气的仿真。仿真中充气杆采用的气囊材料模型为*MAT_FABRIC （织物），气囊模型为*AIRBAG_SIMPLE_AIRBAG_MODEL（气流充气模型）。

通过分析计算得到了六边形以及八边形折叠充气杆件的展开过程结果，如图4、5 所示。

图4 六边形折叠充气杆件展开过程分析结果Fig.4 Analysis Results of Expansion Process of the Folded Hexagonal Inflatable Beam

图5 八边形折叠充气杆件展开过程分析结果Fig.5 Analysis Results of Expansion Process of the Folded Octagonal Inflatable Beam

由图4、图5 可知，六边形及八边形折叠充气杆的展开过程分析中两类充气杆件都可按照既定方向和形式展开。为了分析两类杆件的展开过程的稳定性和可靠性，基于上述仿真结果进行充气杆囊体体积及内压力分析，获取充气过程中充气杆体积随时间的膨胀关系，压力随时间的关系。

图6 和图7 为八边形折叠和六边形折叠充气杆充气过程囊体体积膨胀过程。从图中分析可知，整个过程大致分为：折叠展开成形阶段和薄膜应变膨胀阶段。在两个状态转换、充气杆展开成形刚结束阶段，会发生囊体弹性抖动问题，抖动会持续一段时间，直至能量耗散结束。这一抖动对整个充气结构的展开是不利的，因此需要尽量消除。

由图6 和图7 可知，八边形折叠充气杆件展开过程较六边形折叠杆件具有更长的体积抖动弛豫时间，而两者的最大抖动幅度基本一致。

图6 八边形充气杆充气展开过程体积-时间关系Fig.6 Volume-time Curve of the Octagonal Beam Expnsion Process

图7 六边形充气杆充气展开过程体积-时间关系Fig.7 Volume-time Curve of the Hexagonal Beam Expnsion Process

图8 和图9 为不同折叠方式充气杆内压强与时间的关系，从图中曲线可知，八边形折叠的充气杆展开过程中气压同样存在波动。为了保证充气杆件展开过程的稳定性和流畅性，六边形折叠充气杆更具优势。

图8 八边形充气杆充气展开过程气压-时间关系Fig.8 Pressure-time Curve of the Octagonal Beam Expnsion Process

图9 六边形充气杆充气展开过程气压-时间关系Fig.9 Pressure-time Curve of the Hexagonal Beam Expnsion Process

3 单充气杆展开气流稳定性

复杂的空间充气可展开结构通常由多个上述的充气杆件组成，结构中还同时包含其它被动折叠展开组件（如展开帆面）及刚性负载。因此，要实现整个结构和流畅可控展开成形，就不得不考虑各展开部件展开过程的同步性问题。对于各展开充气杆件来说，充气气流的不稳定是造成展开同步性最关键因素。为考察不同折叠形式充气杆件对不稳定气流的响应，进行气流稳定性仿真分析结果如图10、11 所示。考虑到不稳定气流的极端情况，即充气过程突然停止，在仿真加载中设定。理想情况下，充气杆停止充气，杆件体积就不再增加。然而，从图10 和图11 分析结果可知，充气杆体积在充气停止后同样存在抖动现象，对于八边形充气杆件，体积抖动一直延续到0.1 s，而六边形充气杆件则仅存在0.01 s 的体积抖动。在充气气流不稳定的情况下，八边形的充气杆件的展开过程更易受到影响。

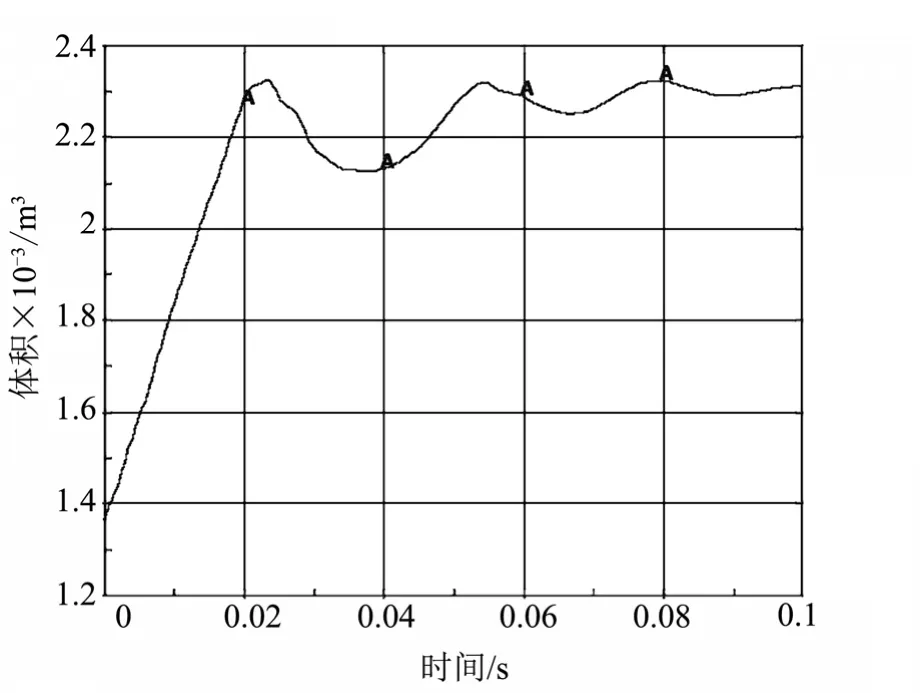
图10 八边形充气杆展开过程（中断）体积-时间关系Fig.10 Volume-time Curve of the Octagonal Beam Expnsion and Termination

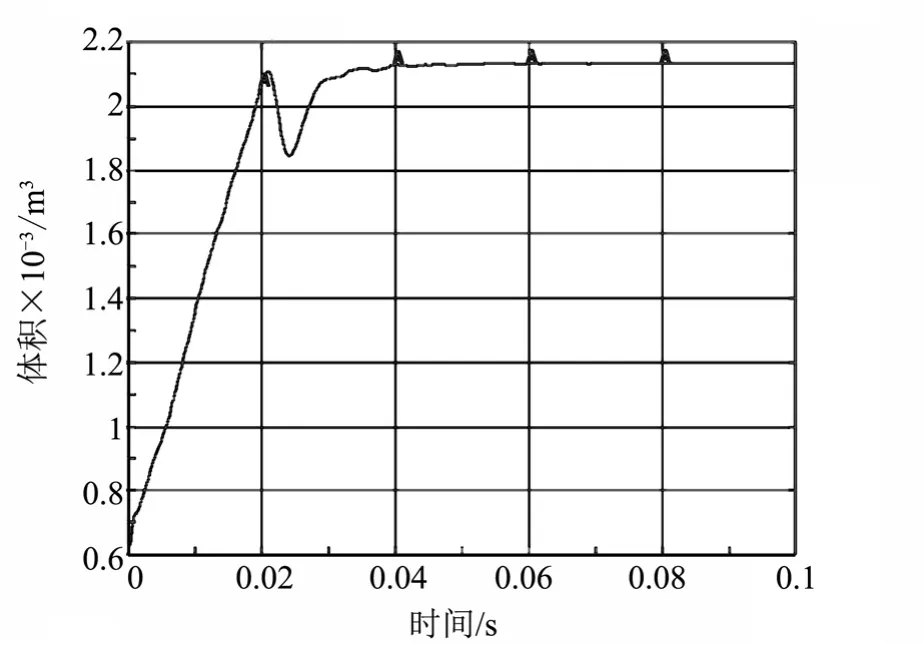
图11 六边形充气杆展开过程（中断）体积-时间关系Fig.11 Volume-time Curve of the Hexagonal Beam Expnsion and Termination

图12、13 为两种折叠杆件的展开过程压力-时间曲线，与体积变化的情况类似，八边形折叠充气杆件的压力波动持续到展开后0.08 s，而六边形杆件的压力波动则仅持续了0.01 s。

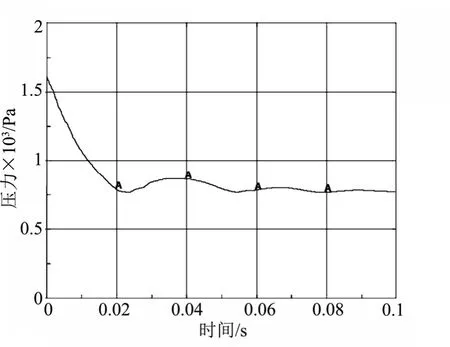
图12 八边形充气杆展开过程（中断）压力-时间关系Fig.12 Pressure-time Curve of the Octagonal Beam Expnsion and Termination

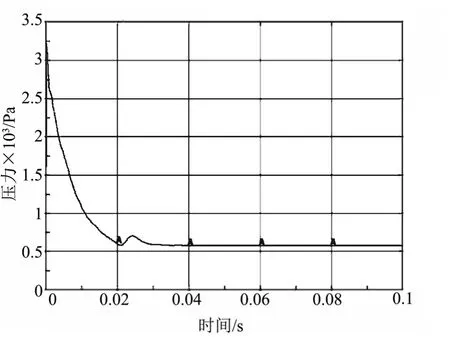
图13 六边形充气杆展开过程（中断）压力-时间关系Fig.13 Pressure-time Curve of the Hexagonal Beam Expnsion and Termination

由上述分析可知，在全过程的展开分析和充气中止的展开分析中，六边形折叠的充气杆件相较于八边形充气杆件具有更加稳定的体积和气压变化过程。这一趋势可定性解释为：八边形折叠较六边形折叠具有更好的趋圆性，在充气过程中，折叠囊片更易于展开张紧，而张紧囊片的弹性振动是形成气压和体积抖动的主要原因。这一特性对于由该类充气杆件组成的空间充气展开结构而言具有稳定性和可靠性优势，因此在后续分析中主要采用六边形折叠的充气杆件模型，分析复杂充气结构展开流畅性。

4 杆帆复合结构展开仿真计算

在完成单根折叠充气杆件的仿真计算后，进行了基本的充气复合结构的分析计算。在计算模型中，将两个六边形折叠充气杆相互正交排布，两充气杆皆为一端固定且固定端相邻。折叠的直角三角形帆面挂载于充气杆上随杆一同展开，帆面直角端点固定在充气杆底部，另外两端点固定与充气杆活动端。

帆布折叠的方式如图14 所示，将帆布以两个直角边为基线按扇子状折叠，由二维面折叠成一维条状，再将条状折叠帆中的3 个角点挂于相应锚点处。复合结构的有限元模型如图15 所示。两个充气管外面各包络有一层壳壁，作用分别为：a）限制该段充气管的轴向膨胀，使之尽可能沿轴向膨胀运动；b）为帆布的悬挂提供位点。

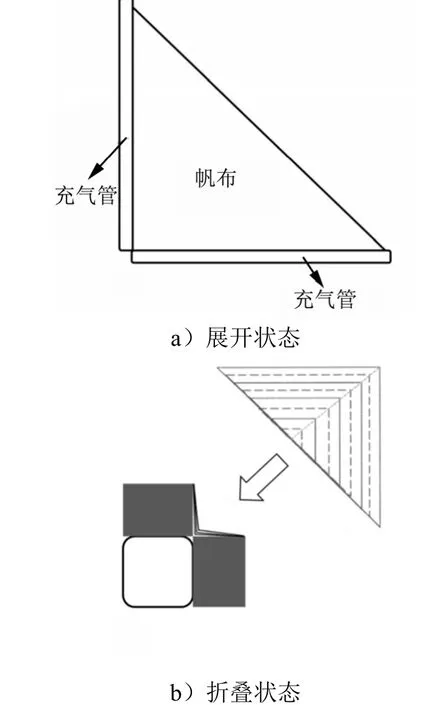
图14 充气复合结构Fig.14 Inflatable Composite Structure

图15 充气管挂帆简化充气展开装置的有限元模型充气杆-帆面复合结构Fig.15 The FEA Model of the Simplified Appliance Including Two Orthogonal Placed Beams with Sail

真实充气结构中，充气杆外挂帆面通常为对称形式，仿真中为了简化模型和计算量而采用双杆单帆面形式，因此充气杆还加载了对称约束。

充气杆-帆面复合结构充气展开过程的模拟结果如图16 所示，帆面能够顺利跟随充气杆件展开，初步验证了充气杆帆面复合结构的可行性。

图16 充气杆-帆面复合结构充气展开过程模拟结果Fig.16 Expansion Process Simulation Results

图17为充气杆帆面复合结构展开过程中的体积和气压时间曲线。

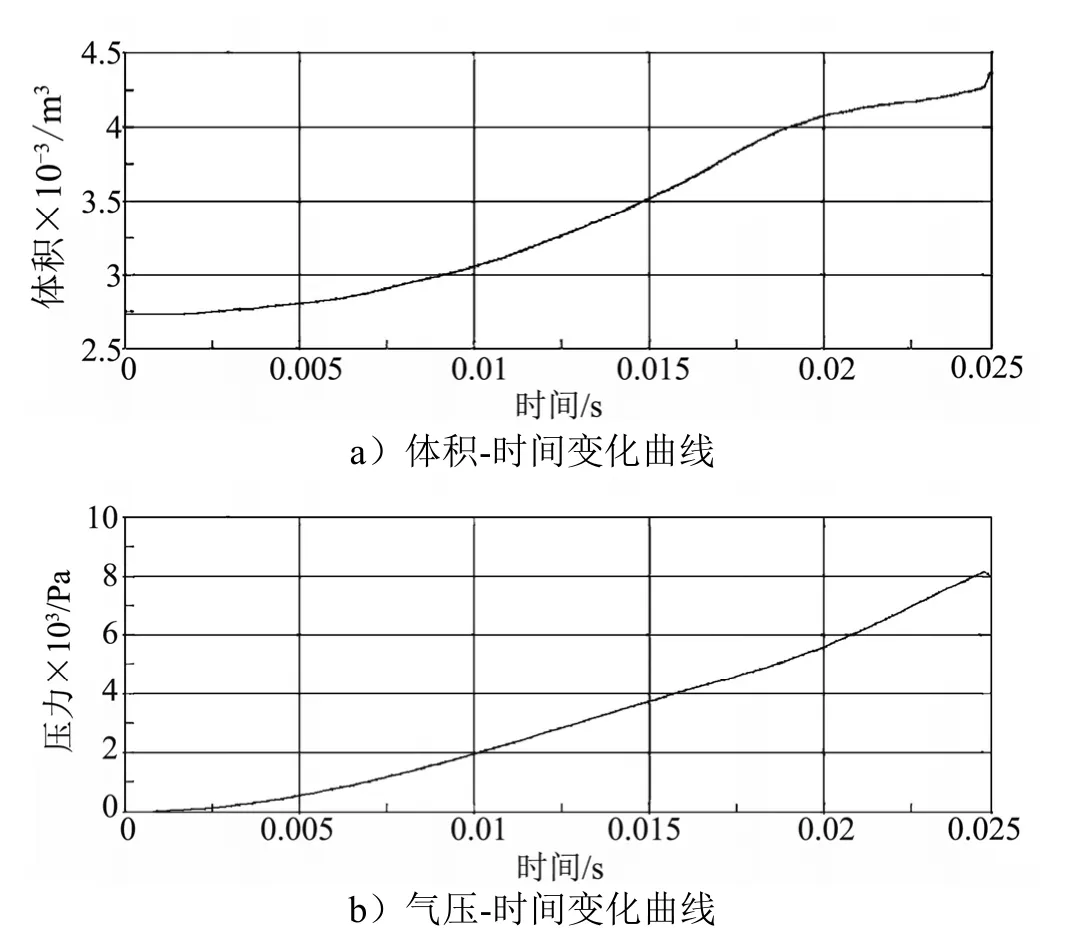
图17 复合结构的展开过程分析结果Fig.17 Composite Structure Simulation Results

由图7a 可以看出，整个装置内部体积变化曲线平滑，说明展开比较顺利，在结尾处稍有一个小尖峰，原因可能在于最后阶段帆布的直角边基本绷紧，对充气管的进一步体积变化产生一定的影响。图7b 与图7a的曲线相似，也说明充气管能保持柔性和平滑的展开，说明该装置采用多边形折叠充气管和挂帆的复合结构展开方式具有一定的可行性。