冲击载荷下多孔涂层材料建模与典型结构计算

赵巨岩，孟 刚，赵海燕，王道荣2,

（1. 清华大学力学与机械工程系，北京，100084；2. 北京航天长征飞行器研究所，北京，100076；3. 试验物理与计算数学国家级重点实验室，北京，100076）

0 引 言

多孔涂层材料由于制备工艺简单、密度小、成本低、工期短，特别是孔隙度易调节、吸能耗波以及耐高温性能好等优势，广泛应用于汽车、船舶、航空、航天等领域。通常与合金材料配合应用，由于工艺不同而对脉冲载荷的衰减作用具有不确定性。Katsube等[1]对多孔涂层材料的本构关系进行研究，Lizuka 等[2]对多孔涂层材料在高温下的力学性能参数进行研究。但迄今为止，尚缺乏对其动态力学参数的试验测量结果，更缺乏对其动态力学性能的系统试验和理论研究结果。

在工程实践中，多孔涂层材料作为功能材料已在众多领域中得到广泛应用。目前多孔涂层材料由于其微结构的多样性，具有相当优异的力学特性和能量吸收能力。多孔涂层材料的静态或准静态的力学特性研究的较为系统，多孔材料的动态力学响应研究较少。本文针对多孔涂层材料不同应变率效应下材料的特点，建立了多孔涂层材料的等效模型，研究多孔材料对脉冲载荷的衰减特性，为结构防护提供一种理论设计方法和效果分析途径。

1 动态应力-应变关系试验研究

1.1 SHPB 试验

分离式霍普金森（Split Hopkinson Pressure Bar，SHPB）装置测试系统如图1 所示。当撞击杆以某一速度撞击输入杆时，在杆内产生一个入射脉冲 εi，试件在该应力脉冲作用下产生高速变形，与此同时，在输入输出杆中分别产生反射脉冲 εr和透射脉冲 εt。在一维应力假定（又称平面假定）的基础上，可直接利用一维应力波理论确定应变率 ε˙( t) 、应变 ε( t) 和应力 σ( t) ：

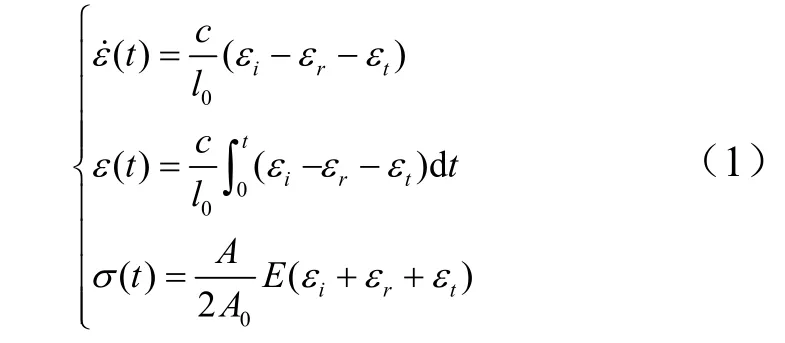
式中l0为试件初始的长度；c 为波速；A 为试件在应力脉冲作用下产生变形后的截面积； A0为试件初始的截面积；E 为杨氏模量。

图1 SHPB 装置Fig.1 SHPB Equipment

采用解耦法对数据进行处理得出等应变率应力-应变曲线，如图2 所示，曲线开始为单调上升的加载段，到A 点材料破裂，曲线下落，随着破裂的材料不断被压实，曲线到B 点后重新上升。图3 为冲击加载下不同应变率时材料应力-应变曲线的比较。

图2 冲击加载全过程曲线Fig.2 Whole Process Curve of Impact Loading

图3 冲击加载下不同应变率材料应力-应变曲线Fig.3 Comparison of Stress-strain Curves of Materials with Different Strain Rates under Impact Loading

1.2 材料性能的应变率效应分析

将进行静态试验得到的较低应变率加载与冲击加载的不同应变率下材料应力-应变曲线组合在一起，如图4 所示。

图4 不同应变率下材料应力-应变曲线Fig.4 Comparison of Stress-strain Curves of Materials with Different Strain Rates

由图4 可以看出，应变率对应力-应变关系的影响是显著的。可以得出以下分析结果：

a）多孔涂层材料的本构关系和力学性能有着明显的应变率正敏感效应：随着应变率的提高其整个应力应变曲线明显上移；材料的屈服应力和破坏应力都有明显提高；高应变率下的冲击破坏应变（<10%）明显小于其低应变率下的准静态破坏应变（>40%），相对于低应变率下的准静态加载，材料在冲击条件下显现出较明显的脆性特征。

b）材料在准静态加载的较低应变率范围内（ε˙＜10-1/s）的应力-应变曲线具有大多数多孔材料力学性能的基本特征，经历3 个典型的阶段：第1 阶段是弹性变形阶段，包括起初的较长直线段和极短暂的非线性弹性变形阶段，这阶段主要反映了材料骨料的承载和变形的特征；第2 阶段是很长的有微弱硬化趋势的近似屈服平台区，这阶段主要反映了骨料结构的被压垮和孔隙缩陷特征；第3 阶段是较明显增强的加强硬化阶段，这阶段反映出孔隙压实后整个压实材料的抗压特性，直至整个材料被破坏。第2 阶段和第3 阶段很长，材料可以有高达40%～50%的破坏应变，使得多孔涂层材料在较低应变率下有很好的吸能耗能效应。

c）在冲击加载的高应变率范围内，多孔涂层材料的应力-应变曲线表现出与低应变率下的二维静态应力-应变曲线显著不同的特征，没有明显的线弹性变形阶段和很长时间的近似屈服平台阶段，材料脆性增强，在比低应变率下破坏应变小许多的动态破坏应变之下即出现破坏，而其应力-应变曲线的性质类似于许多高分子材料非线性粘弹性应力-应变曲线的特征，这表明可采用改进型ZWT 本构模型对其本构行为进行拟合。

2 本构模型拟合

ZWT 本构模型源于对典型工程塑料，如环氧树脂、有机玻璃PMMA、聚碳酸脂PC、尼龙等材料，用于进行本构模型的拟合，结合试验结果发现该模型同样适用于高聚物复合材料，可用于脆性多孔涂层材料的本构模型拟合。

根据本次试验数据，对原模型进行适当的改进，得到改进型ZWT 本构方程：

式中ε0˙为参考应变率，取 ε0˙=1/s；E0，E1，E2，E3，α，n 和m 为需要拟合的参数，其中E0，E1，E2，E3具有应力的量纲，α，n 和m 为无量纲参数。

根据试验数据拟合得出：E0=-16.06 MPa；E1=105.85 MPa；E2=-33.96 MPa；E3=28.015 MPa；α=0.0222；n=0.103；m=0.0304。

为了更清楚地给出试验曲线和拟合曲线的关系，图5 为冲击加载情况下的试验和改进型ZWT 本构方程拟合结果对比。

图5 冲击加载本构关系的改进ZWT 模型拟合结果Fig.5 The Improved ZWT Model Fitting Results of Impact Loading Constitutive Relation

为了便于选择和比较，对于冲击（高应变率）加载的情况，还选用了著名的Bodner-Partom 粘塑性模型对试验数据进行拟合，Bodner-Partom 模型形式如下：

式中σ0，A，B，m 为需要通过试验获得的参数。

根据试验数据拟合所出：σ0＝1865.0MPa；A＝-13.0；B＝67.4；m＝0.177； ε0˙=2160/s。

图6 为冲击加载情况下的试验和Bodner-Partom 模型本构方程拟合结果对比。

图6 冲击加载本构关系的Bodner-Partom 模型拟合结果Fig.6 The Bodner-Partom Model Fitting Results of Impact Loading Constitutive Relation

3 典型圆筒结构动态响应数值模拟研究

3.1 计算模型

针对涂层材料的特点，在复合材料损伤破坏模型的基础上，建立了涂层材料等效力学模型，并针对两种模型进行了数值模拟的对比，两种模型的数值模拟结果都与试验结果有很好的一致性。同时采用非线性显式有限元软件研究某圆筒结构分别在有涂层和无涂层材料的防护情况下筒状壳体在冲击载荷下的的结构瞬时动力响应，从而考察多孔涂层材料的缓冲性能。这对于改进某装置壳体结构设计和完善材料性能具有重要的工程价值。

物理模型是轴对称的，载荷是面对称的，因此可只建立模型1/2，图7 给出了某圆筒结构的剖面形式，除两端的盖板外，中间有加强肋板，圆筒壳体的材料为铸铝。带多孔涂层防护层的有限元模型如图8 所示，圆筒结构处于自由状态，不定义空间约束条件，但是必须在模型的两个对称面上施加对称边界约束。

图7 圆筒有限元模型Fig.7 Finite Element Model of Unprotected Cylinder

图8 带多孔涂层圆筒有限元模型Fig.8 Finite Element Model of Porous Coated Cylinder

假设受到峰值为GPa 量级的脉冲，持续时间1 µs，面载荷的空间分布如图9 所示。施加的载荷模型如图10 所示。

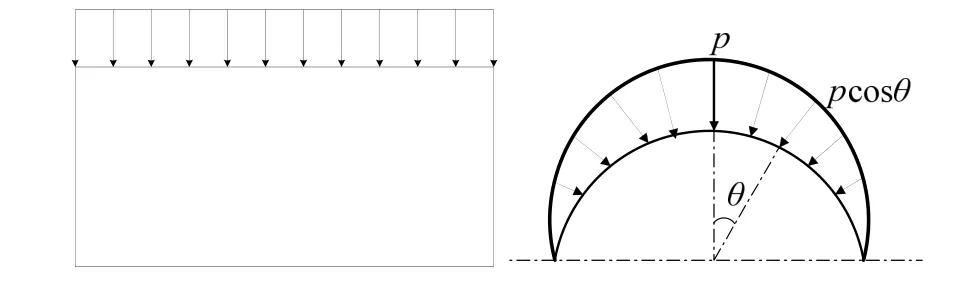
图9 简化载荷的空间余弦分布Fig.9 Spatial Distribution of Load

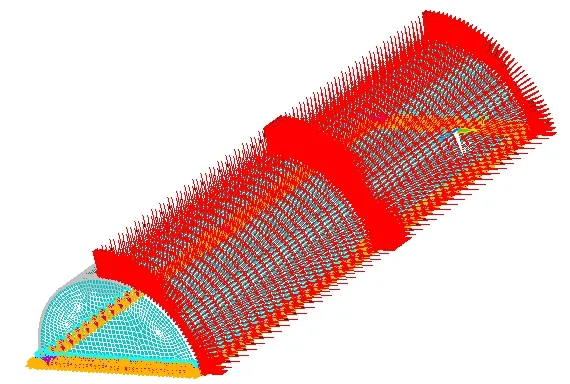
图10 施加载荷模型Fig.10 Model of Loading

3.2 无涂层圆筒结构响应数值分析

图11 给出不同时刻模型的等效应力云图。圆筒结构在1.39×10-5s 之后发生破裂、断裂；在4.7×10-4s 时破裂达到最大程度，不再继续扩展，此后的应力值一直在屈服应力左右发生振荡。

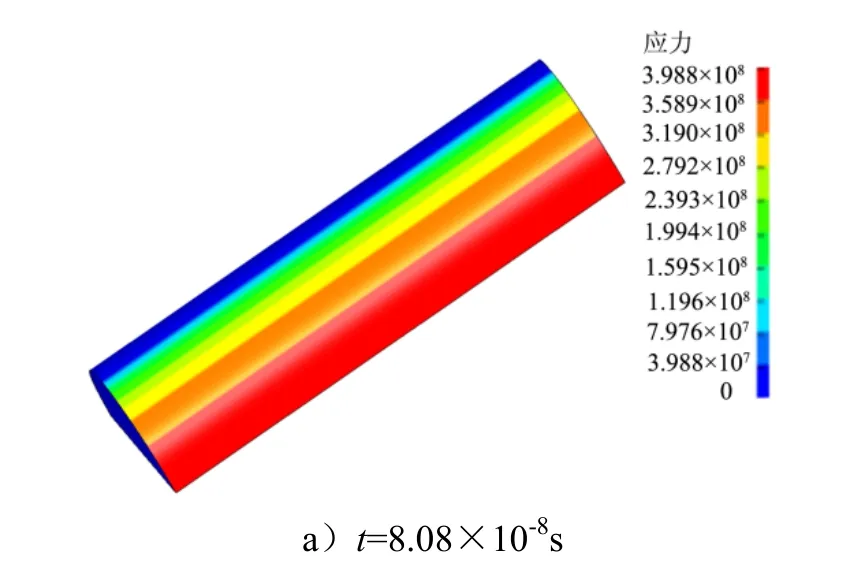
图11 不同时刻模型的等效应力云图Fig.11 Contours of Effective Stress of Model at Different Time

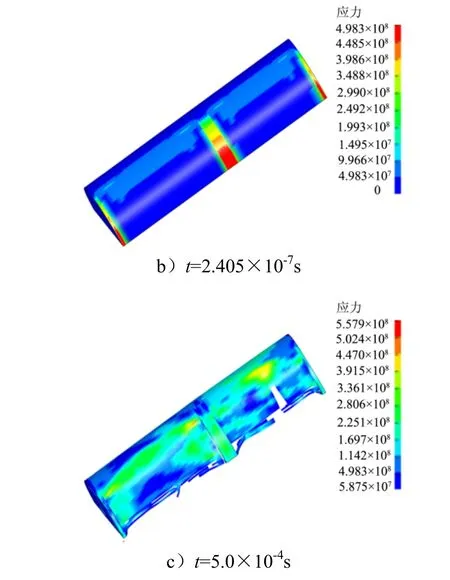
续图11

由图11 可知，圆筒发生了结构变形、断裂和弹塑性应变破坏。

3.3 包裹多孔涂层圆筒结构响应数值分析

图12 给出不同时刻模型的等效应力云图，各个时刻的应力分布差异明显。图13 给出结构层和防护层的破坏情况，图14 为圆筒套筒局部变形图。

图12 不同时刻模型的等效应力云图Fig.12 Contours of Effective Stress of Model at Different Time

续图12

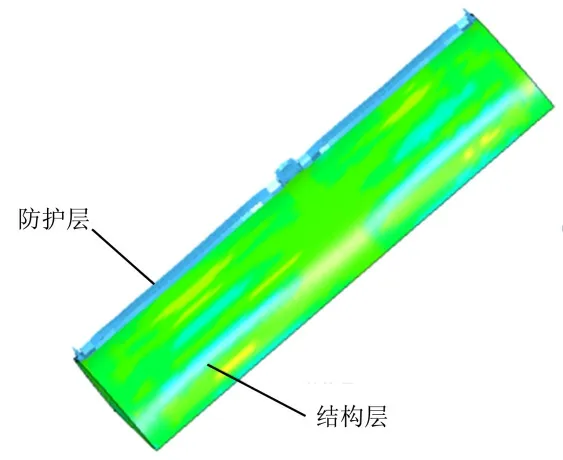
图13 结构层和防护层的破坏情况Fig.13 Damage of Structural and Protective Layers

图14 圆筒套筒局部变形Fig.14 The Local Deformation of The Coated Porous Cylinder

由图14 可知，结构层基本上是完好的、防护层发生了严重的破坏和层裂。圆筒套筒结构层变形量最大值不超过1%。防护层的破坏和分离吸收了大量的能量，减小了载荷对结构层的冲击，起到了保护套筒结构层的作用。

4 结 论

在多孔涂层材料的力学模型建模方面，本文针对一种涂层材料进行了冲击加载下材料的动态应力应变关系试验研究，对霍普金森压杆试验的结果进行的本构关系拟合，在材料损伤破坏模型的基础上，建立了涂层材料等效力学模型，确定了本构模型参数，并针对模型进行了数值模拟的比对，本构模型的数值模拟结果与试验结果有很好的一致性。由冲击加载下不同应变率时材料应力应变关系可以看出：冲击加载下材料的应力应变关系是正应变率敏感的；冲击加载下材料的应力应变关系没有线性弹性段，而表现出较强的非线性粘弹性特征。在此基础上采用有限元方法模拟计算了有涂层和无涂层材料的防护情况下筒状壳体在冲击载荷下的动力学响应。从而通过数值模拟方法考察了该多孔涂层材料对强冲击载荷的缓冲性能。这对于改进工程应用领域中一些需要进行结构缓冲设计的装置具有重要的工程价值。