一类带有绝对值的线性规划MATLAB 求解方法在数学建模教学中的应用

莫洁安

（广西民族师范学院数学与计算机科学学院，崇左532200）

0 引言

线性规划（Linear Programming，LP）是最简单、应用最广泛的一种数学规划方法，也是应用最早的一种优化方法，自从1947 年Dantzig 提出的单纯形法使得线性规划算法逐渐趋于成熟，在理论上发展到现在已经是比较成熟，同时在实际应用中更加的广泛与深入，特别是在计算机能大规模处理成千上万的约束条件和决策变量的线性规划问题之后，线性规划的适用领域就更为广泛了。线性规划的基本性质有：如果可行域是非空，则是一个凸集-凸多面体；如果有最优解，则最优解在可行域的顶点；如果可行域有界且只有有限个数的顶点，则最优解存在且在有限个数的顶点中；最优解由最优顶点的有效约束形成的方程组的解来确定。

对于线性规划的各种研究也很有很多深入的研究，常用的求解方法有单纯形法与内点法。一般的线性规划问题使用单纯形法可以通过变换转化成线性规划的标准形式进行求解，但是对于大规模的线性规划问题中，单纯形法显得有点吃力，这时，内点法的快速发展填补了单纯形法的获得最优解的收敛速度等问题，使得线性规划发展的更加快。利用线性规划求解问题的步骤一般为“确定决策变量、目标函数、约束条件、非负约束和求解”五个步骤，为了方便求解，通常需要将之化为标准形式。

在实际教学过程中，运用数学规划求解问题的时候的会遇到各种各样的问题，例如在《数学建模算法与应用》课程里有一个比较典型的案例---可以转化为线性规划的问题，其中规划问题为：

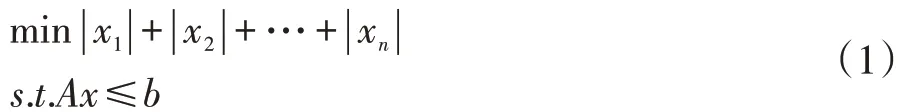
其中x=[x1,x2,…,xn]T，A和b为相应的矩阵和向量。

该目标函数的变量含有绝对值的问题，一般来说，求解的时候可以通过一些变换转化成线性规划，这时可令任意xi，存在ui,vi≥0，存在满足以下条件：

因此，记u=[u1,u2…,un]T，v=[v1,v2…,vn]T，上述的线性规划问题（1）式子可得：

转化成线性规划的标准型求解之后，这时可以运用MATLAB 中求线性规划问题的函数linprog（），该函数包含了求解线性规划问题的好几种算法，例如单纯形法和内点法。可以把上述式子改成线性规划求解的MATLAB 标准型即得：

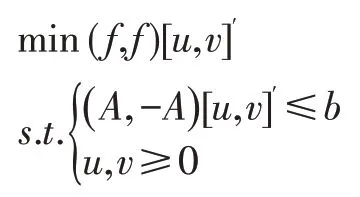
上式中，f表示目标函数的系数矩阵，A和b为线性不等式约束条件相应的矩阵和向量，运用MATLAB软件自带的linprog（）函数来求解该类线性规划问题，其中函数用法是：[x，fval]=linprog（c，A，b，Aeq，beq，lb，ub，options），这里的x 表示取得最优值的时候x 变量的取值，fval 表示最优值，c 表示目标函数的系数，A 和b表示线性不等式约束条件的系数矩阵，Aeq 和beq 表示线性等式约束条件的系数矩阵，lb 和ub 表示变量的取值范围，lb 表示最小值，ub 表示最大值，options 表示对该求解函数的高级应用，例如定义初始值、定义用具体哪个方法求解等等，这里一般用默认的方法求解即可。本案例的求解代码如下：

从该例子可以知道，目标函数中含有绝对值的情况可以转化成线性规划问题，相当于把变量的维度升高，对目标函数及约束条件的变量也是如此，在用MATLAB 求解处理的最终变量的结果要注意转化成x，因为算出来的是u，v的值，用x=u-v即可求得。

1 各类带绝对值的线性规划讨论及求解

对于课堂中教学的时候遇到上述问题（1）式中，按照正常的教学模式，该案例讲解完毕学生也能快速掌握该问题的处理方法、推导过程和MATLAB 求解的过程，接下来需要对该问题进行试探性的探讨与反思，例如启发学生进一步思考一下：目标函数的变量含有绝对值这种情况可以这样处理，那么如果是约束条件出现该怎么处理呢？或者是目标函数的变量没有含绝对值，约束条件有怎么办？或者是目标函数和约束条件均有绝对值的变量，这该如何处理呢？

因为在实际运用的过程，各种可能都会发生，特别是数学建模的课程，本身比较强调学生需要多角度思考、多方面考虑各种情况和条件的，因此接下来可以启发学生进行思考，通过对该问题的进一步提出假设问题，并根据已学习的案例进行推导、计算，达到一举多得的教学效果，接下来进行下面的探讨和求解：

（1）如果约束条件中含有绝对值变量呢，该如何处理？把该问题引出新的求解问题如下：

其中x=[x1,x2,…,xn]T，A和b为相应的矩阵和向量。

那么求解该问题的时候，可以根据上述问题（1）的求解过程接着进行，同理也可以转化为线性规划问题，因此，记u=[u1,u2…,un]T，v=[v1,v2…,vn]T，上述的线性规划问题（3）式可得：

把上述（4）式写成线性规划求解的MATLAB 标准型即得：

上式中，f表示目标函数的系数矩阵，A和b为线性不等式约束条件相应的矩阵和向量。因此，可以用MATLAB 的linprog（）函数来求解该类线性规划问题，代码如下：

从这里可以的简单推导和计算过程可以看出，虽然是基于问题（1）的扩展讨论，但是对问题的分析和求解过程是举一反三的一个很重要的案例，同时也激起学生对该问题的进一步探讨研究，提高学习的兴趣与参与程度，对课堂而已，这里对问题的拓展既包括难度合适以及引导学生动脑筋思考的双重考虑，也是对学生学习能力的一次检测。

（2）接下来，在（1）的基础上进一步讨论：如果添加等式约束条件呢？那么该问题为：

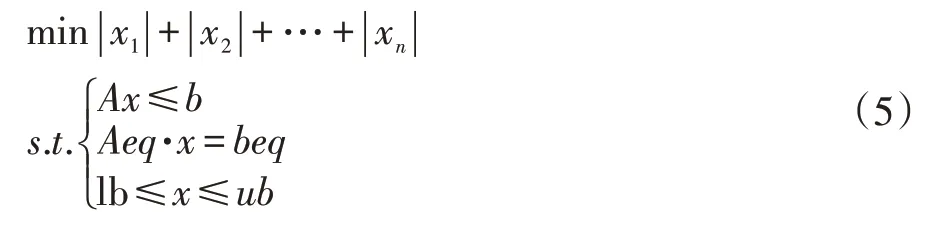
其中x=[x1,x2,…,xn]T，A和b为相应的矩阵和向量，lb 和ub表示变量的范围。

该问题比之上述问题稍稍有点麻烦，主要是添加了变量的取值范围，这时，对于含有绝对值情况讨论的时候有点不一样，哪里不一样呢？可以引导学生对上述问题重新进行推导，这时会发现，推导过程的时候，需要把变量的取值范围加进来考虑，因此，求解该目标函数的变量中含有绝对值的问题，参考上述（1）式中转化成线性规划的求解过程，记u=[u1,u2…,un]T，v=[v1,v2…,vn]T，上述的线性规划问题式子可得：

把上述（6）式写成线性规划求解的MATLAB 标准型即得：

上式中，f表示目标函数的系数矩阵，A和b为线性不等式约束条件相应的矩阵和向量，lb 和ub表示变量的范围，这里需要注意的是不等式矩阵里的1 表示的不是一个数字1，是一个1×n的向量矩阵。可以运用MATLAB 的linprog（）函数来求解该类线性规划问题，代码如下：

通过本例中的推导可以看出，这里的求解和推导过程比上述第一种情况难度稍微大一点，主要考虑到变量的取值范围对替换变量之后的转变，这时引导学生应该注意对该问题转化的认知，对含有绝对值的变量进行线性转换的过程的认识，从而达到更加深刻理解和认识该问题的推导与求解过程。

（3）根据以上1、2 讨论的情况的，可以进一步综合分析，引导学生思考：若目标函数及约束条件的变量中均含由绝对值的情况，这时该如何处理？有了前面两种情况的讨论，那么对于这个更加复杂的问题，可以有一定的基础和经验进行了。如对线性规划标准型带有绝对值的模型如下所示：

同理，把上面的问题转化成线性规划问题，记u=[u1,u2…,un]T，v=[v1,v2…,vn]T，该线性规划问题的MATLAB 标准型可以得：

上式中，f表示目标函数的系数矩阵，A和b为线性不等式约束条件相应的矩阵和向量，lb 和ub表示变量的范围，需要注意的是不等式矩阵里的1 表示的不是一个数字1，是一个1×n的向量矩阵，可以用MAT⁃LAB 的linprog（）函数来求解该类的线性规划问题，代码如下：

通过由浅入深一步一步的引导学生进行推导、计算到最好求解的过程，既符合数学建模课程举一反三的思想，也满足引导学生进行探讨式学习的需要，一举多得。

2 应用举例及结论

上述部分主要讲解理论推导及MATLAB 的计算函数，接下来举个具体的案例进行分析，求解下列线性规划问题：

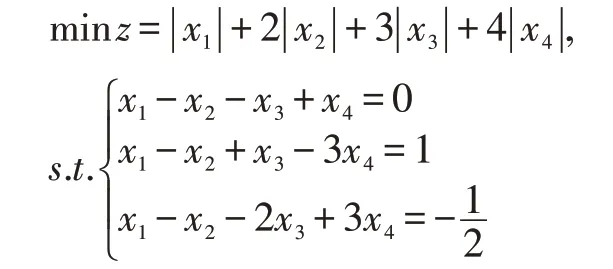
把上述问题转化成线性规划MATLAB 求解标准型，即：

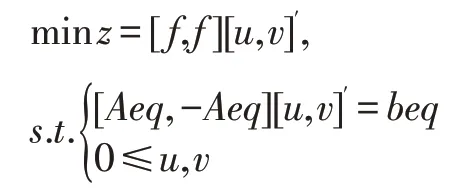
其中f、A、b矩阵如下所示：

根据本文上述的线性规划标准型的MATLAB 求解方式，其运行代码如下：

在实际过程中处理线性规划问题的时候，有些问题看起来不是线性规划问题，例如目标函数或者约束条件的变量带有绝对值情况，本文通过一些线性变换即可转化成标准的线性规划问题进行求解，并且讨论了其含有绝对值变量情况，由浅入深、一步一步引导学生进行思考、推导及其求解过程。

总而言之，在实际过程中处理线性规划问题的时候，有些问题看起来好像不是线性规划问题，这时可以通过一些线性变换转化成线性规划问题来处理。因此本文对该类问题进行深入探讨分析，综合得出一个针对各种情况中变量含有绝对值的求解情况并给出MATLAB 求解方法，给该课引入举一反三思想，达到理论学习与实践能力双向丰收的教学效果。