一种复杂背景下QR 码校正方法

孔庆鑫，潘卫清，戴恩文，沈艳婷

（1.浙江科技学院机械与能源工程学院，杭州310023；2.浙江科技学院理学院，杭州310023；3.中国科学院上海光学精密机械研究所，上海201800；4.浙江科技学院理学院，杭州310023）

0 引言

快速响应（QR）码信息存储量大，抗损性强，在各个领域中得到广泛应用。但其属于高密度条形码，在图像采集过程中，光学系统点扩展函数会使码图像的边缘出现重叠和模糊[1]。一般来说，二维码检测的研究大多是基于提高采集图像的质量或确定二维码的准确轮廓。例如，在文献[2]中Liu Y.使用基于移动端的图像处理系统，将二维码二值化、定位、分割和解码。文献[3]中，使用二维码设计了一种涉密信息的屏幕-摄像头传输系统，将需要加密的信息流按照二维码容量分割存储入若干张二维码中，利用摄像头采集二维码图像进行解码和解密信息，实现了网络隔离的情况下的数据传输。但其在图像定位算法上仍有欠缺，在复杂环境下的定位精度较低，无法满足大批量动态二维码流的快速定位解码。文献[5]提出了一种基于相关匹配的QR 码识别办法，使用曲面几何自适应分割图像，利用Hough 变换和控制点变换校正失真，最后用模板对QR 码进行相关匹配。但Hough 变换法要求图像周围无其他直线干扰，极易产生误差，且无法处理图像畸变问题[6]。文献[7]运用形态学算法解决了二维码附着在不规则表面引起的图像扭曲失真问题，但当QR 码的旋转角度过大时无法确定顶点的顺序。

本文为提高QR 码在复杂背景下定位及校正精度，使其能更好应用于屏幕-摄像头二维码通信中。根据QR 码自带结构特点，提出了一种在已知版本号下的快速识别方法。

1 图像预处理

对采集到的含有QR 码的图像预处理效果是能否正确检测二维码的关键，通常使用手机或电脑设备抓拍的图像存在阴影、反光、图像旋转或几何失真等问题。为了尽可能保存图像信息，减少背景和噪声的干扰，使用最大类间方差法对图像进行二值化处理。给出两类的类间方差公式：

为了得到图像分割的最佳阈值，必须使类间方差达到最大，即令t=arg maxσ2。二值化后图像效果如图1 所示。

图1 二值化

由于屏幕-摄像头通信CMOS 摄像头成像会产生动态条纹干扰，均值滤波会造成图像边缘模糊，不合适用于QR 码图像处理。中值滤波会删除原始图像中细线等细节，对QR 码图像的影响较小。中值滤波可以有效处理摄像头拍摄屏幕显示器引起的像素条纹问题。本文中使用3×3 邻域中值滤波。

2 QR码定位

在基于二维码的屏幕-摄像头通信通信系统中，将会处理大量的二维码数据流，对二维码四个顶点坐标的精确度要求较高，传统的二维码顶点坐标求取方法存在一定的缺陷。根据二维码的符号结构，本文首先设计了一个简单的算法找到二维码顶点坐标，使用回字位置探测图形高效准确地定位二维码位置。在定位二维码位置后，通过透视变换和重采样来恢复扭曲失真的图像，通过Reed-Solomom 误差修正算法得到纠错后的数据。实验表明，在该算法在复杂背景下有较好的效果。

2.1 定位符特征

由于QR 码符号的特殊性[1]，因此，我们可以检测出定位探针图形A、B、C 之间的距离关系，最终可以确定位置检测图形。如图2（a）所示，二维码符号的位置模式包括三个位置检测图形，分别位于左上角、右上角和左下角。从图2（b）可以看出，当一条水平线L 与垂直线H 通过检测图形中心时，从左到右均是基于深、浅，它们按1:1:3:1:1 的比例逐一出现，具有不同的旋转角度。而这一比例的图形特征检测不随二维码图像的大小和旋转而改变，因此可以利用这一特征来寻找回字定位图形的位置。

图2 QR码符号特征

2.2 定位算法

（1）扫描图像的每一行，并保存黑白模块的长度。

（2）记录每一个具有连续5 个像素颜色的行，计算并提取它的比例。

（3）检查比例是否符合1:1:3:1:1，且第一个像素模块为黑色。

（4）如果c 正确，则找到回字定位中心位置，即中间的黑色块，保存该列连续的黑白模块长度，最后对列重复步骤b、c。

（5）在列查找过程中再次检查回字中心位置，如果该中心点符合行查找模式中误差范围，保存新的中心点位置，反之，检查下一行。对所有符合比例的行、列值进行求和取平均，即理论上回字中心位置，由于图像可能出现模糊、变形等因素，出于容错考虑，上下各8个像素值所有符合搜索比例的点进行存储。

2.3 使用K-means对候选点集群聚类

运用K-means 聚类算法对回字定位点候选集群进行聚类，选取与整体差异最小点作为初始聚类中心，据此实现特征点匹配可大大降低计算维度。对存储的候选点通过无监督学习的方式，进行K-means 聚类，得到3 个搜获集群，从中选择出三个点，即三个回字中心位置。以下为K-means 算法步骤：

（1）为待聚类的点S=x1,x2,x3…xn寻找聚类中心u1,u2,u3…uk。

（2）利用误差平方和准则函数作为聚类准则，计算每个点到聚类中心的距离，将每个点聚类到离该点最近的聚类中去。

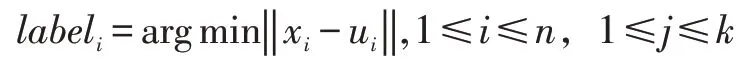
（3）计算每个聚类Cj中所有点的坐标均值uj

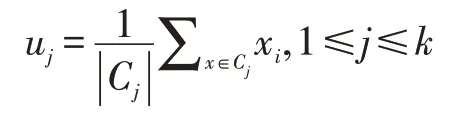
（4）将这个平均值uj作为新的聚类中心反复执行（2）、（3），直到聚类中心不再进行大范围移动或者聚类次数达到要求为止。

通过上述聚类算法，相似程度较高的项目被分配到同一类中。聚类算法的执行过程较为耗时，但可以离线进行，因此并不影响算法实时性。

2.4 判断回字定位点顺序

使用三点之间向量点积算法判断出三个回字定位点的顺序。下面用伪代码表示：

此处可知三个点顺序如图3 所示。

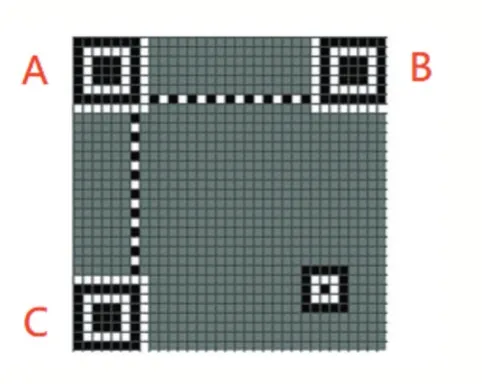
图3 QR码回字探测图形顺序图

2.5 寻找校正图形

在找到二维码的三个回字定位图形后，需要检测二维码的校正图形，完成二维码的精确定位。相比回字定位标志，校正图形更加难以定位，单一水平与垂直检测会产生极大误差。本文对传统校正图形定位方法做了改进。将校正图形最外部黑色正方形作为分隔符，改为水平、竖直搜索内部符合1:1:1 比例的图形。在已知三个定位图形坐标及顺序的情况下，估计出校正图形中心理论位置，在对角搜索算法下，取与理论距离最近的候选点作为实际校正图形中心坐标。

在找不到校正图形，或版本1 的QR 码不存在校正图形的情况下，本文根据二维码的设计特点，设计了理论求解二维码4 个顶点位置的算法。

（1）计 算A 点 到B，C 两 点 的 归 一 化 向 量二维码中心坐标

（2）计算得三个回字定位坐标各自距离，记dist_AC，dist_AB。得各自方向上每个格子所占像素个数为cell_width=dist/（module-7）。

（3）求取扭曲图像中定位图形之间的最大距离，dist_max=max（dist_AC，dist_AB）。

（4）回字定位符A 的四个顶点坐标求法如下所示。

B，C 两点同样用以上办法求出。位置顺序如图4所示。

（5）由于版本1 的QR 码不存在校正图形，且需要在无法找到校正图形的情况下精确定位右下角坐标，不能直接用校正图形推出最后一点坐标时，以下给出该坐标求取方法。

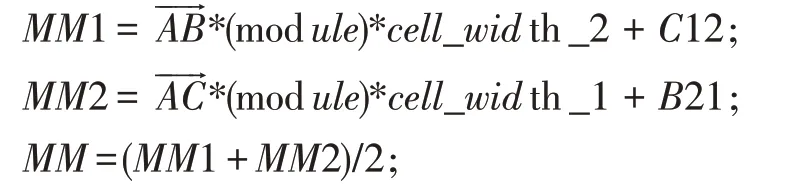
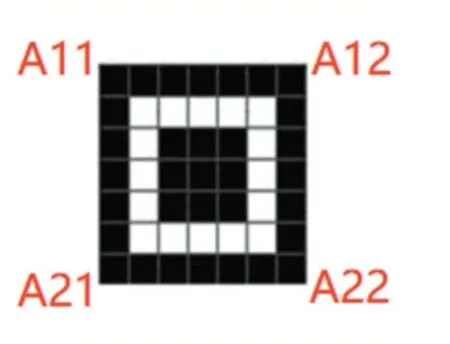
图4 探测图形顶点顺序图

3 QR码校正

在三个回字定位坐标及校正图形均正确找到的情况下，可以根据二维码设计标准推测出图像的四个顶点，然后通过逆投影变换将扭曲失真图像进行校正，如图5 所示。

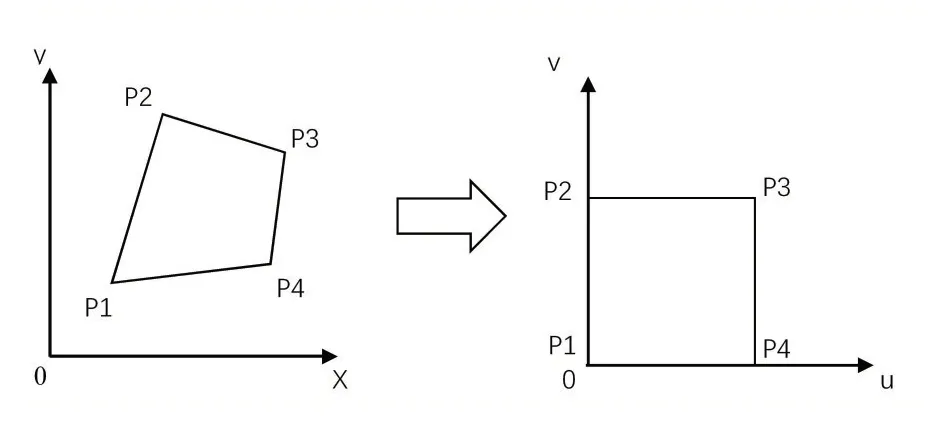
图5 逆投影变换

设（x，y）为原始图像上二维码坐标，（u，v）为投影变换后的校正坐标，a，b，c，d，e，f，g，h 为公式中待解的8 个参数，将至少4 点代入公式中求解上述参数，这里在已知二维码版本号的前提下，可以选取三个回字定位中心坐标和校正图形中心坐标进行校正。

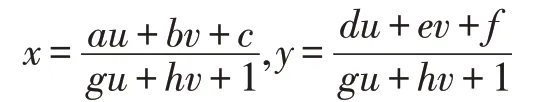
整理后得到：

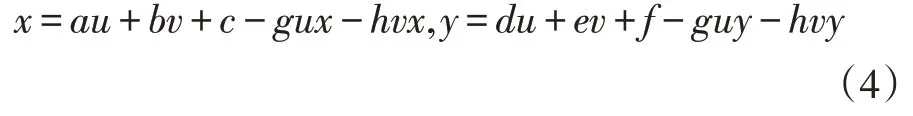
将 二维 码 扭曲 失真 坐 标(x0,y0)、(x1,,y1)，(x2,y2)，(x3,,y3)和校正顶点(u0,v0)、(u1,,v1)，(u2,v2)，(u3,,v3)代入投影公式中，再将原始QR 二维码图形转换到一个正方形内，设正方形边长为W，转换后4 个顶点坐标可以分别取(0,0)、(w,0)，(w,w)，(0,w) ，将以上4 点坐标代入（4）式中解得：

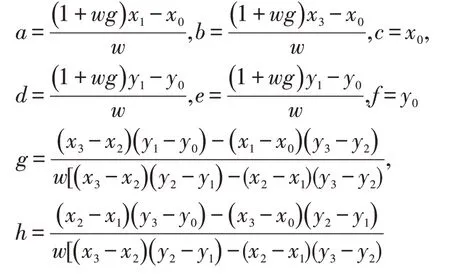
校正结果如图6 所示。

图6 QR码校正示意图

4 实验结果与分析

4.1 复杂背景下的定位结果

为了验证本文算法性能，利用Intel Core i5-7500CPU @3.2GHz 计算机，使用MATLAB 2017a 软件上实现本文算法，并测试运行速度及复杂背景下的识别情况。

本文算法以文献[13]中形态学和Hough 变换算法对图像的处理结果说明精度对图像处理的影响。该算法通过形态学图像处理与边缘检测得到QR 码边缘图像，然后通过Hough 变换找到QR 码顶点。如图7（b）所示，但经过图像放大，QR 码边缘存在间隙，如果直接建立采样网络解码，会造成部分采样点信息错误，由于QR 自身的纠错机制，在不超过纠错等级的前提下并不影响信息解读，但是单张QR 码容量有限，使用更低的纠错等级就可以存储相对更多的信息。如果定位精度低，会降低对QR 码最大容纳信息量。

图7 文献[13]中定位算法

使用本文算法定位二维码效果如图8。

图8 本文定位算法效果图

4.2 算法识别正确率

一般情况下，摄像头分辨率越高，图片细节信息更加丰富，有利于条码识别，但信息量越大，处理速度会更慢。本次实验使用目前手机通用960×544 像素普通摄像头对QR 码进行采集。拍摄角度分别为上、下、左、右四个方向上与桌面呈现30°-90°各200 幅，镜头距离10-20cm 变化，模拟QR 码的几何失真，共采集800 幅图。

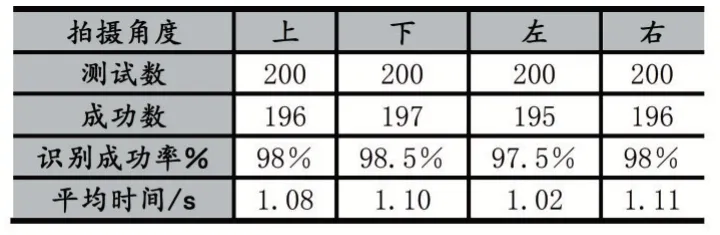
表1 实验数据统计结果

比较传统算法和本文提出的QR 码定位识别算法，在识别时间上与国标算法略快，但在识别率上有较大幅度提升。当找不到校正图形时，通过算法可以有效推测出坐标位置。相较于文献[8]中扫描办法，从图像右下角向内扫描时，QR 码边界像素在底部聚集较密集，导致边缘两条直线相交于QR 码内，而非边缘顶点，因此算法无法找到对应顶点。本文在扫描时进行K-means 聚类剔除冗余点，能够有效较低冗余点对定位精度的影响，从而可以将扭曲失真二维码进行亚像素级校正。整个算法在相对较短的时间内达到了较高的识别率，在嵌入式设备、手机移动端均可以满足实时性要求。

4.3 不同算法性能比较

本文使用文献[11]中的实验条件，分别测试QR 码在旋转与角度失真情况下的定位正确率。如图9（a）中，旋转角度0°～150°，步长30°，图9（b）透视畸变0°～35°，步长5°。

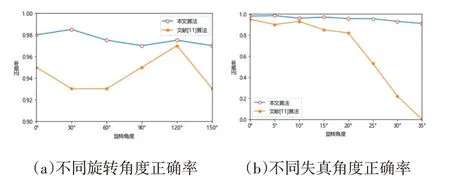
图9 旋转与失真角度下误差对比

从实验结果来看，本文算法可以忽略旋转带来的影响，35°以内的透视畸变均可保持90%以上正确率，为后续解码提供保障。对比文献[11]中使用轮廓追踪，当透视角度过大后，不同角度的回字定位点轮廓的最小水平包围矩形长宽比会发生变化，其参数为实验调整数据，无法满足数量较大且情况不同的二维码数据流采集校正要求，在实验条件下其透视畸变角度大于10°后校正正确率处于90%以下，已不具备解码条件。

同样在文献[12]的实验条件下，比较QR 码定位算法的正确率及运行速度。实验结果如图10 所示，相比于文献[12]中使用七个方向对定位点进行扫描，使用欧氏距离计算距离误差来剔除冗余点，本文算法只采用两个方向扫描定位点，然后使用K-means 聚类剔除冗余点，可以离线进行，计算量更低，且定位更加精准，更适合与屏幕-摄像头通信中对大量二维码数据流的处理。如图8 所示，本文算法具有更快的运行时间和更高的QR 码校正成功率。

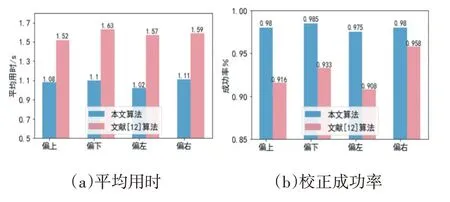
图10 本算法与文献[12]算法对比

5 结语

针对使用动态二维码的屏幕摄像头通信方式，本文设计了一种抗复杂环境的QR 快速定位校正办法，能够有效地对QR 码进行定位和校正，提高了识别速度，在校正算法上实现了亚像素级别的图像校正，使得发送端传输的QR 码可以在低容错版本的情况下保持相对较高的有效信息存储，下一步工作是进一步简化算法，开发基于二维码的屏幕摄像头的通信系统，实现信息的高速传输。