某土工膜堆石坝帷幕后水位偏高成因初步分析

姜宇航 戴妙林 刘晓青

摘 要：某土工膜堆石坝的坝基防渗体系包括趾板及坝基帷幕，帷幕后实测水位偏高，与上游水位连通性较强，需要对其成因进行分析。基于渗流观测资料建立回归模型进行初步分析，运用正交试验设计和渗流有限元计算生成训练样本，对各影响因素进行敏感性分析。借助支持向量机在小样本中的高度非线性映射能力，建立渗流参数与渗压水位的对应关系。采用遗传算法对支持向量机模型进行参数优化，以支持向量机预测值与实测值误差作为适应度值，对坝基地层和防渗体各区域渗流参数进行优化搜索，并将反演结果进行反馈计算验证。结果表明，基于支持向量机-遗传算法反演渗流参数是可行的，帷幕后渗压水位偏高由趾板与帷幕间的裂缝及坝基渗流各向异性综合引起，可针对上述薄弱部位进行工程处理以降低幕后水位。

关键词：土工膜堆石坝;回归模型;正交试验设计;敏感性分析;支持向量机;遗传算法;渗流参数反演

中图分类号：TV698.1   文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.07.021

Abstract：The anti-seepage system of a geomembrane rockfill dam includes a toe board and a dam foundation curtain. The measured water level behind the curtain is higher and it has stronger connectivity with the upstream water level， and its cause needs to be analyzed. A regression model was established for preliminary analysis based on the seepage observation data. It used orthogonal experimental design and seepage finite element calculation to generate training samples and conduct sensitivity analysis of each influencing factor. With the support of the highly non-linear mapping capability of support vector machines in small samples， the correspondence relationship of seepage parameters and seepage pressure levels were established. The genetic algorithm was used to optimize the parameters of the support vector machine model and the error between the predicted value and the measured value of the support vector machine was used as the fitness value. The seepage parameters of the dam base layer and the impervious body were optimized and searched. The results were verified by feedback calculations. The results show that inversion of seepage parameters based on support vector machine-genetic algorithm is feasible， and the high level of seepage pressure behind the curtain is caused by the cracks between the toe plate and the curtain and the anisotropy of dam foundation seepage. The above weak parts are engineered to lower the water level behind the scenes.

Key words： geomembrane rockfill dam; regression model; orthogonal test design; sensitivity analysis; support vector machine; genetic algorithm; inversion of seepage parameters

在大坝蓄水和运行过程中，受各种因素的共同作用，部分区域渗透系数偏大、渗压水位偏高。为了对其成因进行分析，需要结合坝基地质条件和防渗体可能存在的缺陷进行研究[1]。张兵等[2]运用正交试验设计，对云驾岭矿区岩层力学参数进行了敏感性分析与反演;Harrouni等[3]提出了運用优化理论识别含水层参数的方法;邓祥辉[4]采用遗传算法（GA）和有限元法进行了高坝工程渗流反问题研究;魏进兵等[5]运用遗传算法优化BP神经网络反演得到了滑坡体饱和渗透系数;万文新等[6]对坝基防渗墙可能出现的裂缝进行了渗流计算与研究。

土工膜堆石坝的趾板与坝基帷幕的接触部位相对薄弱，可能存在接触面裂缝，此外坝基岩体存在的渗流各向异性特性，呈现出与各向同性不同的特点。针对上述因素，笔者基于某土工膜堆石坝实测资料和数值计算等方法，进行影响规律和渗流参数的反演研究。近年兴起的支持向量机（Support Vector Machine，SVM）是基于数理统计理论建立起来的新型学习机器，具有适应性强、所需样本容量小和运行速度快等特点，且具有极强的非线性映射能力。通过对坝基渗流回归模型进行初步分析，基于正交设计方案与渗流有限元计算得到的样本，并借助支持向量机建立渗压水位与坝基渗流参数之间的预测模型，可以为反演渗流参数提供快速有效的途径。

1 工程概况

某土工膜堆石坝由复合土工膜、挤压边墙、垫层、过渡层、主堆石区、次堆石区和排水体等组成。挤压式边墙混凝土共202层，断面为梯形，边墙外侧坡比1∶1.6，内侧坡比8∶1，顶宽10 cm，底宽79 cm，墙高40 cm。上游沿坝面挤压边墙每隔6 m设置锚固带，锚固带由挤压边墙固定，土工膜与锚固带相连接。坝基设置防渗帷幕，土工膜与坝基面、帷幕之间采用混凝土趾板连接。坝顶高程515 m，趾板建基面最低高程430 m，最大坝高85 m，坝顶全长362.09 m，坝顶宽度为8.00 m。坝顶以上设4.2 m高防浪墙，上游坝坡1∶1.6，下游坝坡1∶1.8。

大坝最大剖面渗压计DB-A-P-01～10观测布置见图1，其中位于土工膜后的渗压计DB-A-P-08 10渗压实测值为0，说明坝体浸润面低于仪器所在高程，DB-A-P-06仪器损坏无数据。

2 实测渗压水位分析

帷幕后从高到低依次布置渗压计DB-A-P-03、DB-A-P-02、DB-A-P-01，用于监测帷幕后渗压水位。帷幕下游沿坝基面依次布置渗压计DB-A-P-04、DB-A-P-05、DB-A-P-07，用于监测坝基面渗压水位，实测渗壓水位如图2所示，帷幕后3个测点2016年和2017年最高水位、最低水位和年变幅见表1。从实测渗压水位来看，DB-A-P-01～03渗压水位与上游水位相关性较为密切，而DB-A-P-04～05和DB-A-P-07受上游水位变化程度影响不明显。DB-A-P-01～03测值和下游水位的差值与上下游水位差值之比分别为0.72、0.69、0.86，数值偏大，表明这3个测点水位偏高。

由表2可知，DB-A-P-01 03的上游水位分量较大，且受上游水位变化影响程度从高到低为DB-A-P-03、DB-A-P-01、DB-A-P-02，与测点水位高低顺序是一致的。以上分析表明，DB-A-P-03测点与上游库水连通性相对较强。

4 数值计算分析

4.1 计算模型和参数

Geo-studio为加拿大GEO-SLOPE公司开发的二维有限元软件，其中SEEP/W模块可用来分析多孔隙介质渗流状态与孔隙水压力消散过程。本文涉及土工膜、防渗帷幕的模拟，由于该软件可模拟各向异性渗流，且计算结果较为合理准确，因此采用其进行计算和研究。假设坝体渗流为层流并满足达西定律，建立有限元计算模型，模型范围坝基面上下游侧各取200 m，深度取180 m，并包含坝基防渗帷幕，地基两侧及底部施加边界约束。根据设计资料对不同区域赋予渗透系数，各材料设计渗透系数见表3。采用2017年1月6日水位工况即上游水位508.25 m、下游水位440.32 m进行计算。鉴于坝体上游铺设的土工膜厚度仅为3.5 mm，若以此作为边长来剖分网格单元，不仅计算精度无法保证，而且会因单元畸形而造成计算溢出。为此，在实际有限元计算中依据渗流量等效原理，适当增大复合土工膜的计算厚度与渗透系数，使计算精度不受影响[7]。

4.2 基于正交试验设计的渗流参数敏感性分析

4.2.1 坝基地层与防渗体参数选取

趾板与土工膜和坝基防渗帷幕连接，其自身的渗透系数较小，考虑到趾板与帷幕连接部位有可能存在缺陷，故在趾板与帷幕连接处设置宽度为10 cm的等效裂缝，该值为设计软件所允许的最小宽度，并与上游库水连通。裂缝渗透系数采用裂隙渗流立方定律进行估算，为6.29×10-3 m/s，故裂缝渗透系数范围取1×10-3～1×10-2 m/s。考虑到坝基地层为砂质板岩，可能存在各向异性的渗流特性[8]，故将坝基垂直层向渗透系数Kn、顺层向渗透系数Ks与垂直层向渗透系数Kn的比值Ks/Kn以及Kn与水平向夹角θ作为影响因素。防渗帷幕深度为30 m，渗透系数取值范围为1×10-7～9×10-7 m/s。

4.2.2 基于正交试验方案的敏感性分析

正交试验设计是依据正交性原则，从所有试验中挑选出最具有代表性的试验组进行试验，这些代表性的试验组具有均匀分散、齐整可比的特点，极大地简化了多因素多水平情况下的设计试验组数，是一种高效、快速、经济的试验方法[9]。将Kn、Ks/Kn、θ、帷幕的渗透系数K帷幕以及裂缝渗透系数K裂缝作为影响因素，由此设计出25组试验的5因素5水平正交表，坝基渗透系数分组参数水平设置见表4。运用有限元软件对每一组试验进行计算，得到25组数据的正交试验表。

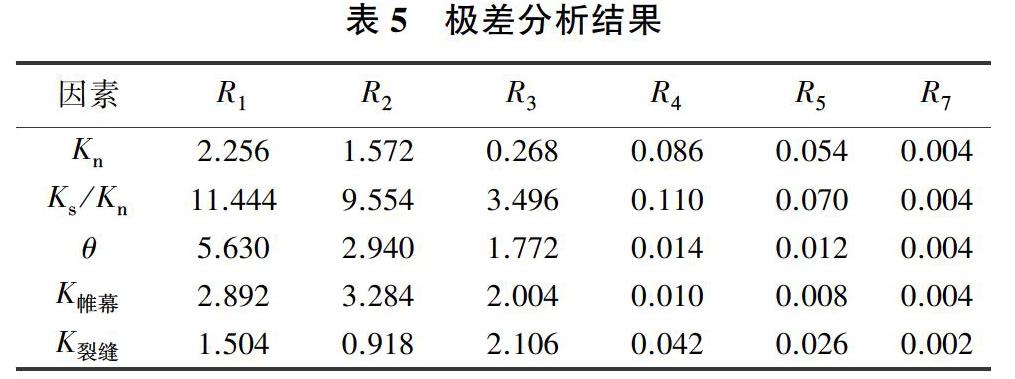
通过计算极差Rj进行极差分析可以对正交试验各因素的敏感性进行评价[10]，极差Rj越大，说明因素水平改变对结果的影响越大，即敏感性越大;极差Rj越小，说明因素水平改变对结果的影响性越小。正交试验数据极差分析结果见表5，其中R1～R7分别为DB-A-P-01～07测点各因素极差。结果显示，因素水平改变对DB-A-P-01～03测值影响程度较大，对DB-A-P-04～05和DB-A-P-07测值影响较小;对DB-A-P-01测值影响程度较大的因素为Ks/Kn、θ、K帷幕;对DB-A-P-02测值影响程度较大的因素为Ks/Kn、K帷幕、θ;对DB-A-P-03测值影响程度较大的因素为Ks/Kn、K裂缝、K帷幕。

5 渗流参数反演

5.1 构建支持向量机预测样本

因为有限元软件GEO-slope不支持其他程序调用，所以在参数反演优化计算过程中无法直接调用此软件计算测点水位。为解决这个问题，在反演渗流参数之前，首先建立因变量y（各监测点水位）与自变量x（待反演渗流参数）之间关系的预测模型。借助预测模型，可以计算得到待反演渗流参数任意取值组合的各测点水位预测值，用于反演分析中预测值与实测值误差的计算。当因变量y与自变量x之间无确定性解析表达式时，建立预测模型的方法有神经网络和支持向量机等智能学习方法。支持向量机由Vapnik首先提出，可用于模式分类和非线性回归，它的理论基础是统计学习理论，具有解决问题的有效性高、计算方法简单、运行速度快及理论完善等优点。在非线性回归中核函数K的选择至关重要，其种类主要有线性核函数、多项式核函数、径向基核函数（RBF）和sigmoid核函数。径向基核函数作为局部性核函数，只对测试点附近领域的数据点有影响，故适合作为通用模式的核函数[11]，本文选择径向基核函数进行非线性回归分析。