基于误差修正模型的黄河源区年径流预测
2020-10-12张金萍李红宾肖宏林
张金萍 李红宾 肖宏林

摘 要:为了提升黄河源区年径流预测精度以及了解黄河源区降雨、径流、泥沙之间的相互影响关系,以黄河源区唐乃亥水文站实测年降雨量、年径流量和年输沙量作为研究数据,采用协整理论分析方法,分别建立降雨—径流、径流—泥沙两变量误差修正模型以及降雨—径流—泥沙三变量误差修正模型,对研究区年径流量进行预测。结果表明:三变量误差修正模型的拟合优度均大于两变量误差修正模型的,模型解释性更强,更能定量表现黄河源区径流量—降雨量—输沙量之间的关系;三变量误差修正模型的平均相对误差为-4.83%,可以用于黄河源区年径流预测。
关键词:协整理论;误差修正模型;径流预测;黄河源区
中图分类号:P333;TV882.1 文献标志码:A
doi:10.3969/j.issn.1000-1379.2020.07.002
Abstract:In order to improve the accuracy of annual runoff prediction in the source area of the Yellow River and understand the relationship between rainfall, runoff and sediment in the source area of the Yellow River, the measured annual rainfall, annual runoff and annual sediment transport at Tangnaihai Hydrological Station in the source area of the Yellow River were taken as the research data. By using cointegration theory analysis method to establish rainfall runoff, runoff and sediment of two-variable error correction model and rainfall runoff-sediment three-variable error correction model, it predicted the annual runoff of the study area. The results show that the three-variable error correction model fitting is better than the two-variable error correction model and more explanatory, more quantitative performance relationship between the source region of the Yellow River rainfall-runoff sediment; the average relative error of the three-variable error correction model is -4.83%, which can be used to forecast annual runoff in the source area of the Yellow River.
Key words: cointegration theory; error correction model; runoff prediction; Yellow River source area
徑流量是河流的重要水文变量之一,准确预测河流径流量能够在一定程度上对防洪抗旱、灌溉发电起指导作用,对水资源的合理开发利用有着十分重要的意义。但是,受气象、人为等诸多不确定因素的影响,径流量具有较强的随机性,且随着预见期的延长,影响径流预测精度的因素也会增加,从而导致预报精度较低。实践中常见的用于预测河川径流的预测模型有自回归模型、人工神经网络模型和季节性自回归模型等[1-2],其中自回归模型局限于单因子分析以及年径流序列前后相依性较弱,使得模型的预测精度不高,难以达到理想的预测效果。误差修正模型(Error Correction Model,简称ECM)能反映变量的短期波动和长期均衡特征,是基于协整理论的一种常用模型,但目前在水文预报领域应用较少。张金萍等[3]运用协整理论建立误差修正模型,对渭河年径流进行了预测,证明了误差修正模型对河川年径流预测的适用性;畅明琦等[4]将协整理论引入河川径流分析中,利用黄河兰州站和花园口站年径流序列建立误差修正模型并对下游径流进行预测;张利亚等[5]利用误差修正模型对松花江流域下游年径流量进行了预测,结果表明模型预测是有效的。
本文以黄河源区为研究区域,根据唐乃亥水文站的降雨、径流、泥沙观测资料,运用协整理论分别建立降雨—径流、径流—泥沙两变量误差修正模型和降雨—径流—泥沙三变量误差修正模型[6],对黄河源区年径流量进行预测,以期为河川年径流预测模型的研究提供技术参考。
1 数据来源与模型构建
黄河源区位于青藏高原东北部,指的是黄河干流唐乃亥水文站以上的区域,该区域属于高寒半湿润气候区,面积为12.20万km2。黄河源区以占黄河流域15%的汇水面积贡献了黄河年径流量的33%,是黄河流域最重要的产流区,被称为黄河“水塔”,该区域径流量的变化对于整个黄河流域水资源的变化具有至关重要的影响和控制性作用[7]。本文以唐乃亥水文站1966—2013年48 a的径流量(W)、降雨量(P)和输沙量(S)作为研究数据,各变量的变化情况见图1。
由图1可知,唐乃亥水文站的年降雨量、年径流量和年输沙量变化趋势大致相同。选择1966—2005年40 a的数据进行建模,2006—2013年8 a的数据进行检验。本次研究分别建立3个误差修正模型进行对比分析:模型1,径流量—降雨量(W—P)误差修正模型;模型2,径流量—输沙量(W—S)误差修正模型;模型3,径流量—降雨量—输沙量(W—P—S)误差修正模型。
2 协整与误差修正模型
2.1 协整概念
协整描述的是时间序列之间所具有的长期均衡关系,若一个时间序列非平稳,经过一次差分后变为平稳序列,则称该时间序列为一阶单整,记为I(1);若经过d次差分后变为平稳序列,则为d阶单整,记为I(d);若时间序列本身为平稳序列,则记为I(0)。设两个时间序列Xt、Yt同为I(d),即Xt~ I(d),Yt~ I(d),若存在β,使得Yt-βXt成为I(0)过程,则称Xt和Yt具有协整关系。
2.2 平稳性检验
模型1(式(6))表明径流量受降雨量的影响,还受到上一年径流量偏离均衡水平的影响;ΔP的系数为0.653 320,说明降雨量对径流量的影响显著[10];误差修正项系数为-0.776 364,符合反向修正机制,说明本年径流量偏离均衡水平的差值在下一年将有77.6%得到调整。
模型2(式(7))表明径流量受输沙量的影响[11],还受到上一年径流量偏离均衡水平的影响,ΔS的系数为0.051 093,说明泥沙量对径流量的影响不显著;误差修正项系数为-0.647 311,符合反向修正机制,说明本年径流量偏离均衡水平的差值在下一年将有64.7%得到调整。
模型3(式(8))表明径流量不仅受降雨量和输沙量的影响,而且还受到上一年径流量偏离均衡水平的影响,ΔP和ΔS的系数分别为0.278 250、0.035 729,说明黄河源区降雨量与泥沙量对径流量的短期影响程度不同,降雨量要比泥沙量的影响程度强;误差修正项系数为-0.772 702,符合反向修正机制,说明本年的径流量偏离均衡水平的差值在下一年将有77.3%得到调整。
对比3个模型,误差修正项系数均小于零,表明误差修正项对W的变动具有反方向调节作用;3个模型的拟合优度R2值均大于0.8,拟合度都很好,模型3的拟合优度最大(0.924 724),较模型1、模型2的解释性更强;D.W.值均在2附近,说明残差序列没有自相关性;模型3较模型1、模型2的D.W.值小的原因是模型3从计量方程的统计学意义上讲增加了一个解释变量,会增大出现多重共线的可能性,出现自相关性的可能性增大。
3 模型模拟和预测
3.1 模拟分析
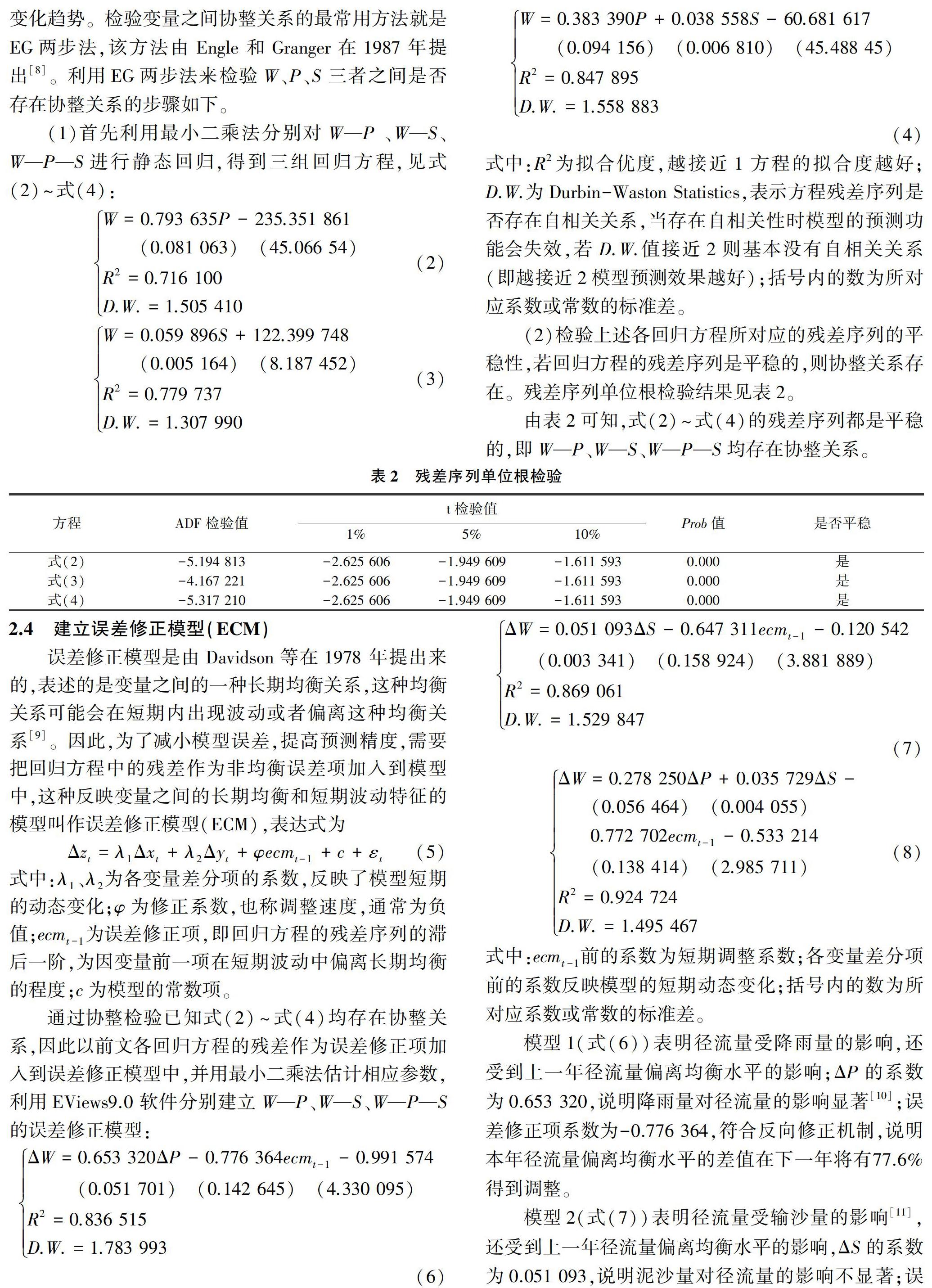
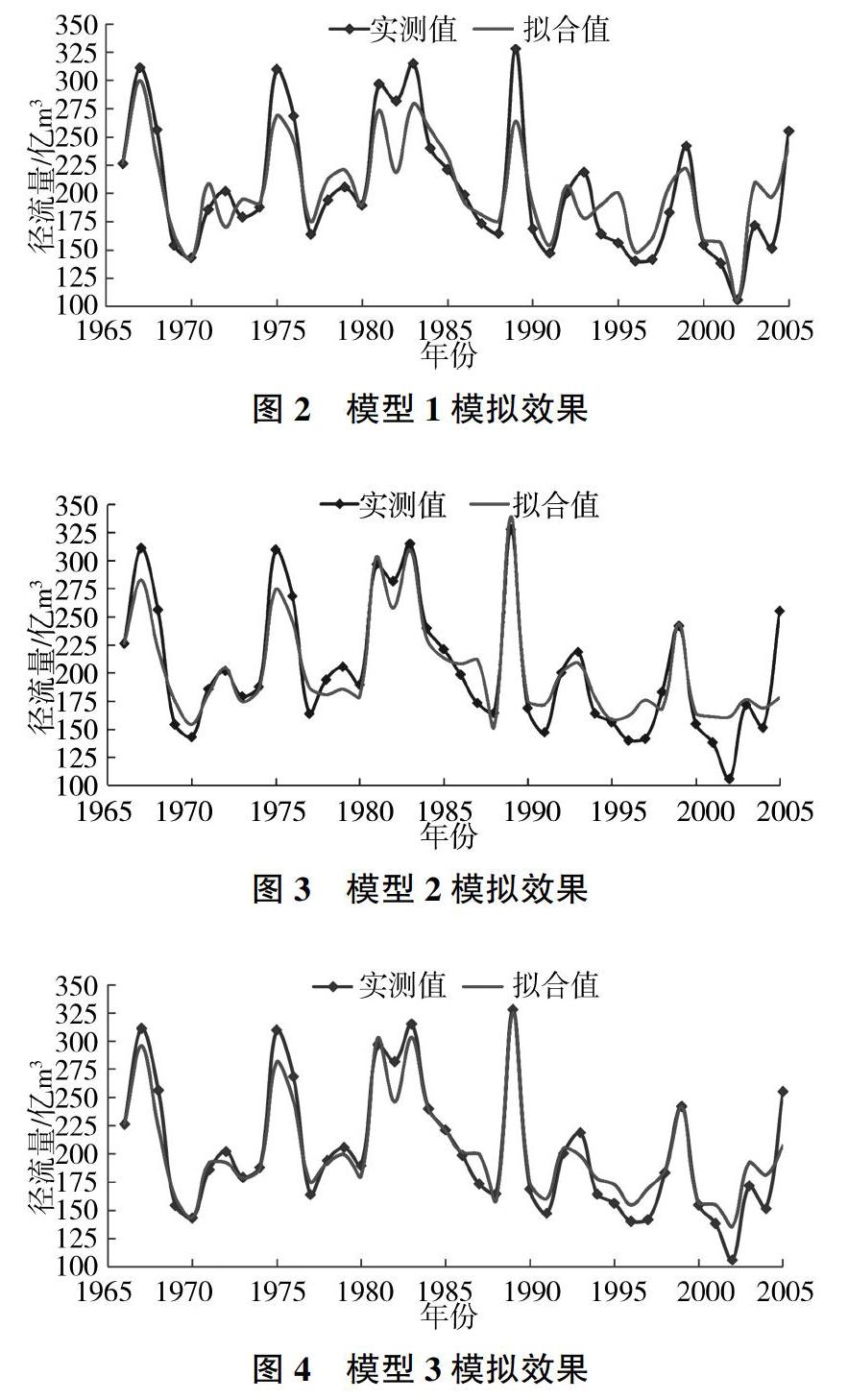
利用3个模型分别对黄河源区1966—2005年的年径流量进行模拟,结果见图2~图4。
由图2~图4可以看出, 3个模型的径流量拟合良好。通过计算,模型1~模型3在模拟期的平均相对误差分别为9.96%、9.49%、6.93%,由此可知模型3的模拟效果最好。
3.2 预测分析
运用3个模型分别对黄河源区2006—2013年的年径流量进行预测,结果见表3。
由表3可知,运用模型1、模型2和模型3预测黄河源区年径流量的效果整体良好,除個别年份外,预测相对误差基本能控制在20%以内。具体来看,模型1预测期内只有2006年的误差较大(28.08%)其余年份误差均小于20%,平均相对误差为7.12%;模型2测期内2006年、2009年、2012年的相对误差较大(分别为20.58%、-31.90%、-22.61%),其余年份误差均小于20%,平均相对误差为-12.47%;模型3预测期内只有2009年的误差较大(-22.37%),其余年份误差均小于20%,平均相对误差为-4.83%。由此可知,模型3的预测精度最高,预测效果最好。
4 结 论
(1)以黄河源区唐乃亥水文站降雨、径流、泥沙资料为依据,建立黄河源区年径流量预测误差修正模型,验证了协整理论和误差修正模型在水文预报方面具有很好的适用性,为河川年径流预报模型提供了新的方法和思路。
(2)通过对比分析,降雨量—径流量、径流量—输沙量、径流量—降雨量—输沙量误差修正模型均可用于年径流预测,但径流量—降雨量—输沙量三变量误差修正模型预测效果最好,可以用来预测黄河源区年径流量。
参考文献:
[1] 关静,梁川,王欣,等.雅鲁藏布江中下游径流预测方法的对比分析[J].黑龙江大学工程学报,2017,8(2):7-13.
[2] 梁川,潘妮.长江源高寒区域河川径流预测方法及其对比分析[J].南水北调与水利科技,2012,10(1):35-39.
[3] 张金萍,原文林,郭兵托.基于协整分析的河川径流预测[J].水电能源科学,2013,31(5):18-20,99.
[4] 畅明琦,刘俊萍.河川径流序列协整预测研究[J].应用科学学报,2005,23(6):109-112.
[5] 张利亚,张利平,曹枫林,等.基于协整与误差修正机制的径流预测模型研究[J].武汉大学学报(工学版),2006,39(6):6-9.
[6] 张祖欣.基于多变量误差修正模型与改进灰色理论的我国能源需求预测研究[J].华东电力,2012,40(10):1685-1689.
[7] 丁志宏,张金萍,赵焱.基于CEEMDAN的黄河源区年径流量多时间尺度变化特征研究[J].海河水利,2016,35(6):1-6.
[8] 郭兵托,孙素艳,张金萍,等.陆浑灌区供需水的协整关系研究[J].节水灌溉,2018,43(10):68-73,77.
[9] 高铁梅.计量经济分析方法与建模EViews应用及实例 [M].2版.北京:清华大学出版社,2009:177-180.
[10] 赵仁荣,陈海潮,朱松立,等.黄河源区径流变化及原因分析[J].人民黄河,2007,29(4):15-16,80.
[11] 彭红,郑艳爽,张明武.黄河源区汛期水沙变化分析[J].中国水土保持,2014,35(12):33-36,69.
【责任编辑 翟戌亮】
