河流-承压含水层系统压力传导系数的谱分析

吕国栋 杨启红 王俊智

摘 要：含水层对河水的响应程度与含水层的压力传导系数密切相关。借鉴多孔介质热运移的相关研究成果，推导得到了河流-承压含水层系统压力传导系数的功率谱解析表达式，进而提出了一种联合使用河水位和地下水位观测数据估算承压含水层压力传导系数的新方法。采用该方法，应用螺山水文站水位数据和洪湖地区承压地下水位数据，估算了长江洪湖地区承压含水层的压力传导系数，结果表明：该方法估算得到的压力传导系数为1.6×104～8.7×105 m2/d，平均值为1.8×105 m2/d，与非稳定抽水试验和数值模型反演得到的结果2.5×104～3.8×105 m2/d具有较好的一致性，功率谱分析是估算承压含水层压力传导系数的有效方法。

关键词：谱分析;河流-承压含水层系统;压力传导系数;地下水位;洪湖

中图分类号：X522   文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.04.016

Abstract： The response of aquifer to river is closely related to the aquifer diffusivity. By referring to studies of heat transport in porous media， this paper presented a power spectral method to estimate the confined aquifer diffusivity. This method was applied to the Honghu Lake area of the Yangtze River. Fluctuations of the Yangtze River in the Luoshan Hydrological Station and of the confined groundwater in the Honghu Lake area were used to estimate the aquifer diffusivity by using the power spectral method. The estimated aquifer diffusivity ranges from 1.6×104 to 8.7×105 m2/d with an average value of 1.8×105 m2/d， which is consistent with the results of 2.5×104-3.8×105 m2/d obtained from the transient pumping test and the inverse of a numerical model. Hence， the power spectral analysis is effective in the estimation of the aquifer diffusivity of confined aquifers.

Key words： spectral analysis; river-aquifer system; aquifer diffusivity; groundwater level; Honghu Lake area

河流和含水层之间的相互作用研究对于水文循环及河流附近生态环境建设具有重要意义。含水层对河水的响应程度与含水层的压力传导系数密切相关。压力传导系数理论上等于导水系数与贮水系数之比，是表征弹性动态条件下承压含水层中水头传递速度的参数[1-2]。压力传导系数是进行各种水文地质计算的基本物理参数，对于水资源的评价与合理开发利用、水污染的防治与预警、湿地生态环境保护等研究具有重要的理论和实践意义。

水文地質试验（如抽水试验、微水试验等）、数值模型反演是获取压力传导系数的常规方法[1-4]。通过观测地下水位，基于非稳定流地下水运动方程，水文地质试验依据特定的解析公式可以计算出含水层的渗透系数（导水系数）和贮水率（贮水系数），进而计算出压力传导系数。基于有限差分、有限元原理，建立地下水数值模型，以地下水位观测值与模拟值的差值平方和为目标函数，通过率定水文地质参数使目标函数达到最优，从而实现压力传导系数的反演。地下水位对河水位的响应程度与含水层的压力传导系数密切相关，因此理论上讲，根据地下水位对河水位的响应情况可以估算出含水层的压力传导系数。Hall等给出了河水位突变或连续变化情况下地下水位响应的解析解[5-7]，这些解析解可以实现含水层压力传导系数的估算，并已广泛应用于各种生产实践活动[8-11]。

近年来，国外学者提出了一种功率谱分析方法[12]，通过长期观测河水和河床不同埋深处的温度并计算其功率谱，成功估算了河床沉积物的有效热传导系数。由于热运移方程与承压地下水运动方程形式上较为相似[13]，因此采用功率谱方法有可能实现承压含水层压力传导系数的估算。笔者首先给出承压含水层压力传导系数的功率谱解析公式，然后以长江流域洪湖地区为例开展实例计算，并与非稳定流抽水试验和数值模型反演确定的压力传导系数进行了对比，以期为洪湖地区生态环境保护提供技术支持。

2 实例研究

2.1 研究区概况

洪湖地区位于湖北省东南部长江中游北岸三峡水库下游，是我国重要湿地之一。该地区属于典型的亚热带湿润季风气候区，雨季旱季分明，降水多集中于春夏两季，年平均降水量为1 000～1 300 mm，年平均蒸发量为1 300～1 400 mm[14-15]。

该地区水文地质条件相对简单，地下水主要以赋存于全新统冲、湖积多孔介质中的潜水和承压水的形式存在[14-15]，其中潜水主要赋存于浅部亚黏土、黏土、淤泥类土等细粒沉积物中，承压水主要赋存于深部较粗的粉细砂和砂砾层中。潜水含水层的含水性和透水性相对较弱且不均一，厚度为6～14 m;承压含水层分布较为广泛，厚度普遍大于20 m，顶板多被长江切穿，且与之有直接水力联系，是本次研究的对象。鉴于洪湖地区长江岸线相对平直，承压含水层厚度变化相对不大，可以近似使用图1所示的概念模型进行概化。

在石码头—小港布置了4眼承压含水层地下水动态长期观测孔[14-15]。这4眼地下水动态长期观测孔井深约35 m，揭露承压含水层顶板。石码头—小港剖面上游约25 km处的螺山水文站长期观测长江水位。地下水长期观测孔所记录的承压地下水位数据和螺山水文站所记录的长江水位数据是使用功率谱分析法估算承压含水层压力传导系数的重要资料。

2.2 数据及处理

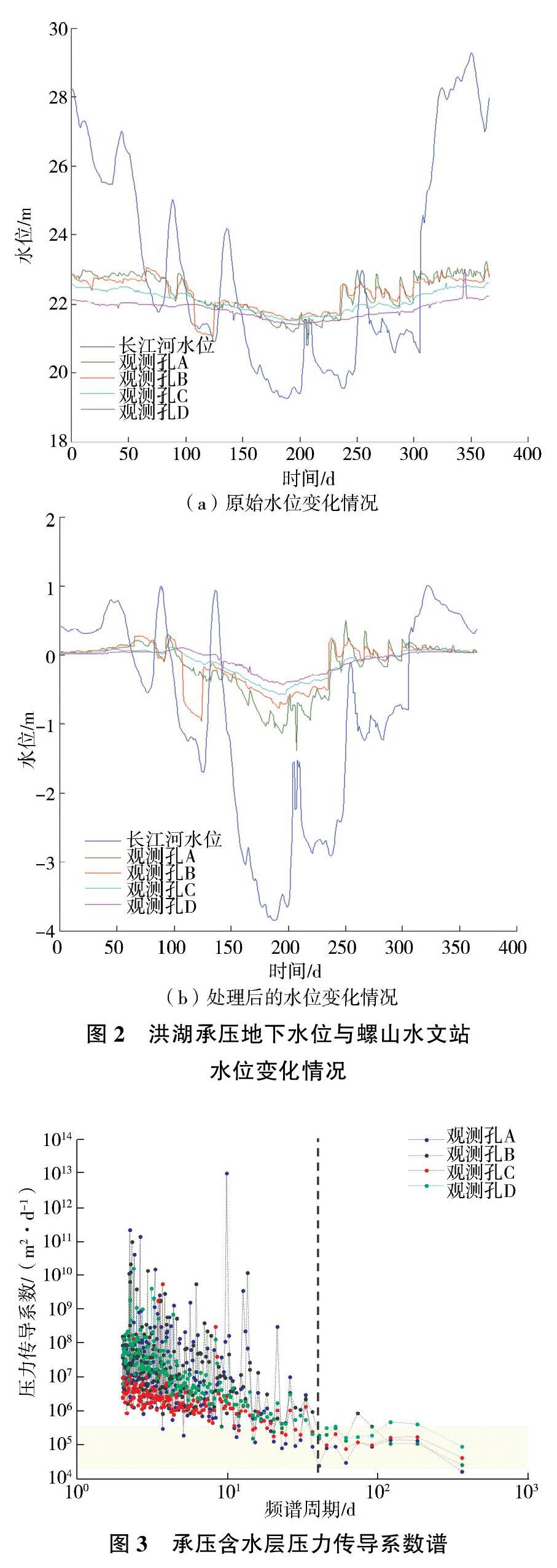
研究所采用的洪湖承压地下水位动态数据和螺山水文站长江水位数据以“d”为分辨率，时间域为一完整水文年，即从2011年7月1日到2012年6月30日，共计366 d，见图2（a）。洪湖承压地下水位与长江水位波动步调基本一致，显示出良好的相关性，表明两者存在较为紧密的水力联系。原始观测数据显示出较为显著的规律性和随机性波动。为消除规律性和随机性波动对功率谱分析方法计算结果的干扰，需对原始数据进行“去趋势化”和“汉宁窗”预处理。“去趋势化”是用来去除原始观测数据时间序列中的线性变化趋势，“汉宁窗”可以减少傅里叶变换过程中的频谱泄露，处理后的水位数据见图2（b）。

2.3 结果及分析

基于傅里叶变换，将经“去趋势化”和“汉宁窗”处理后的长江螺山水文站长江水位数据和4眼洪湖承压地下水位数据代入式（3），计算得到其对应的功率谱。将计算得到的功率谱及观测孔距离长江岸的垂向距离代入式（10），可绘制4眼地下水观测孔的压力传导系数谱，见图3。理论上讲，概念模型将含水层概化为均质各向同性体，压力传导系数为一常数，对应的功率谱曲线为一水平直线。实际上，由于实测地下水位受气象、地形、含水层非均质性等因素影响，因此功率谱曲线会发生系统或随机偏移。对于洪湖地区，4眼地下水长期观测孔的压力传导系数谱表现出较为一致的变化规律;在周期小于40 d时，压力传导系数波动强烈、不确定性大，主要受气象、上游三峡水库调蓄等因素引起的短期水位波动影响;在周期大于40 d时压力传导系数在105 m2/d附近，趋于稳定，综合反映了地下水位的长期波动。因此，使用功率谱方法估算得到洪湖承压含水层压力传导系数为1.6×104～8.7×105 m2/d，平均为1.8×105 m2/d。

图3中灰色阴影为前人使用非稳定流抽水试验或数值模型反演估算得到的压力传导系数的取值范围。对于洪湖石码头—小港地区，胡望斌等[14]使用解析解方法建立了反映长江水位变化与承压水动态的数学模型，模型中压力传导系数的取值为3.8×105 m2/d，是根据非稳定流抽水试验得出的。此外，徐亮等[15]使用Modflow建立了石码头—小港地下水数值模型，并使用实测水位数据进行了参数反演，结果表明洪湖承压含水层的渗透系数为20 m/d，弹性释水系数为0.000 13～0.000 80/m，换算得到的压力传导系数为2.5×104～1.5×105 m2/d。对比发现，前人使用不同方法估算得到的压力传导系数的取值范围与使用功率谱分析方法估算得到的结果有较好一致性，表明功率谱分析是估算承压含水层压力传导系数的有效方法。与非稳定流抽水试验和数值模型反演法相比，功率谱分析方法仅需借助前期观测得到的河水位和地下水位数据，便可估算得到河岸带尺度的含水层压力传导系数，具有良好的经济效益和应用价值，可为洪湖地区生态环境保护提供技术支持。

3 结 论

借鉴多孔介质热运移的相关研究成果，给出了承压含水层压力传导系数的功率谱解析公式，可以实现河流-含水层系统承压含水层压力传导系数的估算。洪湖地区承压地下水位与长江螺山水文站水位具有良好相關性，使用功率谱方法估算了承压含水层的压力传导系数，其与前人使用非稳定抽水试验和数值模型反演法得到的结果具有较好一致性。功率谱方法可以有效估算承压含水层的压力传导系数，可为洪湖地区生态环境保护提供技术支持。

参考文献：

[1] 陈崇希，林敏.地下水动力学[M].武汉：中国地质大学出版社，1999：1-30.

[2] 薛禹群，朱学愚，吴吉春.地下水动力学[M].北京：地质出版社，1997：5-26.

[3] 陈崇希.地下水流数值模拟理论方法及模型设计[M].北京：地质出版社，2014：8-55.

[4] 薛禹群，谢春红.地下水数值模拟[M].北京：科学出版社，2007：20-65.

[5] HALL F R， MOENCH A F. Application of the Convolution Equation to Stream-Aquifer Relationships[J]. Water Resources Research， 1972， 8（2）： 487-493.

[6] SINGH S K. Aquifer Response to Sinusoidal or Arbitrary Stage of Semi Pervious Stream[J]. Journal of Hydraulic Engineering， 2004， 130（11）： 1108-1118.

[7] 张蔚榛. 地下水非稳定流计算和地下水资源评价[M].北京：科学出版社，1983：214-292.

[8] HA K， KOH D C， YUM B W， et al. Estimation of Layered Aquifer Diffusivity and River Resistance Using Flood Wave Response Model[J]. Journal of Hydrology， 2007， 337（3）： 284-293.

[9] OH Y Y， HAMM S Y， HA K， et al. Characterizing the Impact of River Barrage Construction on Stream-Aquifer Interactions[J]. Water， 2016， 8（4）： 137.

[10] GIANNI G， RICHON J， PERROCHET P， et al. Rapid Identification of Transience in Streambed Conductance by Inversion of Floodwave Responses[J]. Water Resources Research， 2016， 52（4）： 2647-2658.

[11] 尹立河，张俊，王晓勇，等.基于地下水对洪水响应的含水层水力参数反演[J].人民黄河，2014，36（10）：58-60.

[12] WRMAN A， RIML J， SCHMADEL N， et al. Spectral Scaling of Heat Fluxes in Streambed Sediments[J]. Geophysical Research Letters， 2012， 39（23）： 234.

[13] CARSLAW H S， JAEGER J C. Conduction of Heat in Solids[M]. Oxford： Clarendon Press， 1959： 18-78.

[14] 胡望斌，王学雷，陈世俭.洪湖地区浅层承压水动态模拟研究[J].华中师范大学学报（自然科学版），2003，37（1）：119-122.

[15] 徐亮，陈世俭，向先富，等.基于Visual Modflow的洪湖石码头—小港剖面地下水数值模拟[J].华中师范大学学报（自然科学版），2008，42（2）：299-303.

【责任编辑 吕艳梅】