浅谈分类思想在初中几何入门中的应用

张晓会

数学思想方法，是对数学的本质认识，是数学学习的一种重要指导思想和方法。数学中的分类讨论思想，是一种重要的逻辑方法，它能使复杂的问题变得简单明了，还可以培养学生严密的数学逻辑思维和发散思维。

在初中平面几何中，分类思想也是比较常用的一种数学方法。那么平面几何问题一般在什么情况下需要进行分类讨论呢？又该怎么进行分类呢？通常在平面几何未给出相应图形，且关键词具有“模糊性”性时，往往就需要我们进行分类讨论。分类一般分为以下几步：首先，找出题目中的关键词;其次，画出相应图形;最后，分别按照图形进行分析作答。下面僅以几个题目为例进行说明。

解析：本题没有给出相应的图形，并且关键词是“点C在直线AB上”而不是“点C在线段AB上”，而直线是具有无限延伸性，所以C点可能在线段AB上，也可能在线段AB的延长线上。画出相应的图形（见下图）

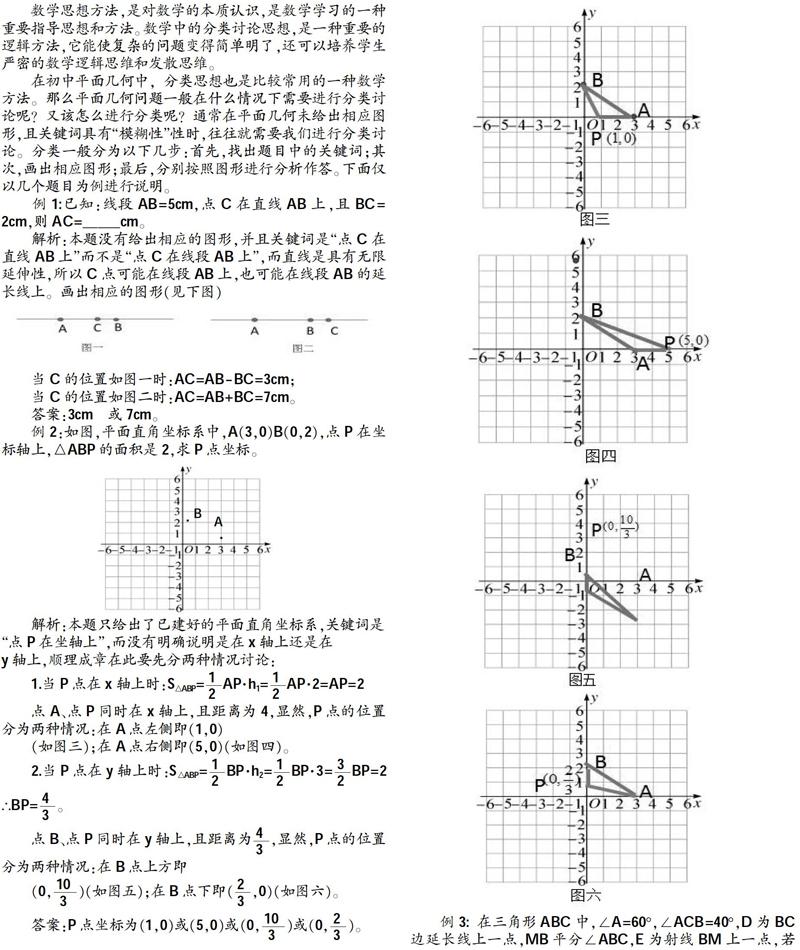
例2：如图，平面直角坐标系中，A（3，0）B（0，2），点P在坐标轴上，△ABP的面积是2，求P点坐标。

解析：本题只给出了已建好的平面直角坐标系，关键词是

“点P在坐轴上”，而没有明确说明是在x轴上还是在

y轴上，顺理成章在此要先分两种情况讨论：

点A、点P同时在x轴上，且距离为4，显然，P点的位置分为两种情况：在A点左侧即（1，0）

（如图三）;在A点右侧即（5，0）（如图四）。

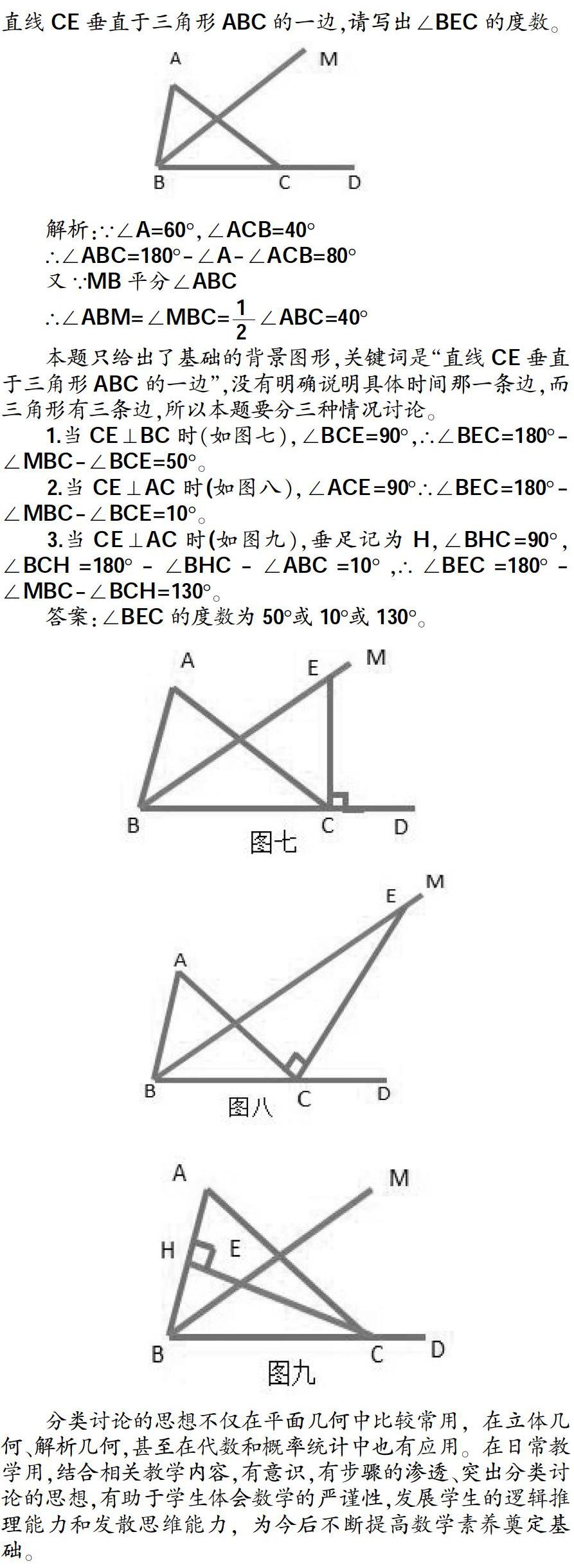
本题只给出了基础的背景图形，关键词是“直线CE垂直于三角形ABC的一边”，没有明确说明具体时间那一条边，而三角形有三条边，所以本题要分三种情况讨论。

分类讨论的思想不仅在平面几何中比较常用，在立体几何、解析几何，甚至在代数和概率统计中也有应用。在日常教学用，结合相关教学内容，有意识，有步骤的渗透、突出分类讨论的思想，有助于学生体会数学的严谨性，发展学生的逻辑推理能力和发散思维能力，为今后不断提高数学素养奠定基础。