沪港通开通对两地市场波动率的影响分析

[摘 要] 研究沪港通开通后上海、香港两地市场波动率的变化，选取沪港通开通前后半年的数据，利用加入虚拟变量的GARCH模型进行建模。由于沪市对数收益率序列自相关，所以建立ARMA模型得到均值方程，港市序列不自相关，设置均值为白噪声。建模后认为沪港通在一定置信水平下是证券市场波动率发生变化的原因，且沪港通开通使得沪港两市波动率增大，使市场更加活跃。然后进行格兰杰因果检验，证明到沪港两市间确有联动性，即港市引导沪市变动，港市变动是沪市变动的格兰杰原因，但沪市变动不是港市变动的格兰杰原因。

[关键词] 沪港通; 虚拟变量; ARMA模型; GARCH模型; 联动性

[DOI]10.13939/j.cnki.zgsc.2020.25.030

1 研究背景和意义

2014年11月17日，沪港股票市场交易互联互通机制（简称“沪港通”）试点在上海和香港同时进行，沪港通的开通是我国股票市场的重要举措，也是我国市场进一步对外开放的里程碑。沪港通包括沪股通和港股通两部分：其中沪股通是指投资者委托香港经纪商，经由香港联合交易所设立的证券交易公司，向上海证券交易所进行申报，买卖规定范围内的股票;港股通是指投资者委托内地证券公司，经由上海证券交易所设立的证券交易公司，向香港联合交易所进行申报，买卖规定范围内的股票。若不研究，则无法知晓该政策对证券市场波动率的影响，不利于政策的开展和实施，也不利于投资者进行投资决策。

在邹新阳和邓瑶（2018）[1]沪港通对沪港两市波动性的影响——基于GARCH模型的实证分析中利用沪港通开通四年的数据建立GARCH模型来进行影响分析，在金融领域不断发展和金融事件出现频率较高的情况下，长时间的数据反而不易证实政策对证券市场的影响，得到的结果很可能包含各种因素影响，而短时间的数据则减少了这一因素的影响，且本篇利用格兰杰因果检验证实了沪港两市之间的联动性。

2 数据处理

2.1 统计分析

利用网络数据库得到2014年5月17日至2015年5月17日上证180指数、恒生指数收盘价序列。检验收盘价序列的平稳性时得P>0.05，说明序列不稳定，采用收益率取对数的方法，得到上证对数收益率序列L和恒生对数收益率序列Q。

从上证180指数、恒生指数对数收益率序列的时间序列图中，可观察到对数收益率波动的“集群现象”[2]，即波动在一定时间段内较小或较大。得到对数收益率的统计量，如表1所示。

可观察到，上证180指数对数收益率序列偏度为0.570879，大于0说明序列分布有长的右拖尾，峰度为8.249203，高于正态分布值3。恒生指数对数收益率序列偏度为-0.295883，小于0说明序列分布有长的左拖尾，峰度为4.382327。说明两市对数收益率具有尖峰后尾的特征，结合J-B检验P值几乎为0，所以拒绝该对数收益率序列服从正态分布的假设。

2.2 序列自相关和偏自相关检验

在验证序列L、Q的平稳性时，检验得到序列L的t统计量的值为-15.85011，序列Q的t统计量的值为-14.56388，对应P值皆接近0，表明对数收益率序列L、Q平稳。

下面进行自相关检验，原假设E0：对数收益率序列不存在自相关性，备选假设E1：对数收益率序列存在自相关性。对序列L进行检验，有部分滞后项存在自相关性，所以进行ARMA模型的建立，经过对比选择，认为ARMA（5，4）最适，以下只对部分参数进行展示。

进行综合选择后，认为ARMA（5，4）最适合，得到序列L的均值方程：

yt=-0.003154-0.695743yt-4-0.170008yt-5+0.000206σt-0.105708σt-3+0.850772σt-4（2）

而序列Q检验自相关时P值显著大于0.05，接受原假设，认为序列Q在5%的错误率上不存在显著的相关性。所以序列Q的均值方程设为白噪音，为yt=μt+σt。

3 GARCH模型

在异方差检验中，AC和PAC值显著的不為0，且序列存在自相关，所以有ARCH效应。因此进行GARCH模型的建立，用加虚拟变量的GARCH模型分析沪港通开通后对波动率的影响。

上证180指数、恒生指数对数收益率序列GARCH模型方差方程：

σ2t=w+∑q1αiμ2t-i+∑p1βjσ2t-j+γdt（3）

为探索沪港通开通前后波动率变化情况，方便两阶段进行对比，加入虚拟变量DV[3]：dt

dt=0  ，当日期t < 2014/11/17

dt=1，日期t为其他值

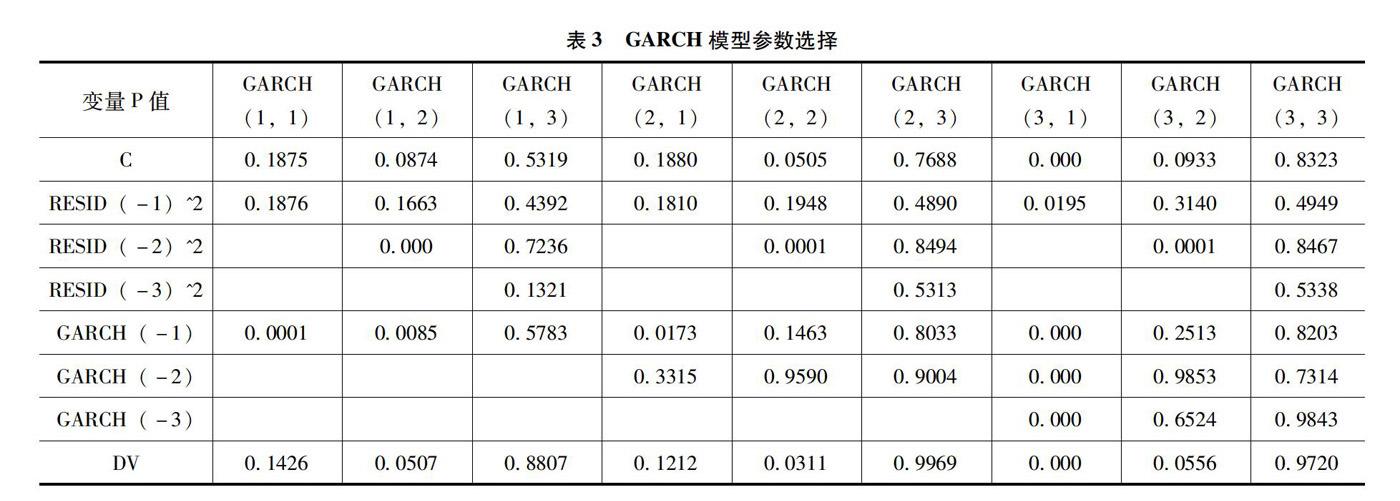
采取多个模型建模来寻找最适合的参数值。包含一至三阶共九个模型。现先进行上证180指数对数收益率序列的模型分析，结果显示GARCH（3，1）最适适合

由结果可得模型GARCH（3，1）最适合。在5%的错误率下认为沪港通开通前后有显著变化，即沪港通开通对序列有波动性影响。又虚拟变量DV值为6.00E-05 ，认为沪港通对沪市的影响是增大其波动的。结合实际情况，沪港通开通后，港市资金得以流入A股，使A股行情得到了新增资金的支持。再加上买卖方更加丰富，在多种因素趋势下使得沪市波动率增大。

恒生指数模型建立方法同，建立五阶及以下25个模型，分析结果可得GARCH（5，5）最适合。虚拟变量DV值为3.71E-05 ，综合上述认为沪港通开通对沪港两市皆有正面影响，增大了两市的波动率，使买卖方更加活跃和丰富。

4 模型验证

对建立的上证GARCH（3，1）、恒生GARCH（5，5）模型进行残差的ARCH效应检验，得到上证GARCH（3，1）对应P值为0.3301，恒生GARCH（5，5）对应P值为0.7218，均大于0.05，接受原假设，认为已无ARCH效应。

5 格兰杰因果关系检验

进行格兰杰因果关系检验的一个前提条件是时间序列必须具有平稳性，否则可能会出现虚假回归的情况。所以，利用上证指数对数收益率和恒生指数对数收益率进行格兰杰因果关系检验，探索两市之间的因果关系[4]。

可得到，在5%的水平下，上证指数不是恒生指数的格兰杰原因，而恒生指数是上证指数的格兰杰原因，认为港市的波动引导沪市的波动。

6 结论

根据实证结论，可以得到沪港通是引起沪港两市波动率产生变化的原因。沪港通开通前的波动率比开通后波动率小，认为沪港通开通后使沪港两市波动增大。在格兰杰因果检验中分析得到港市变动是沪市变动的格兰杰原因，但沪市变动不是港市变动的格兰杰原因。

对于证券市场来说，开通沪港通后两市波动变大，使市场更加活跃，资金更加流通，有利于证券市场发展。但是因为国际资金也会更加流通，市场上的套利行为可能引发比较剧烈的资本调动，只要存在资本利差就会发生这种情况，所以要构建完善的利率市场来避免这一风险。对于监管者来说，活跃的证券市场的监管任务难度将会提高，所以要对证券市场可能产生的风险和挑战进行监督和防范、加强宏观调控。因为港市变动引导沪市变动，所以可以让香港投资者的理性投资来促进沪市的发展。对于投资者来说，增加了投资的流通性，增加了投资渠道，外国投资者如果要购买A股，不再需要通过审批，只需要在香港市场开个户，即可参与交易。同时可分散投资风险，香港拥有大量来自世界各地优质的上市公司，包括一些海外跨国企业、香港和内地龙头企业等，更有一些内地稀缺的上市公司板块，沪港通的推出可帮助投资者实现资产的全球配置，分散投资风险。同时，两地互通的机制提高了信息的传递效率，投资者可以根据两地资产定价差异合理配置投资。

参考文献：

[1]邹新阳，邓瑶.沪港通对沪港两市波动性的影响——基于GARCH模型的实证分析[J].当代金融研究，2018（1）：57-66.

[2]王先宗.沪港通开通对上证A股指数波动的影响[J].中南财经政法大学研究生学报，2015（5）：60-66.

[3] WANG Y C，TSAI J J，LIN Y . The influence of Shanghai-Hong Kong stock connect on the mainland China and Hong Kong stock markets[J]. Social Science Electronic Publishing， 2017（10）.

[4]符明愷.沪港通背景下中国内地股市与香港股市联动性研究[D].重庆：重庆工商大学，2015.

[基金项目]乐山师范学院创新创业项目“沪港通开通后对证券市场的影响分析——以上海、香港证券市场为例”（项目编号：S201910649089）。

[作者简介]黄文杰（1999—），女，四川内江人，乐山师范学院数学与信息科学学院金融数学。