考虑健康状态的风电机组发电量预测模型
2020-10-12张子晗朱锦璇王远航
邓 超,张子晗,朱锦璇,吴 军,王远航
(1.华中科技大学 机械学院制造装备数字化国家工程中心,湖北 武汉 430074;2.华中科技大学 船舶与海洋工程学院,湖北 武汉 430074;3.工业和信息化部电子第五研究所,广东 广州 510610)
0 引言
风速的随机性和间歇性导致风电机组的输出功率具有很强的不确定性和波动性,随着风电场装机容量的增加和风电并网规模的增大,风电不确定性严重影响了电力系统的运行可靠性。精确合理的风力发电预测可以降低电力系统运营维护和调度控制规划的难度,从而减小风电并网对电力系统运行稳定性和并网经济性的影响。
现阶段风电功率预测方法主要分为物理模型方法和数据驱动方法。相比于使用大气动力学、风机参数、风电场地理环境建模的物理模型方法,数据驱动方法以数值天气预报(Numerical Weather Prediction,NWP)和风电场数据采集与监控(Supervisory Control And Data Acquisition,SCADA)系统为基础,通过统计学习方法、人工智能算法建立NWP数据与风电功率之间的非线性映射,实现发电量预测[1],解决了物理模型难以准确建立的问题。现有研究表明,数据驱动方法在进行超短期、短期风电功率预测时表现良好,但由于中长期风电功率预测对气象、地理因素依赖强,故单独采用数据驱动方法在进行中长期预测时实用性不强;而间接预测法,即结合风速和风电功率曲线(Wind Turbine Power Curve, WTPC)预测发电功率,在中长期风电功率预测中更有效。风电机组功率曲线是机组输出的有功功率与轮毂高度处风速之间的关系曲线,它反映了机组的发电性能;有效的功率曲线是风电发电量预测和风电场运行效益评估的重要工具。但目前风电功率曲线建模仅考虑风速因素与发电功率之间的映射关系[2],对影响风电机组发电功率的其他因素关注不足,如很少考虑风电机组健康状态对其发电能力的影响。然而,风电机组自身结构复杂,风速变化具有较强的随机性,机组在运行过程中受到不断变化的冲击载荷作用而导致性能劣化,故障频发,这必然造成机组发电能力下降。文献[3]利用气象数据和机组性能监测数据,采用支持向量回归方法预测风电机组的发电功率,结果表明综合考虑运行状态和气象信息的功率预测模型优于仅考虑气象信息的功率预测模型。因此,本文认为考虑风电机组健康状态来预测发电量能够提高预测准确性。
设备健康状态评估[4-7]利用状态监测技术评价设备当前的健康状况,预测其剩余使用寿命;对设备进行健康状态评估可以提前发现早期劣化故障、提前识别故障模式,进而在故障发生前安排必要的维修任务,从而减少设备主要部件故障和系统故障,提高维修效率、减少维修费用。风电机组是由叶轮、传动系统、变桨系统、偏航系统、电气系统等多个子系统组成的复杂设备[8],其健康状态的研究多从故障角度出发,主要包括故障树分析(Fault Tree Analysis,FTA)[9]、失效模式及后果分析(Failure Mode and Effect Analysis,FMEA)等方法[10],该类方法不能定量分析风电机组健康状态对发电功率的影响。风电机组风轮叶片、齿轮箱、转子、轴承、塔架等重要零部件的状态监测已经较为成熟[11-13],显然机组整体的健康状态应该依据这些状态监测数据来评估。由于风电机组健康状态指标难以选取,在多指标的情况下难以提取有效特征,从性能劣化角度评估机组整体健康状态的研究较少,但也逐渐引起了学者们的重视,肖运启等[14]依据模糊综合评价法,以风电机组多个性能的综合劣化度描述机组状态变迁,但模糊理论方法的权重规则建立较复杂且主观性较强,在实际工程应用中具有一定局限性。
隐Markov模型(Hidden Markov Model,HMM)是一种数据驱动统计模型,广泛用于语音识别和基因序列预测[15],近年来也被应用于设备健康诊断[16]。Liu等[17]根据单一传感器采集的轴承振动信号建立基于广义概率的HMM,诊断轴承故障类型及故障严重程度;刘勤明等[18]用最大似然线性回归方法融合处理多传感器信息,再以HMM预测液压泵的剩余使用寿命;Yu[19]利用基于HMM的马氏距离评估了轴承的健康状态等级;Du等[20]利HMM预测了油液剩余使用寿命;Wang等[21]利用卷积神经网络提取轴承振动信号特征后,用HMM进行故障分类,诊断轴承故障。本文引入组合权重描述机组多个健康观测序列之间的相关性,并采用改进的HMM来评估风电机组健康状态等级及各时刻机组处于某一级健康状态的概率。
综上所述,在预测风电机组发电量方面,现有研究几乎没有考虑机组健康状态对功率曲线的影响,致使预测误差加大;在评估风电机组健康状态方面,现有方法模糊性较强,不能定量评定机组整体健康状态对发电功率的影响。本文以综合考虑风能随机性、机组健康状态劣化的Markov性来预测机组长期发电量为目的,用改进的多观测序列HMM评估机组健康状态等级及各状态出现的概率,提出两种综合考虑风速与机组健康状态的动态风电功率曲线模型,对于风电场选址规划、运营调度具有一定的实际应用价值。
1 风电机组发电量预测框架
如图1所示,首先用改进的HMM来建立风电机组健康状态模型,主要包括为机组健康状态分级、确定健康状态观测指标、性能数据预处理、模型训练、健康状态评估5个步骤。将机组健康状态划分为5个等级,确立能反映机组健康状态的观测指标,并以此初始化模型参数。将机组多个性能观测指标的实测数据进行重采样和性能量化分级预处理,得到性能观测矩阵。用改进的Baulm-Weltch(B-W)算法和前向—后向算法训练性能观测矩阵,计算多观测序列HMM参数。再采用Viterbi算法预测健康状态序列,用前向—后向算法预测健康状态出现概率随时间变化的情况。

然后将健康状态劣化过程带入机组功率曲线,最终再结合风速模型建立考虑健康状态影响的发电量预测模型。用随机抽样一致性(RANdom SAmple Consensus, RANSAC)算法清洗风速与功率的异常数据,并基于比恩法建立机组不同健康状态等级的功率曲线Pi(v)。再利用健康状态劣化过程融合Pi(v),建立考虑健康状态的风电机组动态功率曲线P(t,v),最后结合基于Weibull分布的风速概率密度模型预测风电机组发电量。
2 基于HMM的风电机组健康状态评估
2.1 HMM基本框架
HMM是观测变量可见、状态变量隐含的双重随机过程[22]。隐藏过程是离散有限状态的齐次Markov链,其状态序列不可观察。下面将观测变量简称为观测值,状态变量简称为状态。

HMM的前向—后向算法还定义了前向概率αt(i)、后向概率βt(i),B-W算法还定义了联合概率变量ξt(i,j)、概率变量γt(i),如式(1)所示:
(1)
其中:1≤t≤T,1≤i≤N;αt(i)为模型λ给定时机组t时刻处于状态Si,观测序列为{o1,o2,…,ot}的概率;βt(i)为给定模型λ于t时刻处于状态Si,t时刻之后的观测序列为{ot,ot+1,…,oT}的概率;ξt(i,j)为给定模型λ和已知观测序列O时t时刻处于状态Si,且t+1时刻处于状态Sj的概率;γt(i)为给定模型λ和已知观测序列O时,设备t时刻处于状态Si的概率。
根据HMM,已知观测序列O时,可由前向—后向算法、B-W算法迭代训练出模型参数,再由Viterbi算法解码设备健康状态序列。
2.2 风电机组健康状态评估
利用HMM评估机组健康状态的过程中,机组健康状态对应模型的隐藏状态;机组多个性能的运行监测数据在经过预处理后,对应观测状态。用改进的B-W算法训练机组多个性能参数的运行监测数据,建立基于多观测序列HMM的健康状态模型,再利用Viterbi算法解码状态序列,用状态概率变量描述健康状态劣化规律。
2.2.1 健康状态分级
风电机组健康状态劣化的实质是其功能参数随时间连续偏移设定值直至机组失效,风电机组结构复杂,其劣化失效过程具有很强的模糊性和随机性,难以用多自变量函数来描述,因此本文采用分级的方式来描述其各个健康状态。
将风电机组健康状态划分为5个等级,即令N=5,记为S={S1,S2,S3,S4,S5},等级划分及物理意义描述如表1所示。

表1 风电机组健康状态等级划分
机组健康状态劣化过程在一次维修前是不可逆的,以如图2所示的离散型右转HMM作为其健康状态模型,表示机组初始状态为“健康”,在运行过程中最终将劣化至“危险”状态,并且在维修之前不再发生状态转移。
对于离散型右转HMM,有aij=0,j

2.2.2 确立健康状态观测指标
采用风电机组多个性能指标评估其健康状态,确立合理的观测指标是健康状态评估的基础。文献[3]对比了SCADA系统监测的机组各个性能参数与发电功率之间的皮尔逊相关系数,结果表明叶轮转速、齿轮箱油温、齿轮箱轴承温度、发电机转子转速、发电机转子温度和变流器温度等性能参数对机组的有功功率影响很大。
如表2所示,本文选取4个子系统的8个性能指标来评估健康状态,即令观测序列个数K=8,这8个指标的实测值越小,表明机组健康状态越优;当出现轴承磨损、发电机负荷过大等异常状况,监测的温度和振动偏差值则会增大,从而表明机组健康状态越差。

表2 风电机组健康状态观测指标
2.2.3 建立性能观测矩阵
为获取满足HMM训练条件的多观测序列,需要对实测数据进行预处理。
(1)实测数据重采样 实测性能数据数量有限,样本量不够,不能充分有效地训练基于改进HMM的健康状态模型,因此,为了充分训练模型使其更加准确有效,需要对实测数据进行重采样。分段三次Hermite插值多项式(Piecewise Cubic Hermite Interpolating Polynomial,PCHIP)兼具连续性和保形性,函数值和一次导数均在各插值节点连续,能够保持数据原有形状和增减性,不影响实测性能数据的准确性。利用PCHIP分别对各观测指标的实测数据进行重采样,以扩大样本容量便于HMM建模。
(2)性能量化分级 HMM可能的观测值个数M是有限正整数,而经重采样后的性能数据是连续的,直接将其作为观测值会给模型训练带来很大的困难,因此必须对其进行量化分级。性能量化分级分为两步:
1)用Lloyd算法优化聚类参数。令M=6,根据重采样数据,用Lloyd算法优化性能分级矩阵和聚类中心。
2)再依据优化后的聚类参数对重采样数据进行量化分级。以每个性能观测指标的6个聚类中心作为该指标量化分级的码本向量(codebook);以聚类中心从小到大的编号作为可能的观测值集合,记为U={1,2,3,4,5,6}。然后采用优化后的性能分级矩阵对数据进行量化编码,即将每个性能观测指标的重采样数据划分为6个类,再以每个重采样数据所属的类编号作为观测值,组成性能观测矩阵。
得到的性能观测矩阵为

2.2.4 多观测序列HMM训练
由于标准HMM仅限单观测序列输入,为了采用多性能指标来评估机组健康状态,需要对标准HMM进行改进,在无法判断各观测序列是否相互独立的情况下,需要引入组合权重来描述观测序列之间的相关性。对于性能观测矩阵O和初始模型参数λ=(π,A,B),有
(2)
性能观测矩阵的概率为单观测序列概率的加权之和:
(3)
其中,权重为:
(4)

(5)

(6)
(7)
(8)

2.2.5 健康状态评估
(1)健康状态序列预测
(2)健康状态概率预测
1≤t≤T-1;
(9)
t=T-1,T-2,…,1;
(10)
(11)
(12)
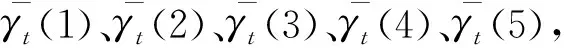
3 考虑健康状态的风电机组发电量预测
依据WTPC预测机组发电量时,在风速已知的情况下提高WTPC的准确性能够减小预测累计误差。本文利用考虑健康状态的风电机组动态功率曲线(Wind Turbine Dynamic Power Curve, WTDPC)预测机组的发电量。
3.1 考虑健康状态的机组动态功率曲线
机组各级健康状态下的功率曲线可以反映特定健康状态下机组发电功率与风速的关系。本文将健康状态评估的结果带入机组功率曲线,得到考虑健康状态的风电机组动态功率曲线。
3.1.1 机组各级健康状态下的功率曲线(WTPC)
2005年2月12日,经联合国教科文组织批准,雁荡山成为全球第一个以中生代火山岩地质地貌景观为主题的世界地质公园。公园总面积294.6平方千米,由三个园区组成:主园区雁荡山,位于乐清市境内,为中生代火山岩地质地貌景观;东园区为温岭市的长屿硐天古采石遗址和方山流纹岩台地地貌景观;西园区为永嘉县楠溪江河流地貌景观。
可靠的风电功率曲线是有效预测发电量的基础,学者们提出了一系列基于SCADA系统风速、功率数据的WTPC建模方法,其中比恩法(method of Bins)为国际电工委员会制定的标准方法,在实际工程中应用广泛[23-24]。然而,SCADA系统采集的数据包含通讯异常、传感器故障、数据传输噪声等导致的异常数据点,而RANSAC算法鲁棒性强,在异常数据点达总样本点50%时仍然能够有效进行多项式回归[25]。因此,本文先采用RANSAC算法对SCADA系统获得的数据进行数据清洗,以减小异常值对模型精度的影响;再采用过滤后的数据利用比恩法建立WTPC模型。建立各级健康状态下的功率曲线模型步骤如下:
(1)利用HMM评估t时段内机组健康状态qt。
(2)状态Si下的风速数据与功率数据的预处理。SCADA系统采集每10 min内的平均风速记为vn、平均功率记为pn,绘制(vn,pn)散点图。再利用RANSAC识别其中的异常值,并剔除这些外点(outlier),从而筛选出符合模型特征的内点(inlier),即(v*,p*),为WTPC建模做准备。

(13)
(14)

3.1.2 机组动态功率曲线(WTDPC)
本文2.2.5节给出了两种形式的健康状态评估结果,相对应地有两种形式的动态功率曲线。
(1)考虑健康状态等级序列的WTDPC,认为随着时间的增加,机组健康状态、发电能力发生“等级下降”,当t时刻的机组健康状态qt=Si,动态功率曲线为
P(t,v)=Pi(v)(qt=Si,i=1,2,…,5)。
(15)

(16)
3.2 机组发电量预测
风电机组发电量W(kW·h)常规计算方法为

(17)
式中:T为发电时间(单位:h);vmax为机组切出风速(单位:m/s)、vmin为切入风速(单位:m/s);P(v)为机组功率曲线,其功率单位为kW;f(v)为基于双参数威布尔分布(WBL-2)的机组风轮轮毂高度风速的概率密度函数(Probability Density Function,PDF)[26]:
(18)
式中:v为风速(单位:m/s);η为形状参数(无量纲);c为尺度参数(单位:m/s)。
因此,考虑健康状态的风电机组动态功率曲线预测机组发电量为
(19)
4 工程实例
为验证本文所提风电机组发电量预测方法的有效性,以SL2000/100双馈异步风电机组为例进行验算,机组性能数据和风速数据均来自SCADA系统的监测数据;其中机组实际发电量已依据调度日志按月进行折算,整个健康状态评估过程中没有进行机组大修。
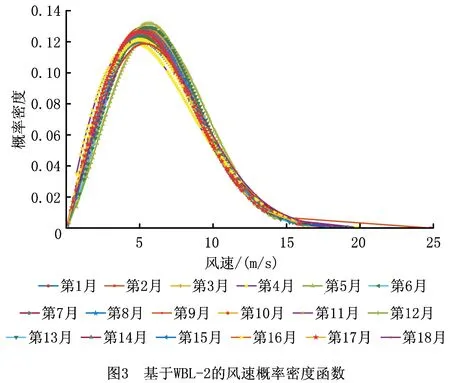
根据风速数据,用最大似然估计法计算式(18)中的参数,得到机组风轮轮毂高度的18个月的风速概率密度函数(如图3)。
4.1 机组健康状态评估
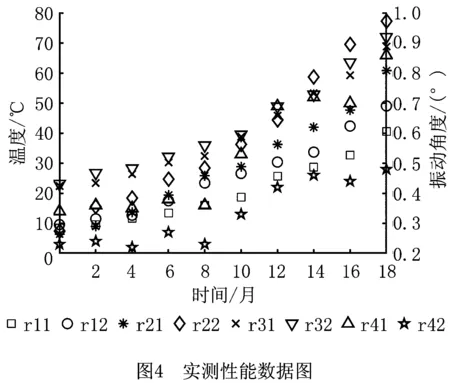
机组从投入使用至故障停机期间,由表2选定的机组8项健康状态观测指标的性能数据如图4所示,图中数据均为风速为6.0 m/s时采集后求得平均值。按2.2.3节方法进行性能数据预处理。用PCHIP重采样后得到如图5所示的性能数据。再对重采样数据进行性能量化分级,得到性能观测矩阵(如图6)。






利用2.2.5节方法评估机组健康状态,得到机组健康状态序列(图7a)和健康状态概率(图7b)。
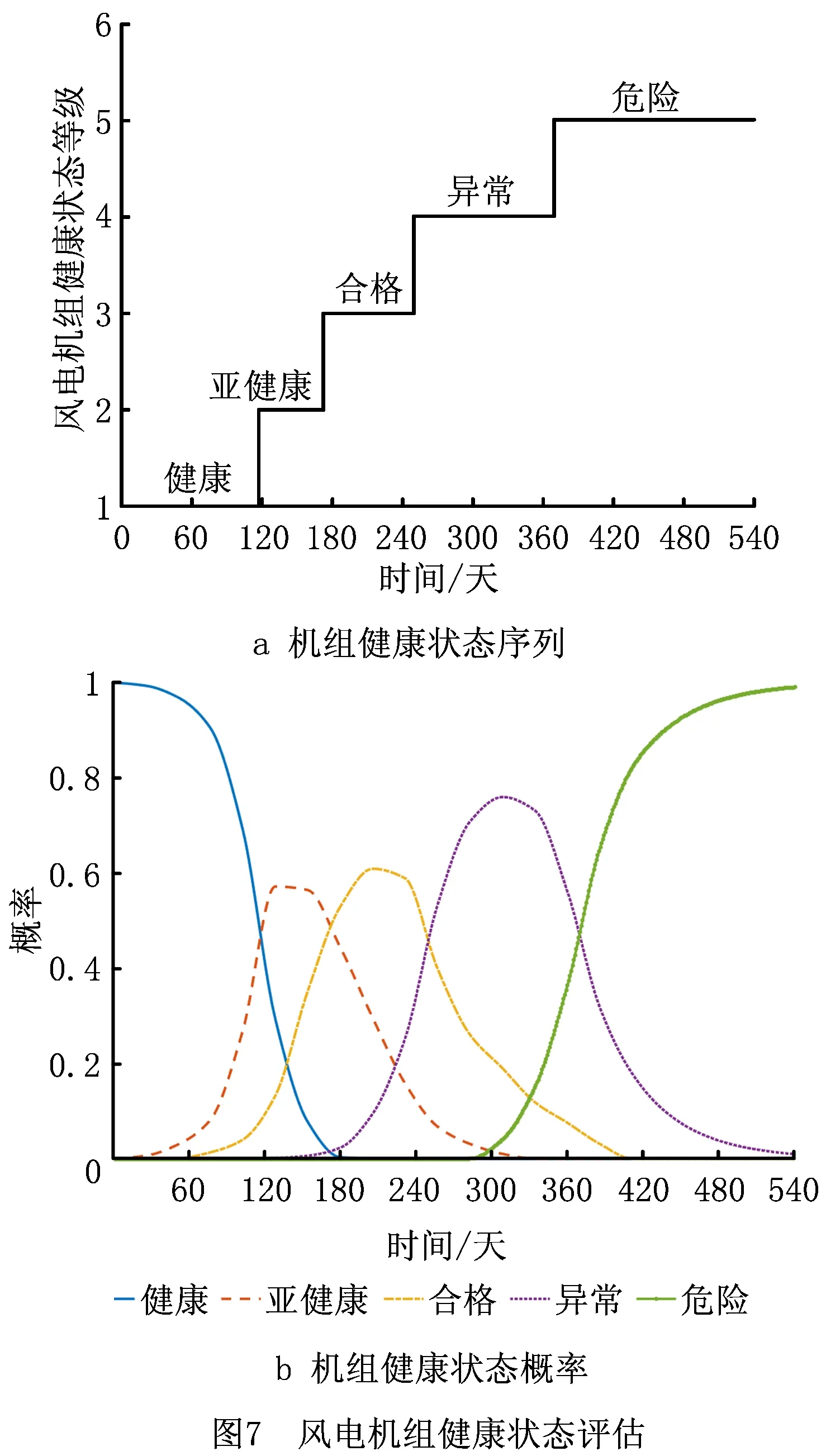
由图7a可知,机组初始状态为S1,此后机组一直发生性能劣化,在第117天跳转为S2状态;对应地,由图7b中可看出机组初始时刻处于S1的概率为1,运行过程中S1的概率不断减小而S2概率有所上升,并在第117天超过了S1的概率。整个运行过程中机组健康状态劣化经历5个阶段,与实际情况一致。
4.2 WTPC建模
由机组技术手册知其切入风速为3 m/s,额定风速为12.5 m/s,切出风速为25 m/s,额定功率为2 Mw。机组运行过程中机械损耗会导致机组发电能力下降,这使厂家给定的理论功率曲线不再适用,故需要建立实际功率曲线模型。以亚健康状态为例说明各级健康状态下WTPC建模过程。先剔除亚健康状态机组3天的每10 min内的平均风速、平均功率数据点(vij,pij)中的空值和明显错误值,并利用RANSAC对散点进行多项式回归,设置容错阈值为40、置信度为95%,结果如图8a所示,内点数据占全部数据点的59.07%;再用比恩法建立内点的WTPC,如图8b所示,采用RANSAC数据清洗后的功率曲线更平滑。

按照以上方法得到机组5种健康状态时的风电功率曲线(图9),可知相同风速时不同健康状态的机组发电功率有差异,且均不同于厂家所给理论功率值。在最大风能捕获区(v=3~10 m/s)差异较小,而在恒转矩区(v=10~13 m/s)和恒功率区(v=13~25 m/s)差异较大。

4.3 WTDPC建模
为验证本文方法的有效性,建立3种风电机组动态功率曲线模型。模型1为不考虑健康状态劣化的WTDPC(如图10a),机组运行过程中发电能力不发生下降;模型2为由式(15)得出的考虑健康状态等级序列的WTDPC(如图10b),随着运行时间增长机组健康状态等级下降,发电能力也呈现明显分层现象;模型3为由式(16)得出的考虑健康状态劣化概率的WTDPC(如图10c),机组各等级健康状态出现的概率随着运行时间增长不断变化,发电能力无明显分层,而是呈现连续性的下降。
在3种WTDPC模型中分别取10种风速,对比风速相同时发电功率在不同功率模型下的差异(如图11)。


由图11可知,风速仍是影响机组发电功率大小的最主要因素;但风速情况相同时,随着机组运行时间增长,机组健康状态的劣化引起了发电能力的下降。模型2、模型3的机组18个月内发电功率随时间变化趋势非常接近。
4.4 发电量预测及结果分析
按照3.2节方法预测机组发电量,表4为月发电量实际值与3种模型预测值的对比情况。其中准确率计算公式为:


表4 月发电量实际值与预测值对比
根据表4,绘制月发电量预测结果(图12a)与月发电量预测结果准确率(图12b)来比较3种模型。
由图12a可知,在机组投入稳定运行的前3个月,3种模型的发电量预测结果基本一致,而此后由于机组性能劣化,模型2、模型3的预测值与模型1的差异逐渐增大。但风速仍然是影响机组发电功率大小的最主要因素,例如机组第5个月处于“亚健康”状态,第16个月处于“危险”状态,但由于前者风资源不足而后者风资源充足,尽管第16个月机组健康状态较差但发电量却更多。
由图12b可知,模型2、模型3的月发电量预测准确率较模型1要高,说明考虑健康状态的发电量预测模型优于不考虑健康状态的预测模型。模型2与模型3的准确率基本一致,从而验证了多离散状态健康预测模型的科学性;模型3实际上是机组发电能力无限离散劣化的例子,反映了机组性能逐渐劣化时发电能力呈现连续性下降的特征。同时,模型的准确率在时间尺度上没有明显的规律性,这是由于实际发电量也受风速、风向、空气密度、调度规划控制等不确定性因素的影响。
5 结束语

准确的风电机组发电量预测是有效进行风电系统调度与规划的基础,提高其精度能够减小风电并网对电力系统稳定性和经济性的影响,而以往的发电量预测方法很少考虑风电机组健康状态的影响。本文以双馈异步风电机组为研究对象,在分析机组健康状态对发电功率影响的基础上,建立考虑健康状态的风电机组发电量预测模型。提出基于多观测序列HMM的大型风电机组健康状态评估方法,该方法不同于以往直接假定各观测序列独立的方法,而是引入组合权重描述观测序列之间的相关性,最终以健康状态等级序列、健康状态劣化概率表示机组健康状态随时间的变迁。依据以上HMM,提出两种考虑机组健康状态的动态功率曲线模型和发电量预测模型,不同于以往只包含气象信息的风电功率曲线,本文的动态功率曲线中发电功率还随另一自变量——时间而变化,时间序列中包含了机组健康状态劣化信息。相比于现有功率曲线模型,该模型能反映风速、健康状态对机组发电功率的共同影响,这为风电机组发电功率、发电量预测的研究提供了新的方法和思路。
风电机组健康状态评估、发电量预测涵盖内容广,涉及技术难点多,机组健康状态劣化是一个长期的过程,但风速变化时间尺度短,将现有的短期风速预测方法与本文所提出的中长期发电量预测相结合具有重要意义。
