SMV静态混合器的几何结构对流场参数的影响

崔 艳，于建成，段彩云，孙 光

(1.山东商务职业学院，山东 烟台 264670；2.山东大学 机械学院，山东 济南 250061)

SMV型静态混合器(Static Mixer) 是一种应用范围较为广泛的静态混合器，在石油化工、药品、化妆品等领域的混合、萃取、热交换、分散、溶解等工艺过程中都能用到[1]。

SMV静态混合器是众多静态混合器SK、SV、SX、SH、SL、SMV 及SMX 等多种类型中的一种[2-3]，其结构特性，流场特性，国内外均有相关的实验研究和模拟研究[4-5]。许多文献预测了SMV 型静态混合器中的湍流流动[6-8]，沈阳化工大学张春梅，王泽斌等针对标准SMV静态混合器做了实验和模拟[9-10]，南京工业大学的樊水冲[11-12]等人模拟了SMV 型静态混合器内的流场，计算了压力降,分析了其强化传热的特性。海军工程大学的赵建华[13]分析了SMV型静态混合器的流场，及其对湍动能和离散相分散性的作用。张国锋等[14]对静态混合器使用数值模拟进行结构优化。

以上文献都是以标准SMV混合器为研究对象，其几何结构波纹板折弯角φ和波纹板交错角θ均为90°，然而SMV混合器的层板交角和折弯角的不同必然对其流场参数具有影响。

本文采用CFD方法对SMV静态混合器的流动状况进行模拟，通过调整静态混合器的几何结构，研究了包括压降、湍动能等流场参数的变化情况。

1 物理模型以及数值模拟方法

1.1 物理模型

本文在标准SMV型静态混合器的基础上对SMV静态混合器的几个主要参数进行研究：

单元长度L：混合单元长度；

折弯角度φ：混合单元的波纹板的折弯角度；

交错角度θ ：SMV静态混合器波纹板叠加的交错角度。

图1 SMV静态混合器几何参数

图1所示即为SMV静态混合器的几何参数以及混合器单元组装结构参数。

本文模拟的其它实验条件定为管道长度M=0.08m，SMV混合单元为4层，混合单元直径d=0.01m。

SMV静态混合器的几何参数进行分析的具体数值如下表1所示：

表1 SMV静态混合器模拟条件参数

1.2 数学模型

为便于分析计算，通常对计算模型作如下简化假设：(1)流体连续性为常数不随时间变化而变化；(2)混合器内的温度是恒定的；(3)不考虑重力影响；(4)流体是粘度视为恒定，不考虑压力影响。

1.3 网格划分

本文网格使用Solidworks建模，导入ICEM生成，由于混合器结构复杂，使用非结构四面体网格进行划分。网格大小选用 0.3 mm，对应的网格数量为3×106。

图2 混合单元网格划分图

1.4 湍流模型

该模型采用计算流体力学软件 Fluent进行数值模拟计算。因为该管道内部流动为完全湍流，并且依据文献[10]结论，采用Realizable 模型。

流体介质为常温20℃水。设定边界条件为速度进口，压力出口，壁面为光滑壁面。

表2 流体参数以及流场系数

1.5 数值模拟验证与网格无关性验证

为验证数值模拟方法的正确性，其模拟结果与本文的实验装置结果进行对比。实验平台如图所示。

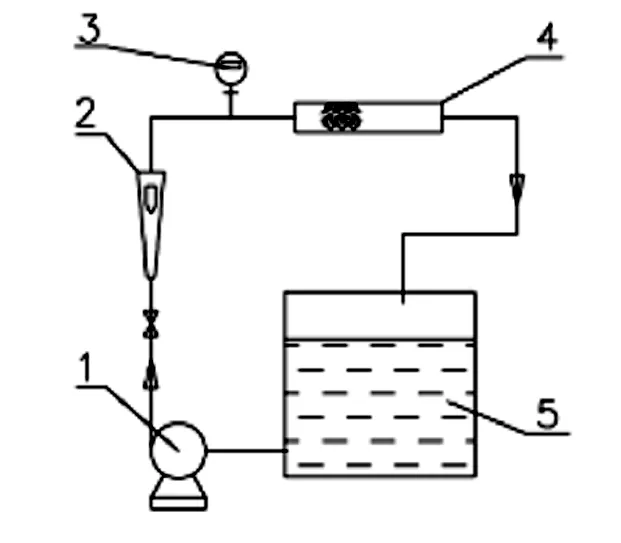
1.计量水泵;2.流量计;3.压力传感器;4.静态混合器管道;5.水箱

图3 实验装置简图

实验装置使用计量泵来定量控制流量，保证管道内部流速为2m·s-1，静态混合器采用标准SMV静态混合器(折弯角度φ=90°，交错角θ=90°)，长度分别为0.005m，0.01m，0.015m，0.02m。实验装置对压降进行数据采集。

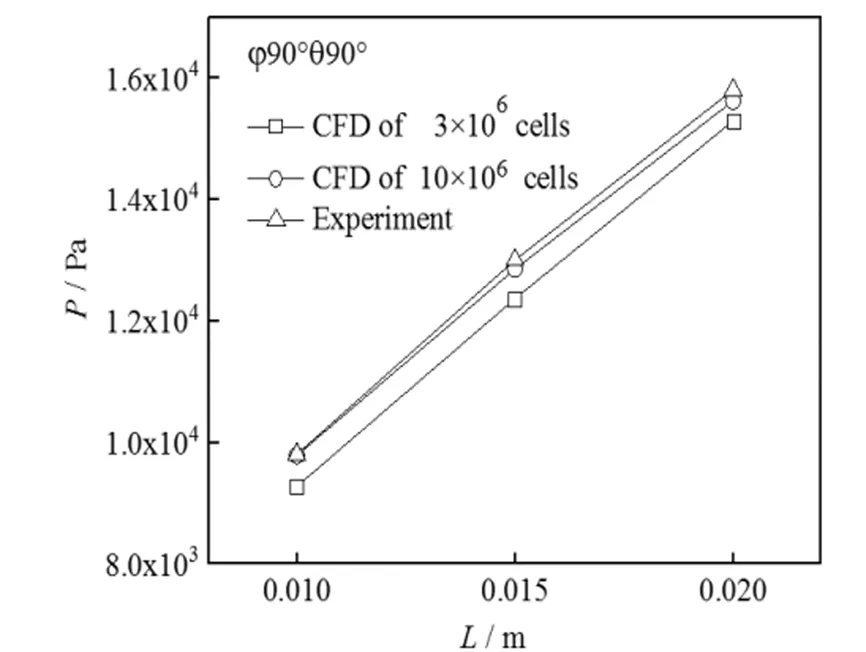
图4 模拟结果与实验结果对比

数值模拟采用相同参数，并对网格划分为3×106和10×106两种网格数量，所得结果如图所示，可以看出模拟结果压降与实验值相比较差别不大，并且网格数量为10×106的结果更接近实验，网格数量为3×106的结果与实验比较，误差在5%以内，综合考虑两种网格的计算时间，最终选择划分网格数量为3×106进行模拟。

2 计算结果与分析

模拟实验分别对混合单元长度L、折弯角度φ、等参数进行变化，对其变化的条件算例进行模拟，为了考察混合单元的湍动能，选取进出口压降( pressure drop) ΔP混合单元的耗能以及阻力的特征参数，选取管道平均湍动能(Turbulent Kinetic Energy)TKE作为混合单元对流场湍流强度的对应参数。并定义一个参数将湍动能压力比(TKE/ΔP)B，作为混合单元湍动能效率的参数进行分析。

2.1 混合单元长度

本结果是在一个单元的情况下，固定交错角度θ=90°，折弯角度φ分别为60°，90°，120°的混合单元，以长度L作为变化参数，对流场参数的影响。根据充满圆管的牛顿流体流动压力降范宁(fanning)公式。

(3)

ΔP，压力降，Pa； ρ，流体密度，kg˙m3；u，流体平均速度，m˙s-1；g，重力加速度，m˙s-2；L，管道长度或者混合器长度，m，；D，管道内径，m； λ，管壁摩擦系数

对于混合单元具有异形断面的管路压力损失，需要计算水力直径dh，水力直径dh定义为四倍的空隙体积与浸润面积的比值，即：

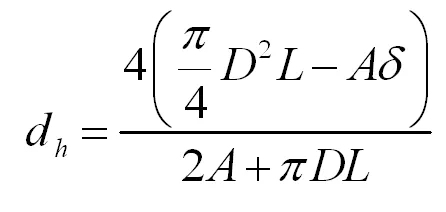
(4)

式中A为波纹板的单面面积，δ为波纹板厚度，由此可得混合单元的压降公式：

(5)

按照公式进行计算，发现在相同的折弯角度下，其水力直径是相同的，对应的雷诺数也相同，因此可以判断，在固定交错角度θ，折弯角度θ的情况下，压降只是长度的函数，这与相关文献[14]一致。

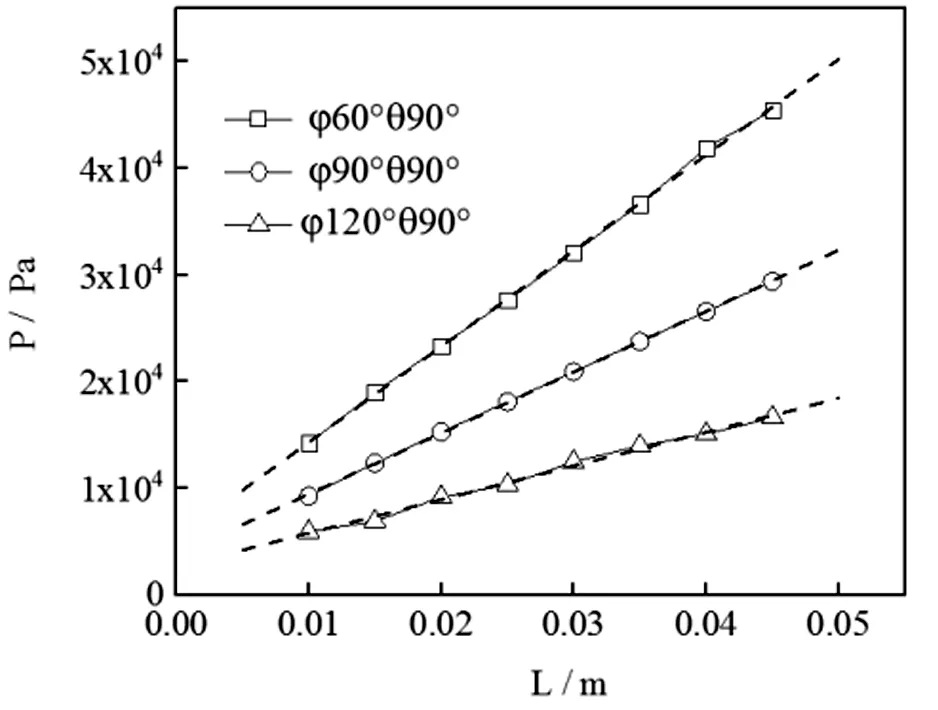
图5 长度不同对应的压降变化

图6 长度不同对应的管道

湍动能变化曲线与云图

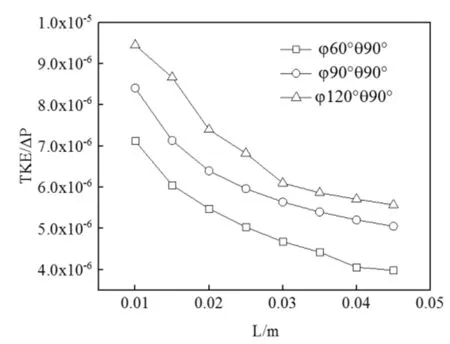
图7 长度不同对应的湍动能压力比变化

图中虚线为拟合函数。图5所示为随着单元长度的增加，管道湍动能TKE也随之增加，相比较压降ΔP的增加幅度，其斜率有所降低。

本文根据模拟的数据进行数据拟合，得出压降和湍动能与长度的函数关系式

从拟合公式观察，不同的折弯角度具有不同的λ和λα值，λ可以定义为混合单元阻力系数，λα可以理解为管道内壁的附加阻力。λt是混合单元的湍动能系数，λl管道附加湍动能。

折弯角度越小，其混合单元的阻力越大，这是可以简单理解的，折弯角度变小必然导致混合单元内部通道数增加，通道也更复杂，其湍动能也必然增加。

但结合图6可以看出，湍动能压力比B的变化，折弯角度的增加，其湍动能的效率减小；而伴随长度增加而湍动能效率也降低，因此，增加混合单元长度，会同时使湍动能和阻力增加，但是阻力增幅要比湍动能更大，导致比值B会减小。

2.2 折弯角度

波纹板的折弯角度φ也是一个重要参数，在交错角度为θ=90°，单元长度L=0.01m，的条件下，其对于流体的影响如下图所示。

图8 折弯角度不同对应的压降变化

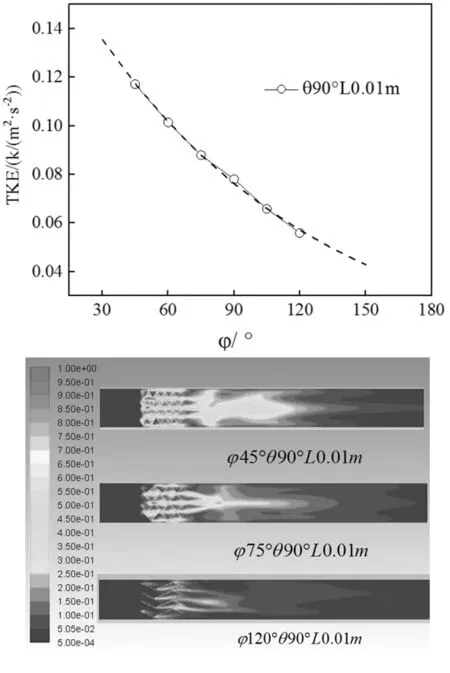
图9 折弯角度不同对应的管道湍动能变化曲线与云图

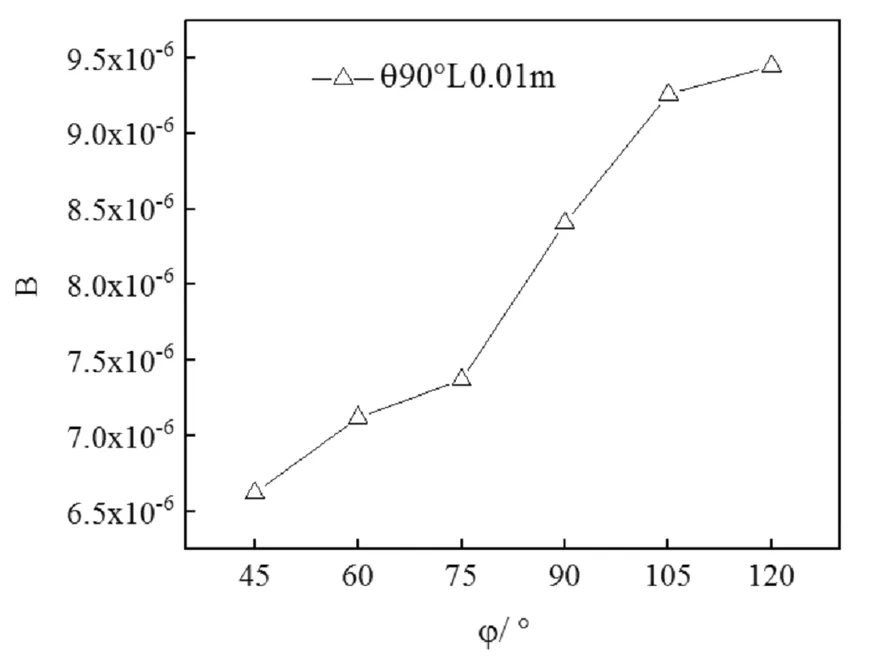
图10 折弯角度不同对应的湍动能压力比变化

图中虚线为拟合函数。综合分析图7～图9，可以看出，折弯角度 越大，其压降越小，折弯角度 越大，其波纹板的越趋近于平整，对于流体产生的阻力自然会下降。

观察其对于湍动能TKE也是同样的影响趋势。湍动能云图也可以看出折弯角度越小，其流场越复杂，产生的湍动效果也很明显。

由于折弯角度的不同，导致水力直径、雷诺数、阻力系数均有变化，文章对此进行简化分析，仅做折弯角度与压降和湍动能的关系分析。

折弯角度所引起的变化，文章做了函数拟合

相比较长度引起的变化，折弯角度与压降和湍动能更近似于指数函数，但是对于湍动能压力比B的影响，结果由两个方程相比，也是一个指数函数。

可见，折弯角度越小增加了湍动能，但是也同时增加了混合单元的面积，因此管道压降不仅仅是湍动能还有管道阻力的增加。

3 结论

文章通过数值模拟研究了SMV混合单元的管道流场情况，对几个主要参数进行了系统分析，证明SMV静态混合器可以通过改变几何结构使性能提升。具体结论如下。

(1)混合单元长度与湍动能和压降成线型正比关系。增加混合单元长度，会同时使湍动能和阻力增加，但是阻力增幅要比湍动能更大，导致比值B会减小。

(2)折弯角度越小增加了湍动能，但是也同时增加了混合单元的面积，因此管道压降不仅仅是湍动能还有管道阻力的增加。但在混合单元制造过程中，过小的折弯角度会增加冲压工艺的难度，因此，在实际加工中，应当尽量选取适合加工工艺的最小折弯角度。