交通和运行荷载耦合作用下管道承插口力学响应研究

王复明，何 航，方宏远，李 斌

(1．郑州大学 水利科学与工程学院，河南 郑州 450001；2.郑州大学 重大基础设施检测修复技术国家地方联合工程实验室，河南 郑州 450001；3.郑州大学 水利与交通基础设施安全防护河南省协同创新中心,河南 郑州 450001；4.南方工程检测修复技术研究院,广东 惠州 516029)

0 引言

承插式排水管道作为城市基础设施的重要组成部分，在保障居民日常生活中起到了举足轻重的作用。但由于管道埋设环境复杂，常年受上覆荷载(交通、土压)、流体荷载及管周环境的耦合影响，管节接头处可能出现破坏，导致管道渗漏等问题出现，严重的甚至会造成道路坍塌等安全事故[1-2]。因此研究埋地管道承插口在多场荷载耦合作用下的受力和变形特征极有必要。

Xu等[1]采用三维数值方法，研究了交通荷载作用下带橡胶圈和承插口的大管径钢筋混凝土管道的纵向响应，分析了管节的力学性能和变形。Buco等[2]开发了一种用于测试各种载荷条件下管道接头性能的装置，并基于试验结果提出了一个管道接头流变双线性模型。王复明等[3]通过Abaqus建立了带有承插口的混凝土管道模型，并考虑了橡胶圈的影响，研究了脉冲荷载作用下排水管道的动力响应，分析了承插口的力学特性。

作用在管道上的外荷载除了上覆土压力和交通荷载外，还包括管内流体和管道间的流固耦合(FSI)，Xu等[4]利用ANSYS Workbench平台进行流固耦合数值模拟，研究了L型热管的传热和介质流动特性，分析对比了不同工况下流场的压力和温度以及管道肘部结构的温度和应力，比较了耦合和非耦合载荷下管网的力学性能。张志鑫等[5]通过MpCCI对三通管接头进行了流固耦合、流固热耦合数值仿真，分析了三通管的Mises应力和位移，并对比了流固耦合和流固热耦合结果。俞树荣等[6]以流固耦合理论为基础，在ANSYS Workbench平台对弯曲输流管道内流体动力学和固体运动模型进行建模，并进行了双向、单向流固耦合分析和模态分析，研究了脉动压力、壁厚和管径等因素对其的影响。

笔者在前人研究的基础上，利用Abaqus和Fluent软件建立了管道结构和流体模型，并基于MpCCI软件平台模拟了多物理场耦合作用下管道的运行状态，计算分析了流场流量、荷载大小和荷载作用位置对管道承插口力学性能和竖向变形的影响。

1 三维数值仿真模型

1.1 结构模型

在Abaqus中建立了三维混凝土管道模型和路面结构模型，模型整体取长×宽×高=12 m×8 m×7 m。混凝土管道埋深1.0 m，直径800 mm，壁厚92 mm，每节长度2 m，如图1所示，管道材料为C30混凝土，采用Lee等[7]提出的混凝土损伤塑性模型。道路结构分为路面和路基，厚度分别为0.25 m和6.75 m，路面采用线弹性本构，路基采用摩尔库伦弹塑性本构。在管土的交界面处设置摩擦接触，切向为罚接触，法向为硬接触。管土接触面摩擦系数[3]为：

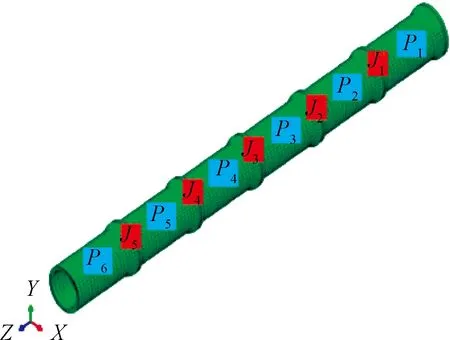
图1 管道有限元模型Figure 1 Finite element model of pipeline

(1)

式中：A、B、C是拟合的常数，取决于土体的不排水抗剪强度，分别取0.756、0.461、0.204。

结构场的边界条件：约束模型底面3个方向的位移自由度和模型4个侧面法向位移自由度。

相关材料参数如表1所示，整体结构网格剖分如图2所示。

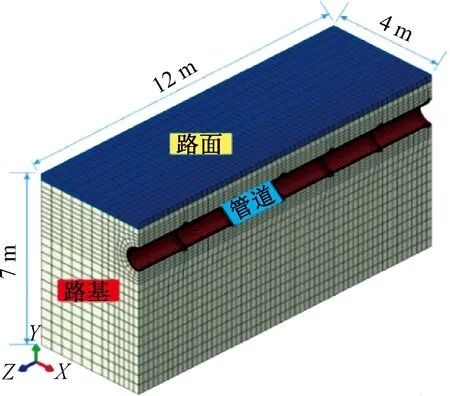
图2 整体结构网格剖分Figure 2 Mesh of the overall structure

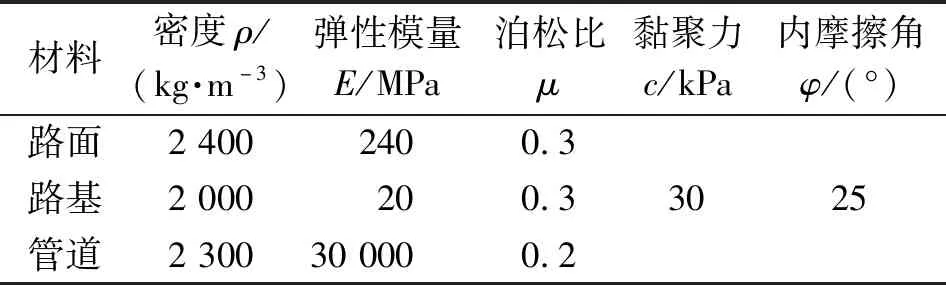
表1 材料参数Table 1 Material parameters

1.2 橡胶圈模型

管节承插口选用橡胶圈作为密封材料，参考相关规范将橡胶圈材料看成是THA55和THA86两种材料的组合体。张世杰[8]研究发现，Mooney-Rivlin应变能函数对橡胶圈材料力学试验的拟合度较高，且在工程应用中更为广泛。其应变能函数方程为：

(2)

式中：C01和C10是Mooney-Rivlin模型的材料参数；D1为常数。笔者所采用的Mooney-Rivlin应变能函数的相关参数如表2所示。

在橡胶圈内壁和插口外壁、橡胶圈外壁与承口内壁设置接触单元[1，9]，切向采用罚函数，摩擦系数为0.2，法向采用硬接触。

1.3 交通荷载

落锤式弯沉仪(FWD)是目前公路检测领域中广泛使用的检测手段，能够较好地模拟实际行车荷载。本次模拟采用落锤式弯沉仪的脉冲荷载实测曲线，作用面积为0.4 m×0.2 m，轮距为1.2 m，分别作用在J3的正上方和两侧，采用3种幅值大小(0.5 MPa、0.7 MPa、1.0 MPa)。荷载曲线如图3所示。

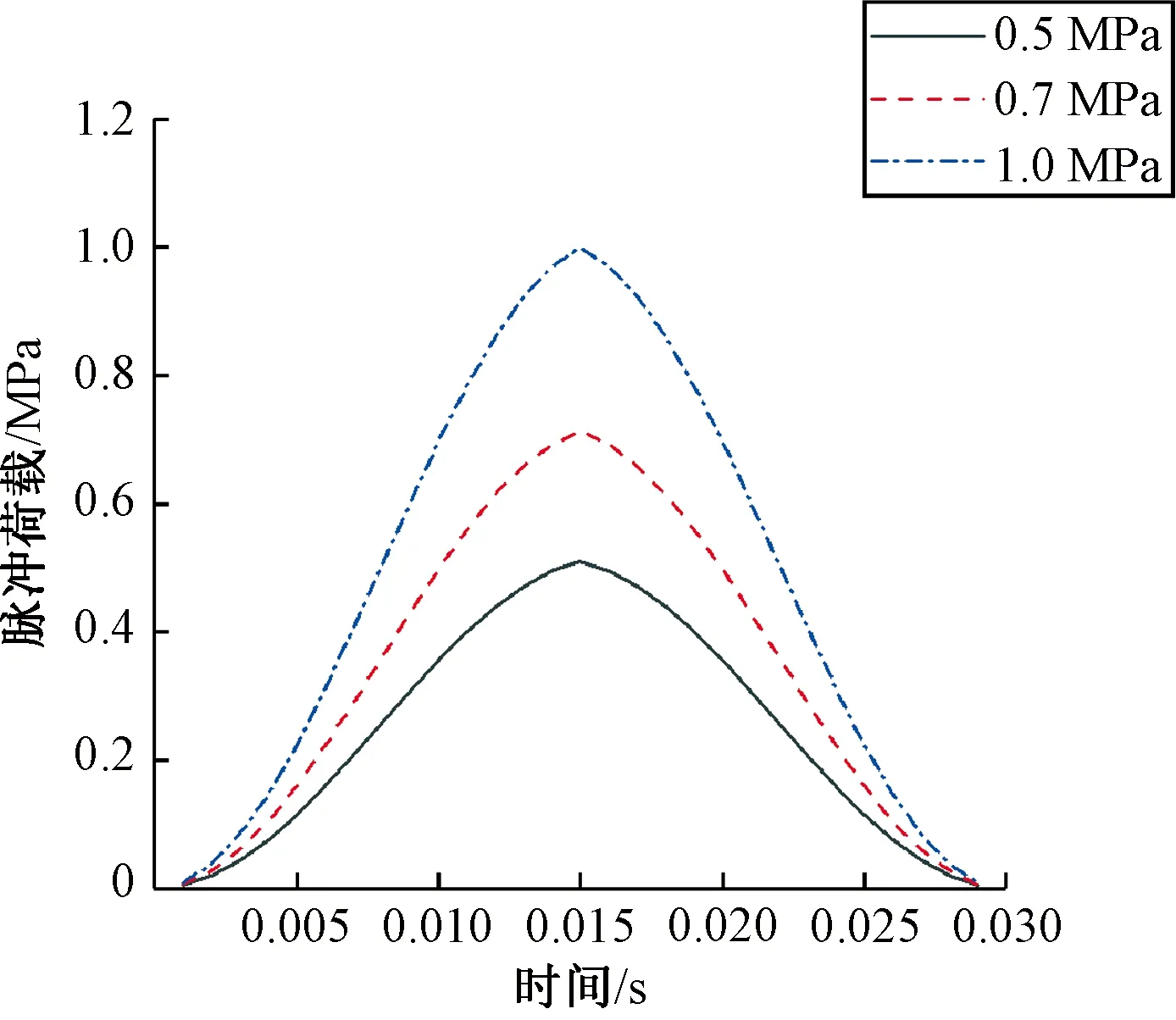
图3 脉冲荷载幅值Figure 3 The amplitude of impulse load

1.4 流场模型

在Fluent中建立三维流场模型，流场计算域为混凝土排水管道的内部圆柱形区域，直径为0.8 m，总长为11.9 m。通过ANSYS Workbench DesignModel建立流场几何模型，并利用ICEM CFD为流场域划分六面体结构网格，网格划分整体图如图4所示。

图4 流场网格Figure 4 The mesh of flow field

考虑到本次模拟的实际情况，设置流场为VOF(volume of fluid)多相流流动模型，其较适合本次模拟中管道内的气水分层流动。由于管道内流动情况较为复杂，根据张土乔等[10]的研究结果，RNGk-ε模型比较适合于无压圆管计算，具有精度高、计算量适中的优点，因此本次模拟选用RNGk-ε模型。

本次模拟计算涉及的边界条件如下：①水流进口，设置为速度进口。依照相关规范[11]，本次模拟流速设定为2.5 m/s，充满度设置为0.3、0.5、0.7；②空气进口，流域上部空气与大气连通，流动情况未知，设置压力值为0的压力出口；③出口边界，同上采用压力值为0的压力出口；④壁面条件采用无滑移壁面，并且因为RNGk-ε模型是高雷诺系数的湍流模型，所以选用了标准函数壁面法来模拟管道近壁面的流动情况。

1.5 流固耦合平台MpCCI

MpCCI是一款面向多学科、多物理场的专业耦合接口软件，也允许在多物理场中的两个仿真代码的网格之间交换力和位移等物理量。

由于结构和流场一般在耦合区域处的网格通常是不匹配的，二者网格的单元形状和节点位置并不是完全对应的，所以MpCCI采用的数据交换步骤主要包括以下3个方面。

(1)预接触搜索：在为流场和结构的对应网格接触搜索前，先将同类型网格分类以便下一步的操作。

(2)关联：对于耦合区域的每一个网格的每个节点或单元，必须找到对应区域的网格单元，然后，数据将在相关的单元或节点交换，这个过程也称为邻域搜索。

(3)插值：在已经关联的单元或节点之间将要传递的数据进行交换。

MpCCI流固耦合模拟的步骤如图5所示。

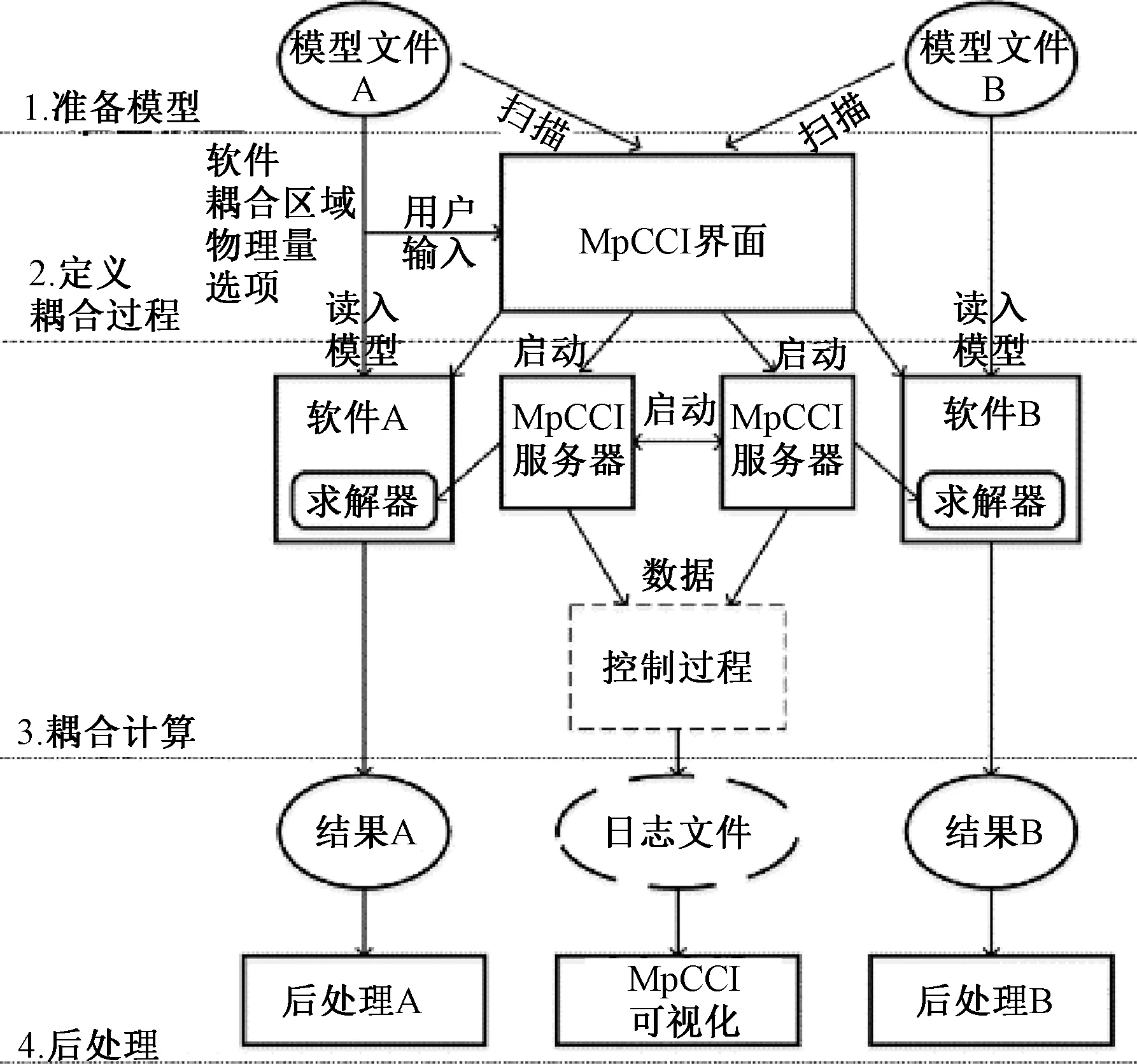
图5 MpCCI耦合计算流程Figure 5 The coupled calculation process of MpCCI

2 数值结果

本次模拟对比分析了不同流量、脉冲荷载幅值及作用位置对管道承插口力学性能和变形特性的影响。选取J3承插口为研究对象，沿其环向路径提取应力分布曲线，同时沿管道纵向长度提取管底竖向位移分布曲线，并且在文中定义了转角和剪切位移，如图6所示，其中转角是相邻管两节道绕管节转动的角度之和,即θL+θF，剪切位移δ是相邻承口端和插口端竖向位移差。

图6 转角和剪切位移示意图Figure 6 Joint rotation and shear displacement

2.1 管道流量对比

本节脉冲荷载峰值取0.7 MPa，作用在管节3的正上方。在3种不同的管道流体充满度(0.3、0.5、0.7)下承插口最大主应力和管底纵向路径竖向位移如图7和图8所示。

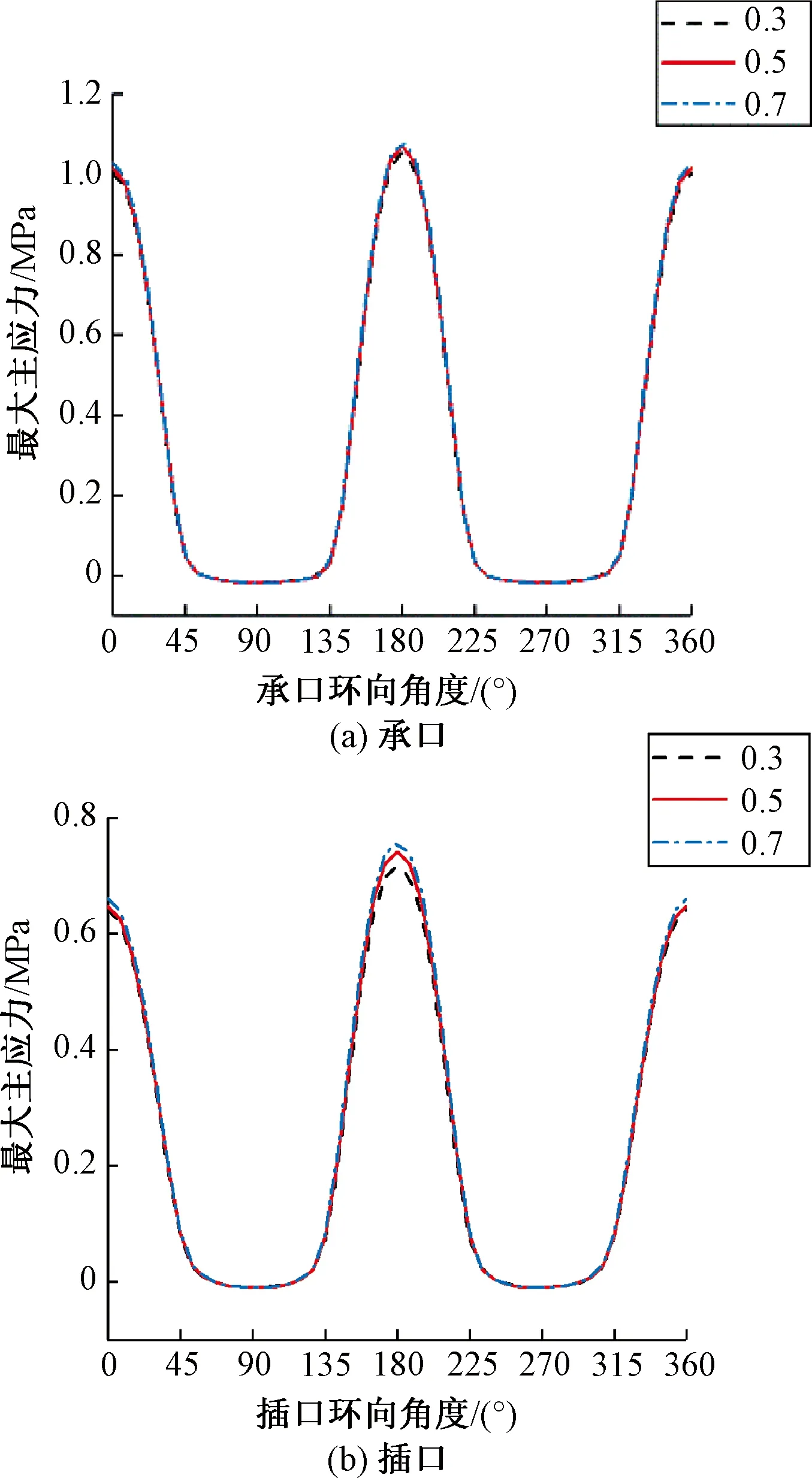
图7 不同流量承口、插口环向最大主应力对比曲线Figure 7 Comparison of the maximum principal stress of the bell and spigot under different flow rates

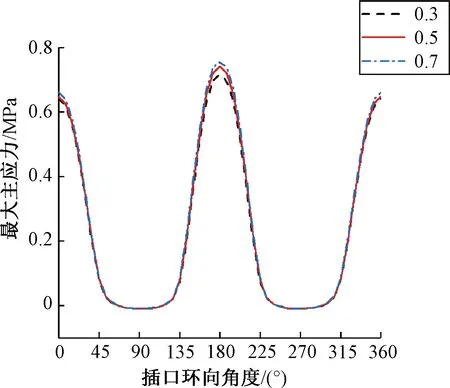
图8 不同流量管底竖向位移对比曲线Figure 8 Comparison of vertical displacement of the invert under different flow rates

从图7可以看出，在交通荷载和运行荷载耦合作用下，承插口的最大主应力分布曲线有明显的波峰和波谷，最大拉应力出现在管顶(0°)和管底(180°)，管肩和管臀(45°～135°、225°～315°)出现极小的压应力，管侧(90°、270°)的最大主应力最小。对比承口最大主应力分布发现，插口管顶和管底的应力峰值均小于承口。此外，随流量的增大，承插口环向最大主应力变化十分微弱，说明流量的增大基本不影响承插口的应力分布规律。

从图8可以看出，管底纵向路径竖向位移分布呈“中间低，两边高”的趋势，最大转角和剪切位移发生在J3处。随着流量的增大，管底竖向位移分布规律不受影响，但竖向位移值明显增加,而管节的转角值则几乎不受流量改变的影响。

2.2 交通荷载大小对比

本节交通荷载作用在管节3的正上方，管道充满度为0.5，在3种不同幅值大小的脉冲荷载(0.5 MPa、0.7 MPa、1.0 MPa)作用下，J3处承插口应力和管底竖向位移分布曲线如图9和图10所示。

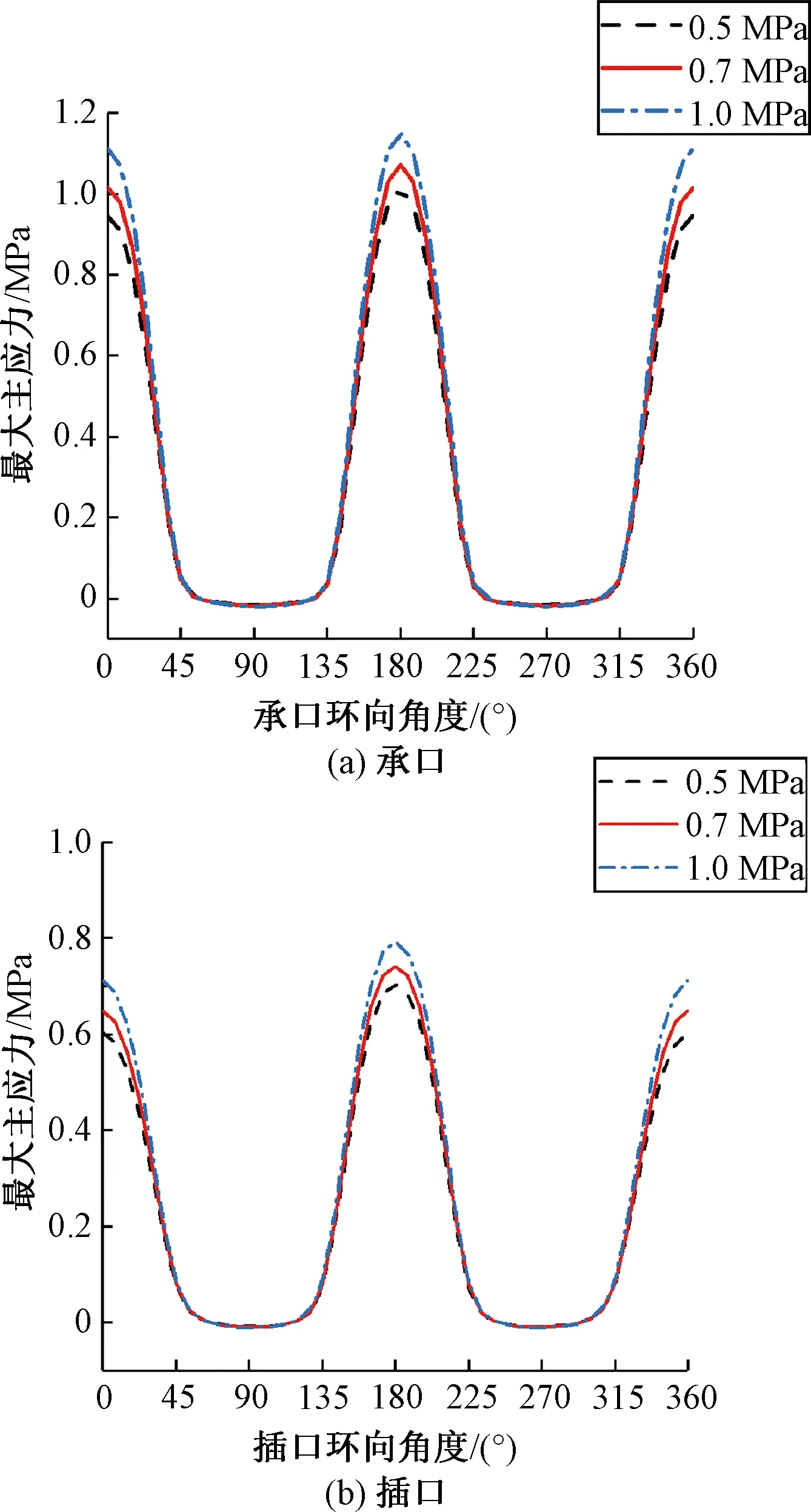
图9 不同荷载大小承口、插口环向最大主应力对比曲线Figure 9 Comparison of the maximum principal stress of the bell and spigotof different load amplitudes

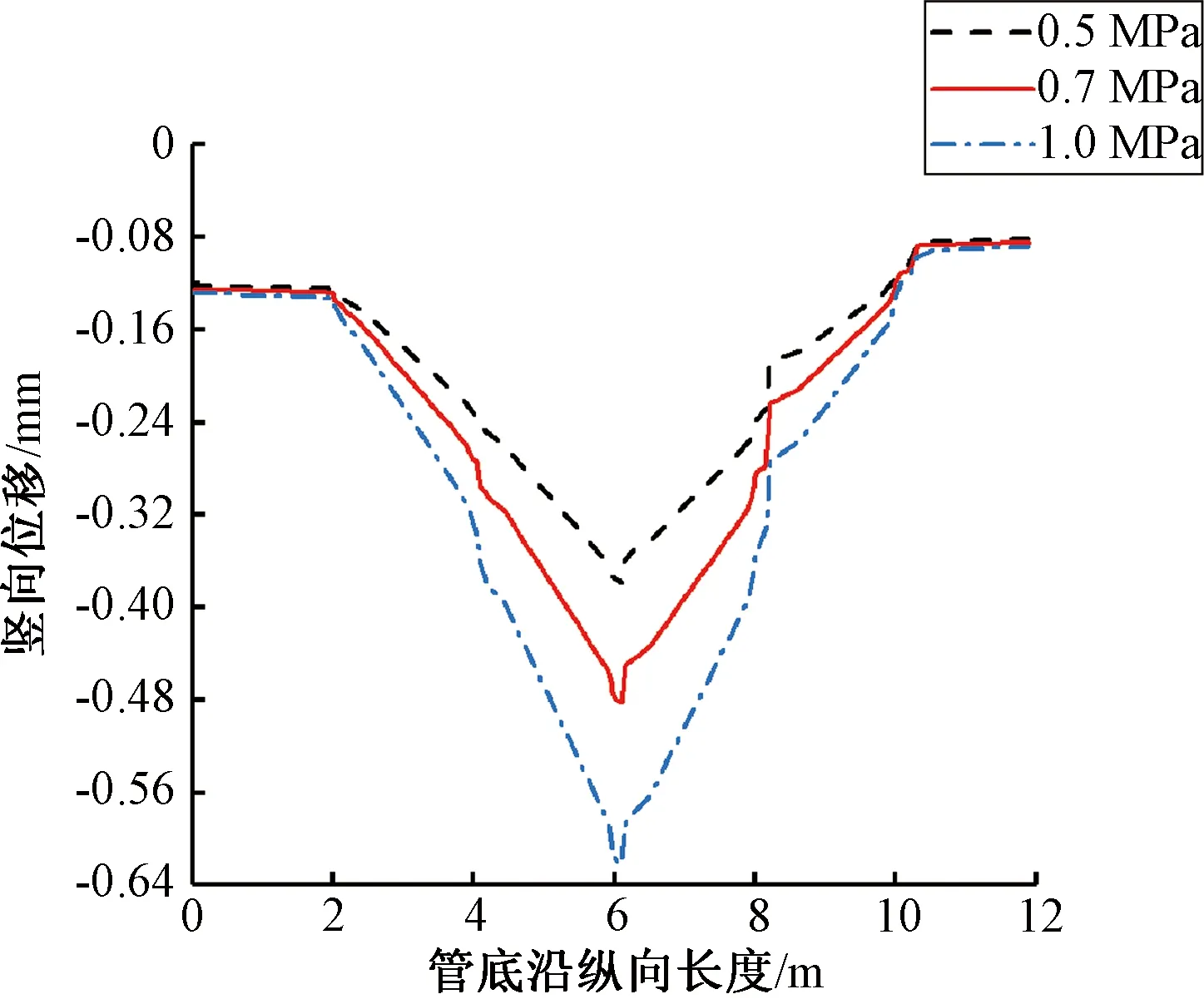
图10 不同荷载大小管底竖向位移对比曲线Figure 10 Comparison of vertical displacement of the invert of different load amplitudes

从图9可以看出，随着交通荷载的增大，承插口管顶和管底的最大主应力明显增加，管顶和管底的增幅最大，而其他部位的增幅较小，说明交通荷载大小的改变不影响承插口最大主应力的分布规律，但对管顶和管底的应力有显著影响。

从图10可以看出，竖向位移随交通荷载的增大明显增加，J3处承插口增幅最为显著。此外，各管节的剪切位移和转角均随交通荷载的增大而增加，J3处的转角增值最大，但剪切位移的最大增值发生在J2处，推测是由于承插口结构不对称造成的。

2.3 交通荷载作用位置对比

本节脉冲荷载作用位置在管节J3的基础上，向左和向右各移动1.0 m，如图11所示，荷载大小为0.7 MPa，管道充满度为0.5。图12和图13为不同交通荷载作用位置下J3处承插口应力和管底纵向路径竖向位移分布曲线。

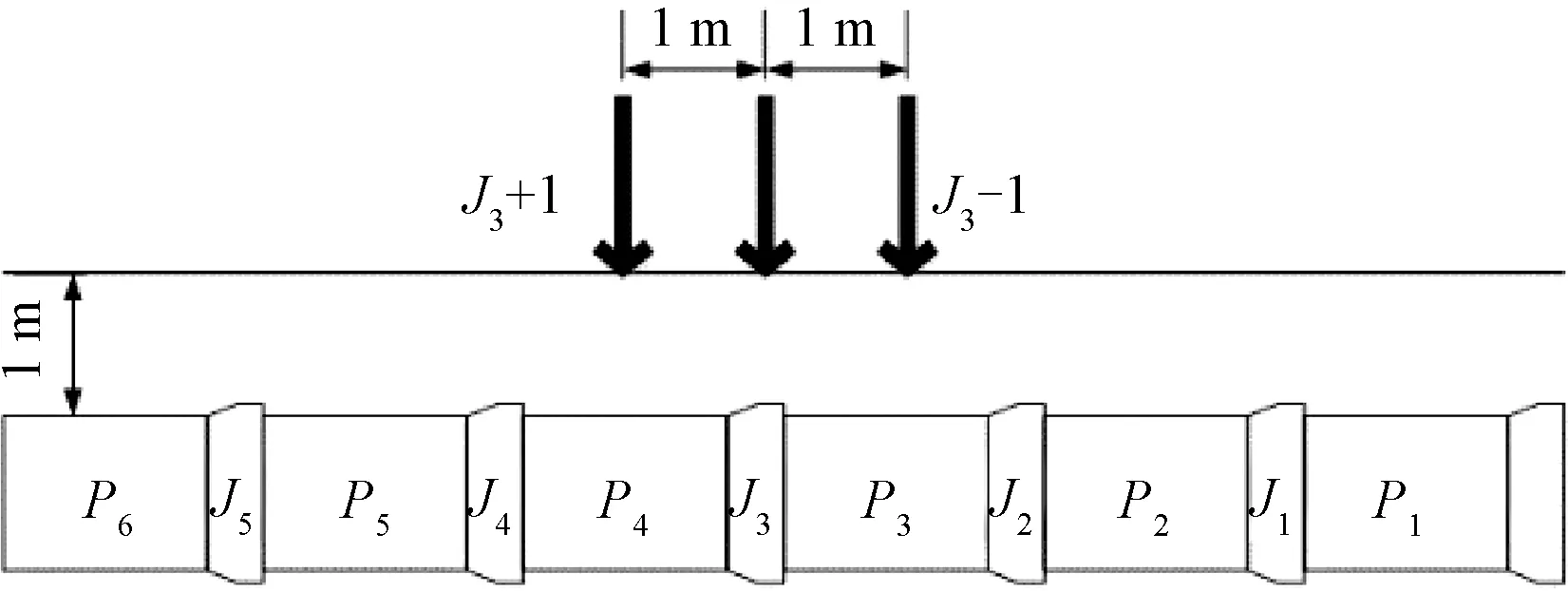
图11 荷载作用位置示意图Figure 11 Schematic diagram of the locations of the traffic load

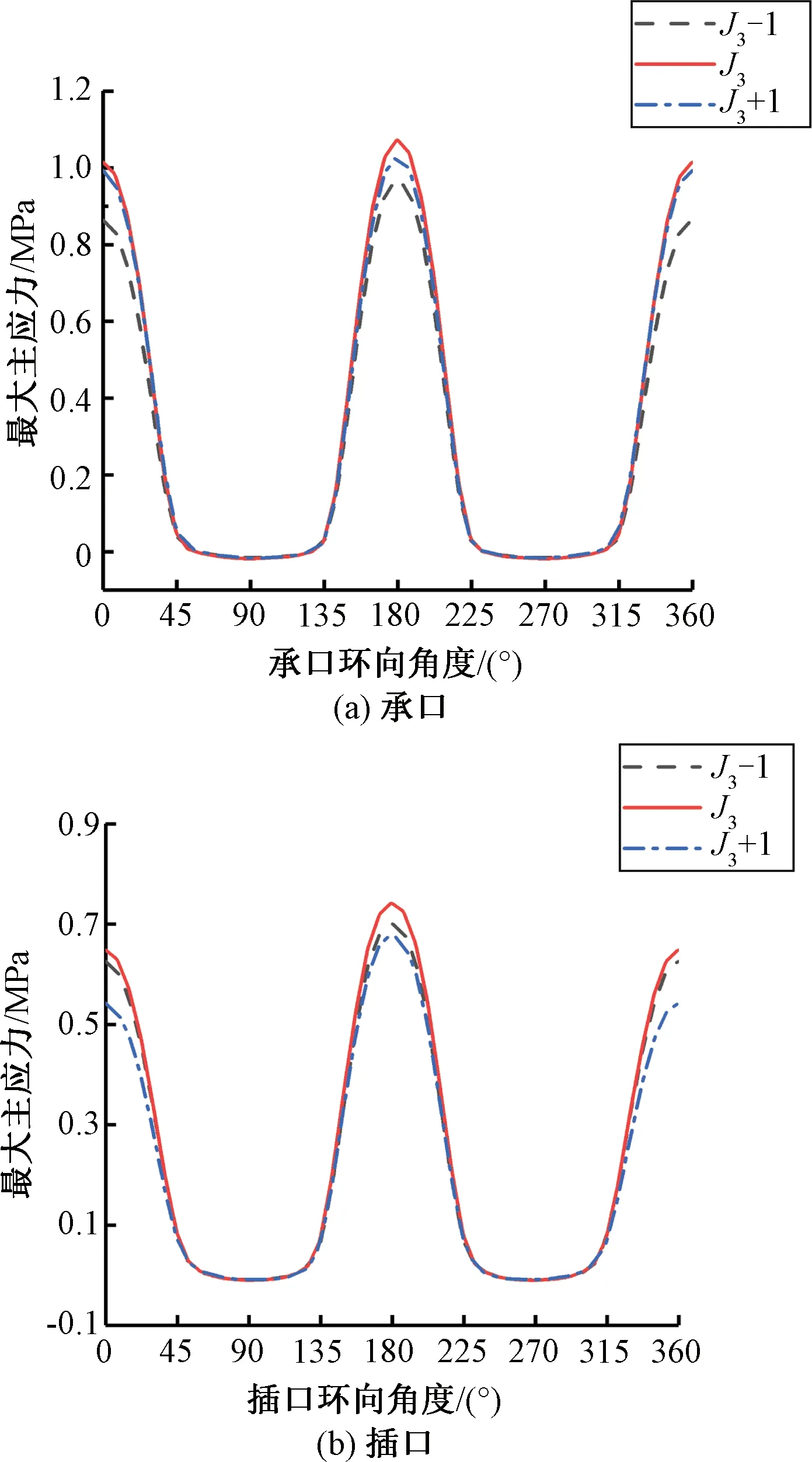
图12 不同荷载作用位置承口、插口环向最大主应力对比曲线Figure 12 Comparison of the maximum principal stress of the bell and spigotunder different load positions

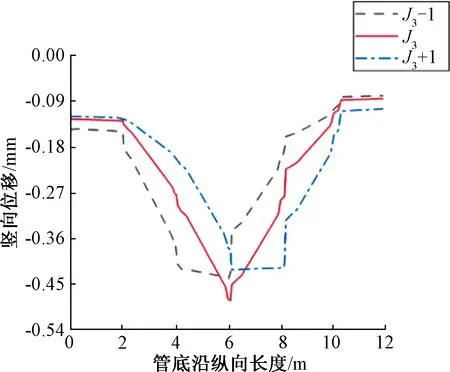
图13 不同荷载作用位置管底竖向位移对比曲线Figure 13 Comparison of the maximum principal stress of the invertunder different load positions

从图12可以看出，交通荷载位置的改变并不影响承插口最大主应力分布规律，但管顶和管底的拉应力峰值有微弱变化。当荷载作用在J3时，承插口的管顶和管底的最大主应力峰值稍大于其他工况，说明荷载作用在管节正上方对承插口动力响应的作用更显著。

从图13可以看出，交通荷载作用位置的改变对管底竖向位移的分布规律和数值均有显著影响，荷载作用在J3处时，管底竖向位移达到峰值。当交通荷载作用在J3+1和J3-1位置时，中央管节的转角均小于J3位置的转角，但中央管节的剪切位移均大于J3位置的剪切位移，亦说明交通荷载作用的改变对承插口动力响应的作用更显著。

3 结论

利用多种软件实现了埋地混凝土管道在多物理场耦合作用下的数值研究，得到以下结论:

(1) 在交通和运行荷载耦合作用下，承插口的管顶和管底两侧各45°范围受拉，且管底和管顶的拉应力值明显较大，容易受到破坏。此外插口的应力值略小于承口，因此，承口部位最易受拉损坏。

(2)承插口环向最大主应力以及管道沿程的竖向位移均随流量的增大而线性增加，但影响较小。

(3) 承插口环向最大主应力和管底竖向位移随交通荷载的增大呈显著线性增加趋势，承插口最大主应力及管底竖向位移峰值出现在J3处，表明交通荷载作用在管节正上方时对管道受力有较大影响。

(4)当荷载作用于J3管节处时，承插口的最大主应力、管道沿程竖向位移及管节转角达到峰值，而管节的剪切位移在荷载作用于管身时达到峰值。