钢管塔结构强度的有限元分析及试验研究
2020-10-12耿景都苏志钢王璋奇
王 孟, 耿景都, 苏志钢, 王璋奇
(1.华北电力大学 能源动力与机械工程学院, 河北 保定 071003; 2.中国电力科学研究院,北京 102401)
0 引 言
在利用有限元方法分析特高压输电铁塔力学特性时,选择合理有效的力学分析模型是关键。传统的铁塔结构分析都将其简化成平面/空间桁架结构,目前输电铁塔的设计规范也是以此模型为基础制定的。铁塔的桁架模型简单实用,但却常常会出现平面节点的问题,需要特别处理,文献[1,2]提出了角钢塔的桁梁混合建模的观点,并对铁塔主材、横隔材、斜材、辅助材的受力特点进行分析。现有的铁塔结构分析工作多以ANSYS为计算工具[3-5],直接将铁塔简化成“刚架”模型进行分析,甚至把辅助材都简化成梁单元,这不仅与铁塔是采用螺栓连接的事实严重不符,也与某些细长杆件仅承受轴向拉压力的客观情况偏差较大。这不仅增加了铁塔分析计算的工作量,而且也给计算结果带来了“额外”的不合理因素。因此,有必要针对铁塔建模问题,尤其是在新型的特高压钢管塔结构分析方面,开展进一步的建模与分析理论研究。文献[6]以塔线系统为基础,讨论钢管塔设计的计算模型选择问题,文献[7-10]采用有限元分析方法研究了钢管塔法兰的力学特性,计算结果表明钢管节点抗弯刚度对钢管塔主材受力有一定的影响。文献[11]对铁塔试验的失效原因进行了分析。文献[12]采用有限元方法研究了适应于城区线路建设的新型窄基钢管塔结构的振动特性。文献[13]通过1 000 kV特高压钢管塔的真型试验研究了钢管塔的局部屈服。
本文以国内设计的1 000 kV线路用某特高压钢管塔为研究对象,考虑到特高压钢管塔所采用的“钢管”与传统铁塔用的“角钢”之间的受力特性差异,提出特高压钢管塔的桁梁混合模型的建模原则与方法,建立了某特高压钢管塔的桁梁有限元模型,计算典型工况下杆件受力和变形,并与真型塔的试验结果进行了分析与对比,验证特高压钢管塔的桁梁混合模型的有效性,加深了对特高压钢管塔受力特性的认识和理解,为特高压钢管塔的结构设计、优化选材、可靠性分析等提供理论基础。
1 特高压钢管塔的有限元建模
1.1 特高压钢管塔构件受力特性分析
一般来说,高压输电铁塔角钢杆件主要承受的是轴向拉压力,不能承受剪力和弯矩,并在各杆件连接处多采用普通螺栓联接,因此在工程分析和计算中,人们倾向于将铁塔视为平面/空间桁架模型进行分析计算,并基于此计算模型,研制了输电铁塔结构设计软件[1]。特高压钢管塔一般选用钢管材料代替传统铁塔的角钢材料,使其构件的受力特性得到了极大地改善,避免了角钢铁塔中杆件偏心拉压的问题,大大地提高了单个构件的承载能力。更进一步地,特高压钢管塔的主材是通过法兰“对接”,杆件的同心度高,且具有一定的抵抗剪切变形的能力,也提高了铁塔结构的整体承载力,典型的特高压钢管塔节点如图1所示。

图1 特高压钢管塔局部杆件及节点Fig.1 Local members and joints of UHV steel tubular tower
在特高压钢管塔受力分析过程中,如何合理地考虑主材既能承受较大轴向力又能够承受一定的横向剪切力的受力特点,值得深入研究。
由图1的特高压钢管塔结构图可看出,主材钢管直径远大于斜材直径,相对于斜材而言,主材在节点处的抗弯刚度是比较大的,在计算模型中考虑抗弯刚度的影响是必要的。特高压钢管塔的桁梁混合模型建模方法,是将钢管塔的主材、横隔材等简化成“梁”单元,而将斜材等简化成“杆”单元,辅助材是铁塔构造所需要的,一般不承受载荷,属于杆系结构受力分析中的“零杆”,故可不参加受力分析模型的计算。这样得到的铁塔有限元分析模型不仅能更好地反映实际的钢管塔结构中各类杆件的受力特点,而且还能有效地避免铁塔的简单桁架模型中不易解决的平面节点问题[1, 2]。
在建立钢管塔结构分析的有限元模型时,首先需要对整个钢管塔的结构进行离散化处理。以钢管塔杆件的截面几何中心线为基准,任意两条相交的中心线处形成计算模型的节点;节点将杆件离散形成单元,单元的物理参数由构件材料的截面特性所确定。将既能承受轴向拉压力又能承受横向剪力和弯矩的主材和横隔材简化成梁单元,主要承受轴向拉压力的斜材则简化成杆单元。构造所需,但不受力的辅助材则被忽略掉,不参与有限元模型的计算,在杆塔设计规范中,这类不受力的辅助材是按照“所连接主材受力的2%”来选材料规格的。在钢管塔的有限元模型中,辅助材不作为计算模型中的单元,辅助材与其它单元的连接处也无需离散成节点,也就是说主材、斜材单元与辅材的连接处无需离散,但辅助材的自重和外载荷需要用静力等效的方法移置到相应的梁节点上。
根据钢管塔中各类杆件的受力特点,可以将特高压钢管塔离散成一个桁梁混合的有限元模型。该模型将主材简化成梁单元,组成特高压钢管塔有限元模型的“主结构”,“主结构”本身具有承载能力;将斜材简化成杆单元,填充到“主结构”中去,对“主结构”杆件起到支撑和加强的作用。这样建立的特高压钢管塔有限元分析模型可充分反映各杆件受力特征,并与钢管塔的设计理念相一致。
基于上述分析的特高压钢管塔建模准则,所建立的钢管塔的桁梁混合有限元计算模型,具有如下的特点:
(1)特高压钢管塔离散成的桁梁混合有限元模型中包括梁单元和杆单元两类单元。
(2)先将特高压钢管塔的主材(包括横隔材)离散成梁单元,构成钢管塔有限元模型的“主结构”,再将斜材离散成杆单元填充到“主结构”中。
(3)特高压钢管塔有限元模型中的所有节点,都处于主材或横隔材上,即有限元模型的梁单元之上。
(4)特高压钢管塔有限元模型的计算边界条件为:钢管塔4个塔脚点在空间坐标系下三个方向上的位移全部被约束。
1.2 某1 000 kV特高压钢管塔的有限元模型
1 000 kV淮南-上海(皖电东送)输变电工程是国内第一条特高压双回路交流输变电工程。该输电线路具有输送容量大,全线杆塔均采用钢管塔结构,在国内尚属首次。钢管塔中的钢管连接采用了工厂化的锻造法兰、十字形插板、U型插板、槽型插板等新技术和新工艺。图2是某1 000 kV双回钢管转角塔的单线图,主要设计参数见表1所示。
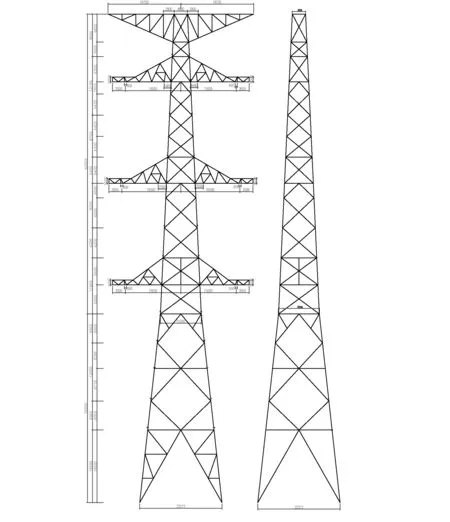
图2 特高压钢管塔单线图Fig.2 Single line drawing of UHV steel tubular tower

表1 特高压钢管塔基本参数Tab.1 Basic parameters of UHV steel tubular tower
该特高压钢管塔使用了22种钢管规格及一种角钢规格,材料为Q345和Q235两种。
该特高压钢管塔对称结构,按对称面可以将整个塔分为四部分,分别对应xoy平面坐标系上的四个象限。在建立有限元模型的节点时,首先生成位于其中一个象限内的节点,然后通过两步镜像操作生成剩余三个象限上的节点。节点生成后再通过节点构建模型的单元,给单元赋予相应的截面属性参数,这样就得到完整的具有对称特征的特高压钢管塔的有限元模型。
采用上述方法得到的特高压钢管塔有限元模型,可以充分保证计算模型的对称性,为后续判断钢管塔有限元计算结果的正确性提供方便。据此建立的某1 000 kV输电线路某双回转角钢管塔的有限元模型如图3所示。图3(a)为由主材和横隔材离散成的梁单元组成的“主结构”;图3(b)为填充起支撑作用(斜材)杆单元后得到的钢管塔有限元计算模型。
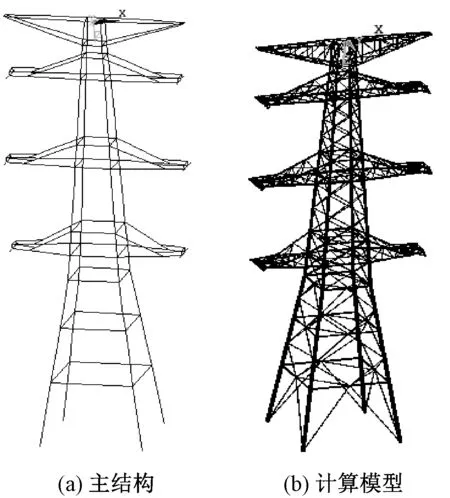
图3 特高压钢管塔有限元模型Fig.3 Finite element model of UHV steel tubular tower
1.3 特高压钢管塔有限元模型的验证
为了验证所建模型的合理性,选取特定载荷工况,计算所建特高压钢管塔的桁梁混合模型的杆件内力和变形,通过对计算结果的分析对比,来验证该有限元模型的合理性。
(1)自重加载工况:考虑到模型的对称性,给塔模型施加自重载荷,计算得到各杆件的内力,4个塔腿主材的计算结果见表2。结果显示:各节间主材的内力分别相等,且内力合成结果恰好等于该节以上铁塔的自重;对应位置斜材的内力数值也相等,符合对称的规则。
(2)水平加载工况:在铁塔顶部的右横担的两角点上分别施加50.0 kN的横向水平拉力,不考虑自重,考察铁塔整体处于侧向弯曲状态,塔腿部主材内力计算结果见表2。计算结果表明:铁塔的四根主材中内力数值相等;载荷所在右侧面主材、交叉斜材承受压力,而相对左侧的主材、交叉斜材承受等值的拉力;塔前后两面的交叉斜材分别受到数值相等的拉力或压力。符合对称性的规律,且数值完全相等。

表2 塔腿主材内力Tab.2 Inner forces of leg members (kN)
由此可见,采用本文提出的钢管塔有限元建模方法,所获得的有限元模型,可以反映铁塔构件的受力特征和规律。
2 特高压钢管塔的有限元计算
2.1 分析计算工况的选择
铁塔真型塔试验是检验铁塔结构合理性的最直接有效的方法[8,9]。本文研究的特高压钢管塔应用于1 000 kV淮南-上海(皖电东送)输变电工程,为保证其可靠性,开展了真型塔试验研究。试验工况共有30余种,本文仅选择两种典型的控制工况,横向载荷较大的大风工况和垂直载荷最大的覆冰与正常风组合工况(以下称为组合工况)进行分析。
输电铁塔的真型试验过程中,首先依据设计规范计算各工况下的铁塔载荷值,然后根据试验站的加载条件,将载荷分多个“加载步”通过牵拉钢丝绳施加于全尺寸真型铁塔,直至最大载荷。加载的同时,由测量系统同步测量钢管塔各主要构件的受力及节点位移,输电铁塔真型塔的加载和试验情况如图4所示。

图4 真型塔试验现场Fig.4 Full- scale load test site
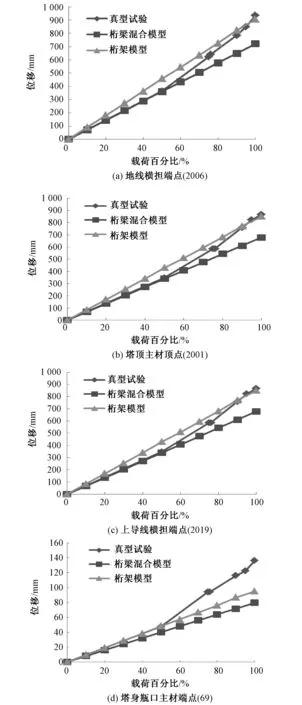
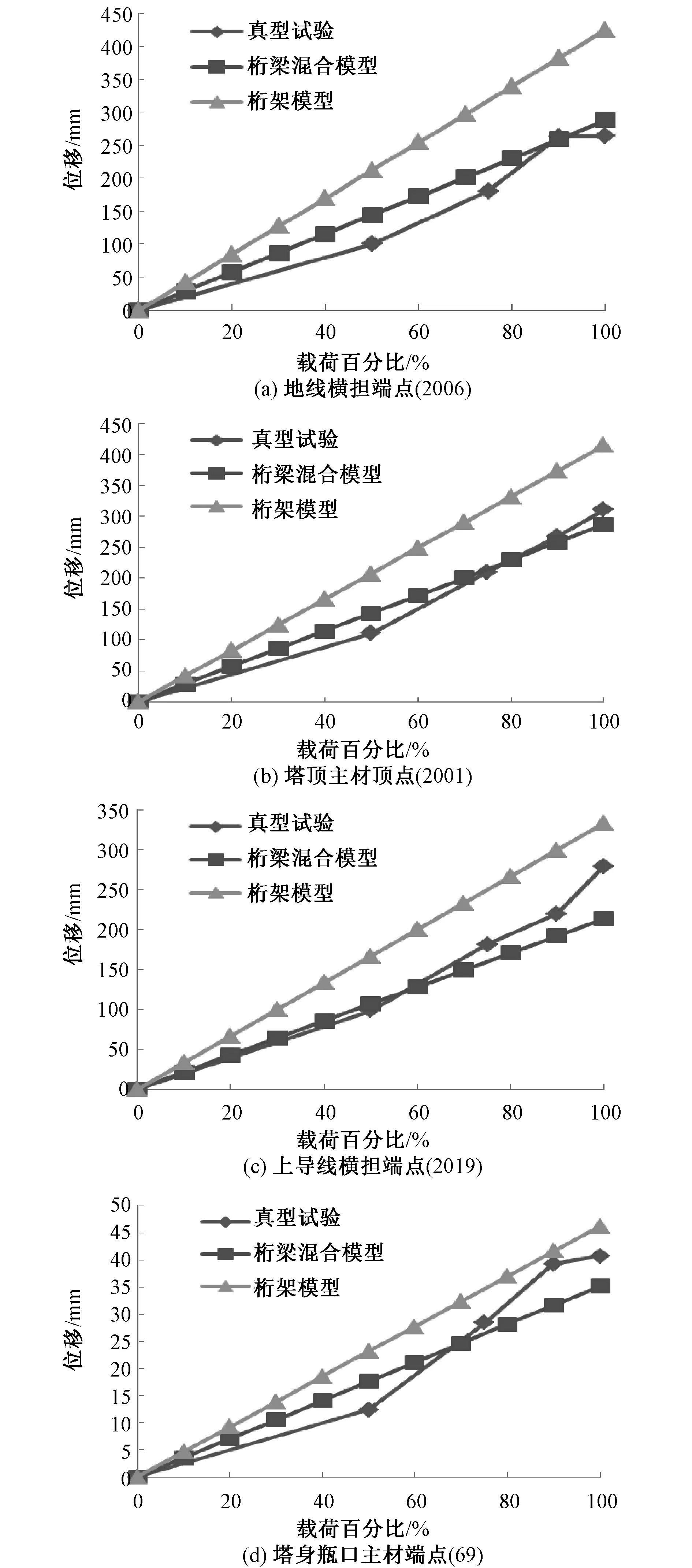
典型特高压钢管塔有限元模型,以及加载情况如图5所示。

图5 真型塔试验载荷图Fig.5 Load conditions for full- scale load test
有限元模拟分析计算过程与真型塔试验的加载过程保持一致,分若干“加载步”(10步)进行计算,得到各步加载后的杆件受力和节点位移的计算结果。
2.2 大风工况计算结果
通过有限元模型的计算,大风工况下特高压钢管塔的应力云图和位移云图如图6所示。
从图6看出,大风工况下的塔身构件有两处应力较大的区域,塔身的最大拉应力出现在瓶口以下第二节间的左后侧塔身主材(图6(c)),其值为148 MPa,该构件采用Q345材料,材料的抗拉强度设计值为310 MPa,148 MPa 图6 大风工况的应力及位移Fig.6 Stress and displacement under wind condition 除了需要满足上述强度破坏条件,还应考虑钢管塔构件的稳定性问题。与强度破坏不同,稳定性问题与塔材的长细比有关,越细长的构件越容易失稳。塔腿主材为梁单元,除受轴向力作用外,还受剪力、弯矩的作用,但剪力与轴力相比较小,在考虑梁单元的稳定性时可忽略剪力的影响。由设计规范可知,对于压弯构件需满足下式即可认为满足稳定性条件要求: (1) 式中:f为钢材抗压强度设计值,MPa;N为轴向压力值,N;M为弯矩值,N·m;A为构件横截面积,mm2;φ为轴向受压构件稳定性系数;mN为压杆稳定强度折减系数;mM为受弯构件稳定强度折减系数;W为构件抗弯截面系数,mm3。 轴向受压构件稳定性系数φ由材料、截面分类和长细比确定,压杆稳定强度折减系数mN和受弯构件稳定强度折减系数mM对于该铁塔皆取1.0。该构件的N=2 239 900 N,M=7 396 N·m,φ=0.93,W=1.077 6×10-3m3,将这些参数代入(1)式,得到该单元的计算应力值为236 MPa,以此值作为该单元的应力判断值,236 MPa 在最大覆冰和大风组合工况下,计算得到的钢管塔杆件应力和变形情况如图7所示。 由图7(c)看出,组合工况下的最大拉应力出现在左下导线横担上部主材,其值为199 MPa,该构件材料是Q345,199 MPa 图7 组合工况的应力及位移 Fig.7 Stress and displacement under combined loads 针对1 000 kV特高压钢管塔分别用本文的桁梁混合有限元模型和普通的桁架有限元模型进行了详细的分析计算,并对两种模型的计算结果与真型塔试验的结果进行分析对比。整体来看,桁梁混合模型的计算结果与试验结果的一致性更好些。现从铁塔结构中选取4个典型节点和3个典型受力构件(如图8所示)予以说明,典型节点的位移和典型杆件受力的分析对比如下。 图8 铁塔模型上的典型节点和塔材Fig.8 Typical joints and tower members 选择铁塔模型上的典型节点有地线横担端点、塔顶主材顶点、上导线横担端点、塔身瓶口主材等(图8(a)),提取这4个典型位置的节点位移结果,并与塔真型试验测得的位移数据进行比较,大风工况和组合工况下的节点位移对比情况分别如图9和图10所示。 图9 大风工况下典型节点位移Fig.9 Displacements of typical nodes under wind condition 图10 组合工况典型节点位移Fig.10 Displacements of typical nodes under combined loads 从图9和图10可以看出: (1)桁梁混合模型和桁架模型的各节点位移值都与荷载成线性关系。在不考虑材料和实际铁塔中存在节点滑移等非线性效应的情况下,铁塔结构的变形及内力与铁塔的载荷保持线性关系。铁塔真型试验得到的位移-载荷曲线表明:在加载50%之前载荷-位移曲线基本保持线性关系,此后则表现出明显的非线性特性,位移增加的速度明显加快,一般认为这是节点滑移所致。尽管如此,两种有限元分析模型的计算结果与铁塔真型试验结果的一致性还是比较好的,相对误差符合试验要求。 (2)在两个工况下,桁架模型位移值都比桁梁混合模型的位移值略大,且都略大于铁塔真型试验测得的位移值。这是因为桁架模型忽略了主材杆件抗弯的能力、横隔材的抗弯刚度等所致。 从两种计算模型的轴力数据中提取1 381、79、115、1 306这4个单元的轴力,单元的位置如图8(b)所示,单元1 381为塔腿斜材,单元79为下导线横担上部主材,单元115为中导线横担处的塔身主材,单元1 306为塔身瓶口处主材。 通过真型试验数据计算得到4个单元的轴力值,并与两种有限元模型计算得到的轴力一起,绘制钢管塔杆件的轴力-荷载曲线图,见图11和图12。 图11 大风工况典型杆件的轴力Fig.11 Axial forces in typical members under wind condition 图12 组合工况的典型杆件轴力Fig.12 Axial forces in typical members under combined load 由图11和图12可以看出: (1)桁梁混合模型、桁架模型计算的轴力值及真型塔试验得到的杆件轴力值,基本上都随载荷的增加而成线性变化; (2)在真型塔试验结果中,当载荷为零时,试验记录显示的轴力值不为0,这是其它工况产生的残余变形所致。考虑增量或者变化趋势(曲线的斜率),不难发现实验结果和钢管塔桁梁混合有限元模型的结果更符合一些。 分别用本文建立的特高压钢管塔桁梁混合有限元模型和桁架模型对1 000 kV特高压钢管塔进行了分析计算,并将计算结果与该特高压钢管塔的真型试验结果进行了对比分析,得到如下结论: (1)本文提出的特高压钢管塔桁梁混合有限元模型可以充分体现特高压钢管塔各类杆件的受力特点,是进行特高压钢管塔结构分析计算的有效模型。 (2)大风工况的最大拉应力出现在塔身瓶口以下第二节间的左后侧塔身主材,最大压应力出现在中导线横担处的塔身主材;覆冰工况的最大拉应力出现左下导线横担上部主材,最大压应力出现在左下导线横担处的下部主材。钢管塔桁架模型的分析计算结果与试验结果一致。 (3)钢管塔的桁架模型计算得到的节点位移值比其桁梁混合模型的位移值略大些,且桁梁混合有限元模型的计算结果更接近于真型塔的试验结果。 (4)钢管塔的桁架模型、桁梁混合模型所得到的杆件内力与真型塔试验结果一致性较好,但桁梁混合有限元模型所得到的杆件内力变化趋势与试验结果更接近。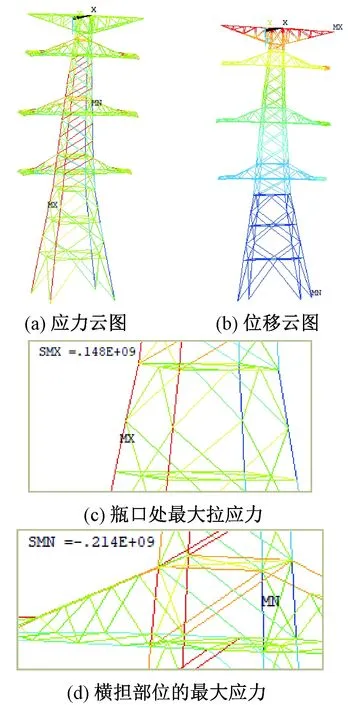
2.3 组合工况计算结果

3 有限元计算与真型塔试验结果对比
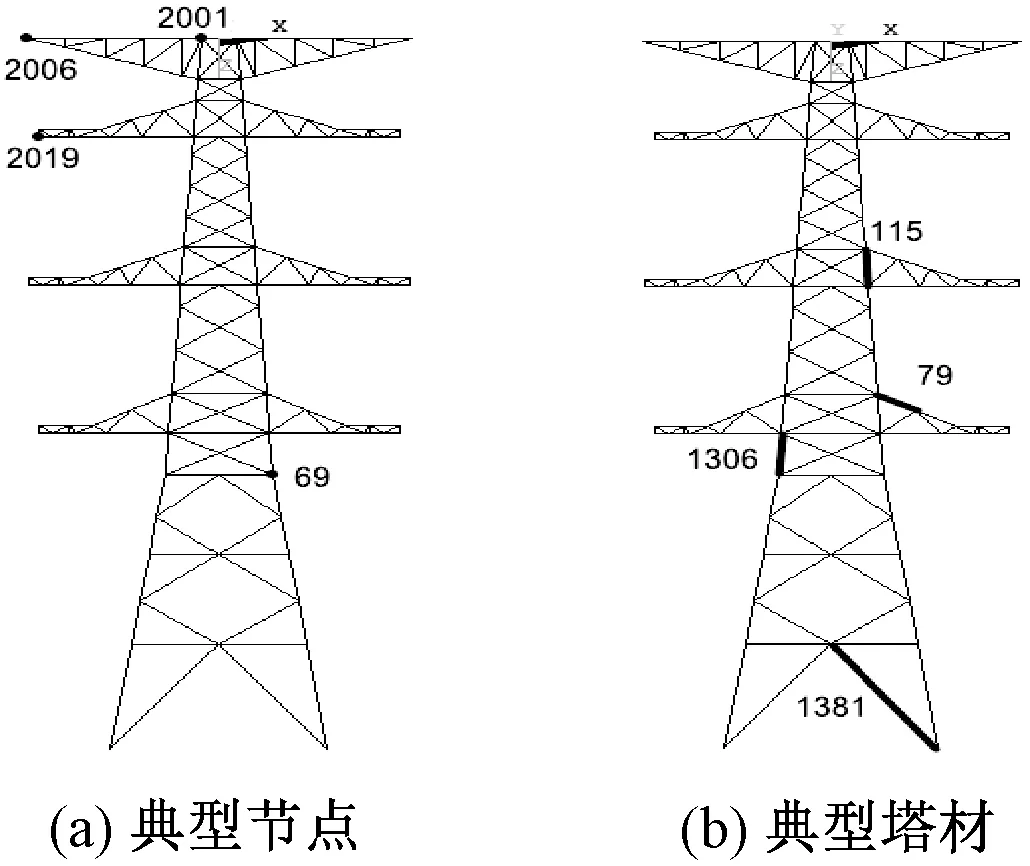
3.1 典型节点位移分析
3.2 典型杆件轴力分析


4 结 论
